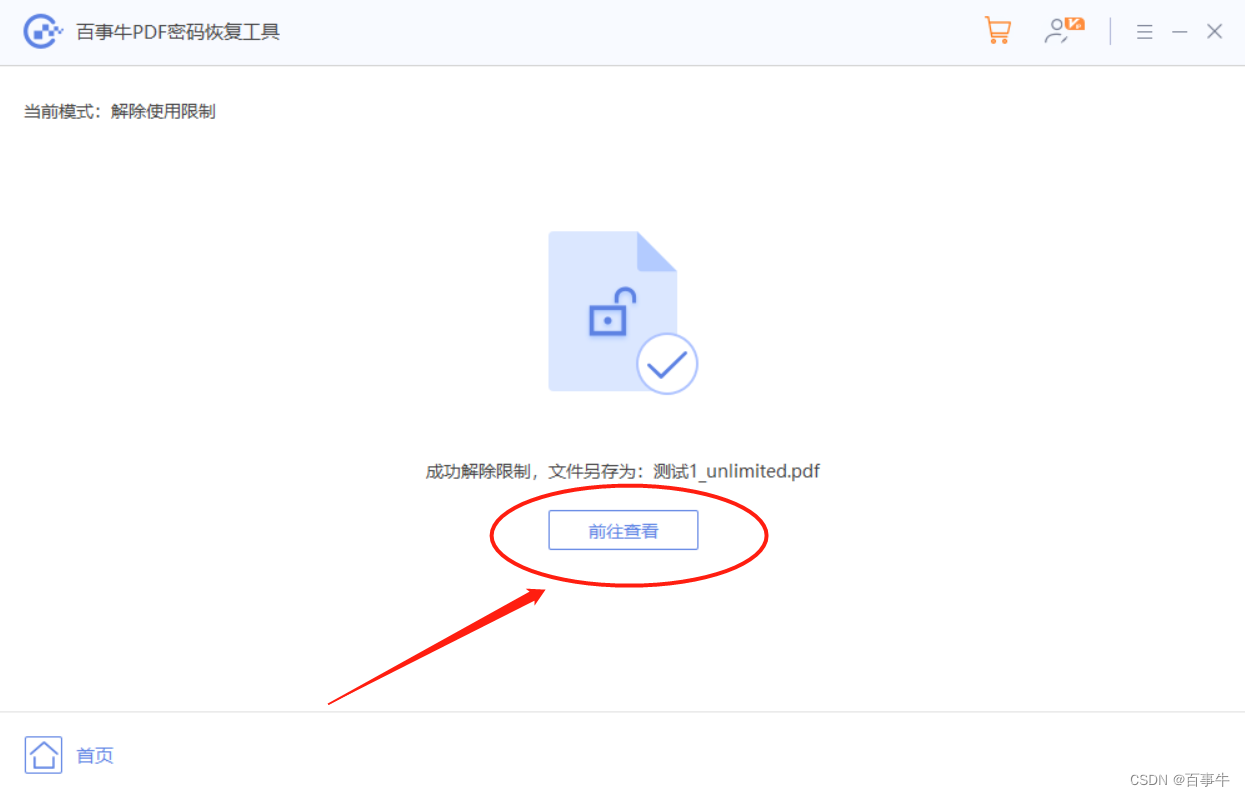
2D图形SVG工具添加了通过选项属性显示交点的功能。

PaladinDu：2D图形SVG化工具0 赞同 · 0 评论文章

在这个工具中，已经定义的数据结构有点，线段，有向线段，射线，直线，多边形，和圆。

其中点不参与交点检测；

线段，有向线段，射线，直线本质都是线段；

多边形由多个线段组成；

所以求交点的问题被减少为：

1.线段与线段；2.圆与圆；3.线段与圆求交点的问题。

线段与线段求交点

两个线段之间的关系可以分为以下几种：

不相交，相交且交点为端点，一般相交，相交且平行

由于工具默认显示线段的端点，对于 相交且平行 和 相交且交点为端点 的情况不在添加交点。

这样就只需要处理完全相交的情况，问题变得简单了许多。

这里用到的算法也比较简单，代码与流程解析如下：

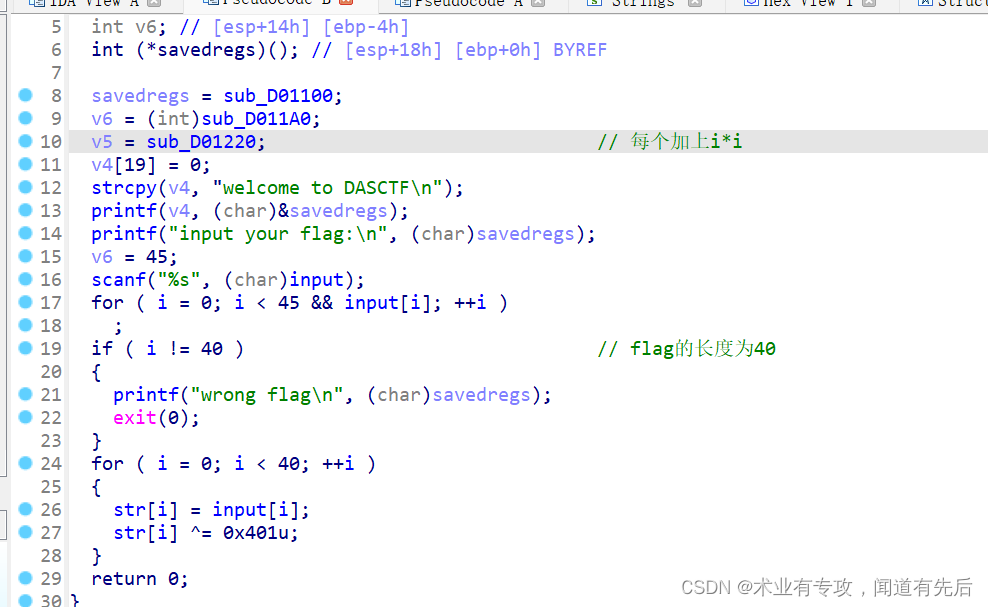
class LineSegment:
    def __init__(self,start:Position,end:Position):
        self.start = start
        self.end = end    

    def is_collision(self,other):  # 通过叉乘检测两个线段是否都满足端点在另一个线段的两侧
        self_dir = self.end.reduce(self.start)
        if self_dir.cross(other.start.reduce(self.start)) * self_dir.cross(other.end.reduce(self.start)) >=0:
            return False 
        other_dir = other.end.reduce(other.start)
        if other_dir.cross(self.start.reduce(other.start))*other_dir.cross(self.end.reduce(other.start)) >= 0:
            return False
        return True

def get_intersection_points_by_line_segments(line_segment1:LineSegment, line_segment2:LineSegment):
    if not line_segment1.check_aabb_by_other_obejct(line_segment2):  # aabb没有碰撞，直接返回
        return []
    if not line_segment1.is_collision(line_segment2):  # 通过叉乘检测线段是否为一般相交
        return []
    # 通过面积比例得出交点所在的位置
    line_segment2_dir = line_segment2.end.reduce(line_segment2.start)
    s1 = abs(line_segment2_dir .cross(line_segment1.start.reduce(line_segment2.start)))
    s2 = abs(line_segment2_dir .cross(line_segment1.end.reduce(line_segment2.end)))
    line_segment1_dir = line_segment1.end.reduce(line_segment1.start)
    return [line_segment1.start.add(line_segment1_dir .multiply(s1 / (s1 + s2)))]

圆与圆求交点

圆与圆之间的关系可以分为以下几种：

外侧不相交，包含不相交，包含一个点交点，包含圆心两个交点，外部一个交点，外部两个交点

不相交的情况可以通过两个圆心的距离与两个半径的和和差的大小比较过滤。

特殊的，对于重叠的圆，可以通过圆心相同排除。

对于一个交点的情况，可以直接通过两个圆的圆心向量信息得到交点：

需要注意的是，如果是内包的情况，选择较小的圆的圆心作为起始的需要将方向反转。

对于两个交点的情况使用了三角形三边求角度，然后旋转圆心向量的方式得到交点

两种情况的逻辑一致

代码与流程解析如下：

def get_intersection_points_by_circles(circle1:Circle,circle2:Circle):
    c1_to_c2_dir = circle2.center_pos.reduce(circle1.center_pos)
    center_pos_dif = c1_to_c2_dir.len()
    if center_pos_dif > circle2.r + circle1.r or center_pos_dif < abs(circle1.r-circle2.r):  # 内包或者距离过远了
        return []
    if center_pos_dif == 0:  # 圆心重叠了
        return []
    if center_pos_dif == circle2.r + circle1.r or center_pos_dif == abs(circle1.r-circle2.r):  # 只有一个交点的情况
        if center_pos_dif == abs(circle1.r-circle2.r) and circle1.r < circle2.r:  # 如果是内包且起始点为更小的圆，反向
            position = circle1.center_pos.reduce(c1_to_c2_dir.to_unit_dir().multiply(circle1.r))
        else:
            position = circle1.center_pos.add(c1_to_c2_dir.to_unit_dir().multiply(circle1.r))  # 通过圆心向量得到交点
        return [position]
    # 一般情况，通过边长求角度
    cos_value = (circle1.r**2+center_pos_dif**2-circle2.r**2)/(2*circle1.r*center_pos_dif)
    angle = math.acos(cos_value)/(2*math.pi)*360
    # 通过角度，转向得到两个交点的坐标
    r_dir = c1_to_c2_dir.to_unit_dir().multiply(circle1.r)
    return [circle1.center_pos.add(r_dir.rotate(angle)), circle1.center_pos.add(r_dir.rotate(-angle))]

圆与线段求交点

求圆与线段的交点可以转换为：

1.求圆与线段所在的直线的交点

2.判断线段所在的直线上的点是否在线段上

而求圆与线段所在的直线的交点可以转换为：

1.直线过圆心O的垂直线与直线的交点A

2.判断点A到圆心O的距离H，如果大于半径R直接返回。

3.通过直角3三角形一个变的长度H与斜边的长度R求出点A到目标交点的距离l

其中直线可以等价为很长的线段

代码与流程解析如下：

def get_intersection_points_by_line_segment_and_circle(line_segment:LineSegment,circle:Circle):
    line_dir = line_segment.get_dir()
    len_square = line_dir.len()
    if len_square == 0:
        return []
    line_dir = line_dir.to_unit_dir()
    max_size = 10000
    line = LineSegment(line_segment.start.add(line_dir.multiply(max_size)),
                       line_segment.start.reduce(line_dir.multiply(max_size)))
    circle_line = LineSegment(circle.center_pos.add(line_dir.rotate(90).multiply(max_size)),
                       circle.center_pos.reduce(line_dir.rotate(90).multiply(max_size)))
    points = get_intersection_points_by_line_segments(line,circle_line)  # 求直线过圆心O的垂直线与直线的交点
    if len(points) == 0:  # 预防一下
        return []
    point_a = points[0]
    h = point_a.reduce(circle.center_pos).len()
    if h > circle.r:  # 太远了
        return []

    dif_len = (circle.r**2 - h**2)**0.5
    intersection_points = []
    if dif_len == 0:  # 圆与线段所在的直线相切
        intersection_points = [point_a]
    else:  
        unit_dir = line_dir.to_unit_dir()
        intersection_points = [point_a.add(unit_dir.multiply(dif_len)), point_a.reduce(unit_dir.multiply(dif_len))]
    ret = []
    for position in intersection_points:  # 过滤不在线段上的点
        if line_segment.line_position_in_line_segment(position):
            ret.append(position)
    return ret

---

工具实际使用下来还是比较麻烦的：

1.没法直观的调整图形的位置。

2.也没有添加文本的功能。

有待后续完善。