一、简介
元学习的目标是在各种学习任务上训练模型,这样它就可以只使用少量的训练样本来解决新任务。
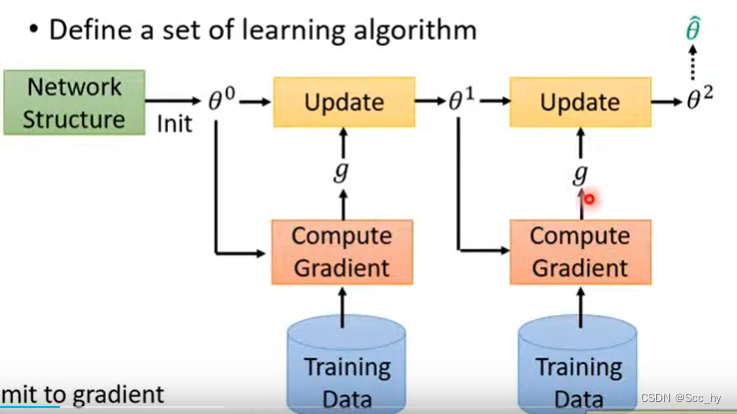
论文所提出的算法训练获取较优模型的参数,使其易于微调,从而实现快速自适应。该算法与任何用梯度下降训练的模型兼容,适用于各种学习问题,包括分类、回归和强化学习。
论文中表明,该算法在few-shot image classification基准上达到了SOTA的性能,在few-shot regression上也产出了良好的结果,并加速了策略梯度强化学习的微调。
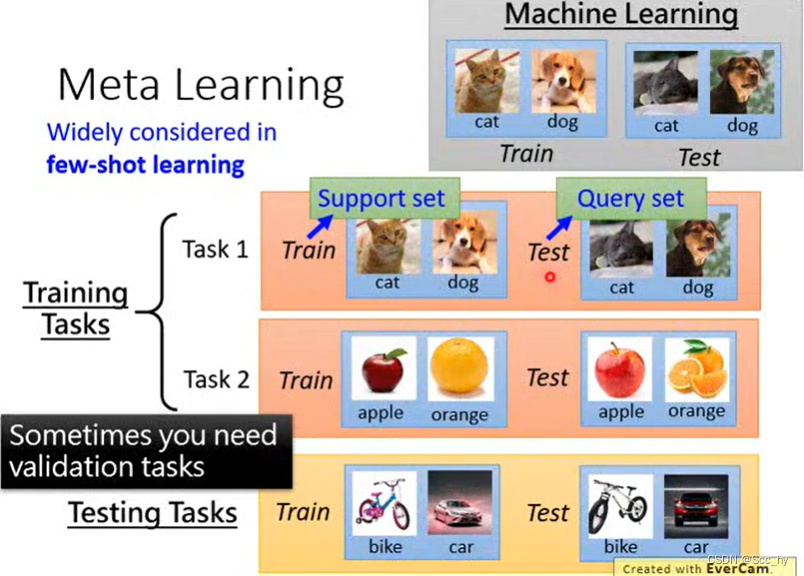
1.1 元学习与一般ML的区别
- ML: 根据给定数据找到一个
函数f,后续在相同的任务上运用该函数 - Meta Learning: 根据大量任务(数据)找一个
F可以输出f的能力,后续运用的时候在F上进行较少数据量的update后就可以得到对应运用任务的函数f
二、算法思路与伪代码(监督学习)
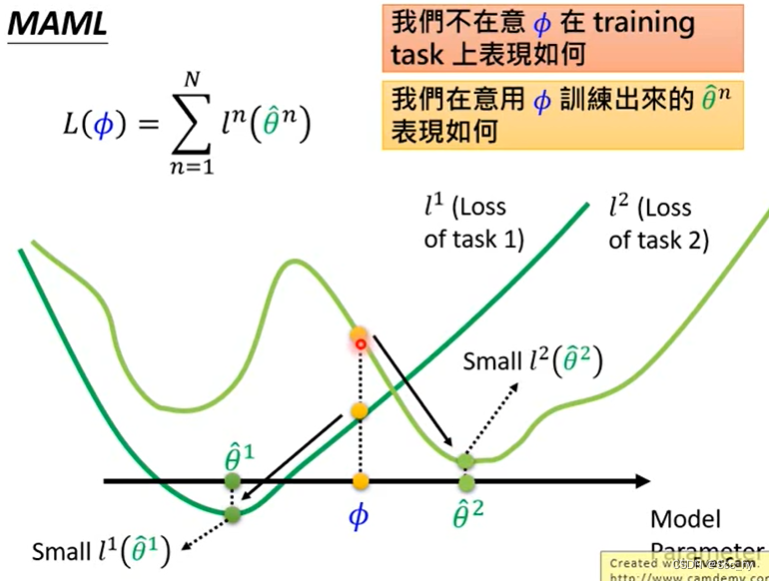
2.1 主要思路
核心思路就是找到一个较好的初始参数值,可以在任何同一类型的任务上进行少量数据较少次数update 后就可以得到较好的模型,下图展示了meta Learning 最终学习的参数
ϕ
\phi
ϕ
2.2 伪代码
Algorithm2 MAML for Few-Shot Supervised Learning Require: p ( T ) : distribution over tasks Require: α : 一系列task训练-supportSet,梯度更新学习率-在循环内更新 β : 一系列task评估-querySet,梯度更新学习率-在循环外更新 1: 初始化参数 θ 2: while not done do 3: 从任务集合中抽取任务 T i ∼ p ( T ) 4: for all T i do 5: 从任务中抽取k shot个样本 D = { X j , Y j } ∈ T i 6: 基于任务的损失函数计算损失 L T i = l ( Y j , f θ i ( X j ) ) 7: 基于损失函数计算梯度, 并更新参数 ∂ L T i ∂ θ i = ∇ θ L T i ( f θ ) θ i ′ = θ − α ∇ θ L T i ( f θ ) 8: 从任务中抽取 q query 个样本 D ′ = { X j , Y j } ∈ T i 基于更新后的 θ ′ 进行预测并计算损失,用于循环后更新 L T i ′ = l ( Y j , f θ i ′ ( X j ) ) 计算梯度 ∂ L T i ′ ∂ θ i ′ = ∇ θ L T i ′ ( f θ ′ ) 计算最终梯度 ∇ θ L T i ( f θ ′ ) = ∂ L T i ′ ∂ θ i = ∂ L T i ′ ∂ θ i ′ ∂ θ i ′ ∂ θ i 9: end for 10: Update θ ← θ − β ∑ T i ∼ p ( T ) ∇ θ L T i ( f θ ′ ) 11: end while r e t u r n θ \begin{aligned} &\rule{110mm}{0.4pt} \\ &\text{Algorithm2 MAML for Few-Shot Supervised Learning}\\ &\rule{110mm}{0.4pt} \\ &\textbf{Require: } p(\mathcal{T}): \text{distribution over tasks}\\ &\textbf{Require: } \alpha \text{: 一系列task训练-supportSet,梯度更新学习率-在循环内更新} \\ &\hspace{17mm} \beta \text{: 一系列task评估-querySet,梯度更新学习率-在循环外更新}\\ &\rule{110mm}{0.4pt} \\ &\text{ 1: 初始化参数 } \theta \\ &\text{ 2: }\textbf{while }\text{not done }\textbf{do }\\ &\text{ 3: }\hspace{5mm}\text{从任务集合中抽取任务 }\mathcal{T}_i \sim p(\mathcal{T}) \\ &\text{ 4: }\hspace{5mm}\textbf{for all }\mathcal{T}_i\textbf{ do }\\ &\text{ 5: }\hspace{10mm}\text{从任务中抽取k shot个样本} \mathcal{D}=\{X^j, Y^j\} \in \mathcal{T}_i\\ &\text{ 6: }\hspace{10mm}\text{基于任务的损失函数计算损失} \mathcal{L}_{\mathcal{T}_i}=l(Y^j, f_{\theta_{i}}(X^j))\\ &\text{ 7: }\hspace{10mm}\text{基于损失函数计算梯度, 并更新参数} \frac{\partial{\mathcal{L}_{\mathcal{T}_i}}}{\partial \theta_i} = \nabla_\theta \mathcal{L}_{\mathcal{T}_i}(f_\theta) \\ &\hspace{17mm} \theta_i^{\prime} = \theta - \alpha \nabla_\theta \mathcal{L}_{\mathcal{T}_i}(f_\theta) \\ &\text{ 8: }\hspace{10mm}\text{从任务中抽取 q query 个样本} \mathcal{D}^{\prime}=\{X^j, Y^j\} \in \mathcal{T}_i\\ &\hspace{15mm} \text{基于更新后的}\theta^{\prime}\text{进行预测并计算损失,用于循环后更新} \mathcal{L}^{\prime}_{\mathcal{T}_i}=l(Y^j, f_{\theta^{\prime}_{i}}(X^j))\\ &\hspace{15mm} \text{计算梯度}\frac{\partial{\mathcal{L}^{\prime}_{\mathcal{T}_i}}}{\partial \theta^{\prime}_i} = \nabla_\theta \mathcal{L}^{\prime}_{\mathcal{T}_i}(f_{\theta^{\prime}}) \\ &\hspace{15mm} \text{计算最终梯度} \nabla_\theta \mathcal{L}_{\mathcal{T}_i}(f_{\theta^{\prime}}) = \frac{\partial{\mathcal{L}^{\prime}_{\mathcal{T}_i}}}{\partial \theta_i}=\frac{\partial{\mathcal{L}^{\prime}_{\mathcal{T}_i}}}{\partial \theta^{\prime}_i}\frac{\partial \theta^{\prime}_i}{\partial \theta_i} \\ &\text{ 9: }\hspace{5mm}\textbf{end for} \\ &\text{10: }\hspace{5mm}\text{Update } \theta \leftarrow \theta - \beta \sum_{\mathcal{T}_i \sim p(\mathcal{T})} \nabla_\theta \mathcal{L}_{\mathcal{T}_i}(f_{\theta^{\prime}}) \\ &\text{11: }\textbf{end while } \\ &\bf{return} \: \theta \\[-1.ex] &\rule{110mm}{0.4pt} \\[-1.ex] \end{aligned} Algorithm2 MAML for Few-Shot Supervised LearningRequire: p(T):distribution over tasksRequire: α: 一系列task训练-supportSet,梯度更新学习率-在循环内更新β: 一系列task评估-querySet,梯度更新学习率-在循环外更新 1: 初始化参数 θ 2: while not done do 3: 从任务集合中抽取任务 Ti∼p(T) 4: for all Ti do 5: 从任务中抽取k shot个样本D={Xj,Yj}∈Ti 6: 基于任务的损失函数计算损失LTi=l(Yj,fθi(Xj)) 7: 基于损失函数计算梯度, 并更新参数∂θi∂LTi=∇θLTi(fθ)θi′=θ−α∇θLTi(fθ) 8: 从任务中抽取 q query 个样本D′={Xj,Yj}∈Ti基于更新后的θ′进行预测并计算损失,用于循环后更新LTi′=l(Yj,fθi′(Xj))计算梯度∂θi′∂LTi′=∇θLTi′(fθ′)计算最终梯度∇θLTi(fθ′)=∂θi∂LTi′=∂θi′∂LTi′∂θi∂θi′ 9: end for10: Update θ←θ−βTi∼p(T)∑∇θLTi(fθ′)11: end while returnθ
三、简单实践
用Meta Learning 学习
y
=
a
×
s
i
n
(
x
+
b
)
y = a\times sin(x + b)
y=a×sin(x+b), 不同的a, b代表不同的任务
3.1 任务数据准备
class SineWaveTask:
def __init__(self):
self.a = np.random.uniform(0.1, 5.0)
self.b = np.random.uniform(1, 2 * np.pi)
self.train_x = None
def f(self, x):
return self.a * np.sin(x + self.b)
def train_set(self, size=10, force_new=False):
if self.train_x is None and not force_new:
self.train_x = np.random.uniform(-5, 5, size)
x = self.train_x
elif not force_new:
x = self.train_x
else:
x = np.random.uniform(-5, 5, size)
y = self.f(x)
return torch.Tensor(x).float(), torch.Tensor(y).float()
def test_set(self, size=50):
x = np.linspace(-5, 5, size)
y = self.f(x)
return torch.Tensor(x).float(), torch.Tensor(y).float()
def plot(self, *args, **kwargs):
x, y = self.test_set()
return plt.plot(x.cpu().detach().numpy(), y.cpu().detach().numpy(), *args, **kwargs)
SineWaveTask().plot()
SineWaveTask().plot()
SineWaveTask().plot()
plt.show()
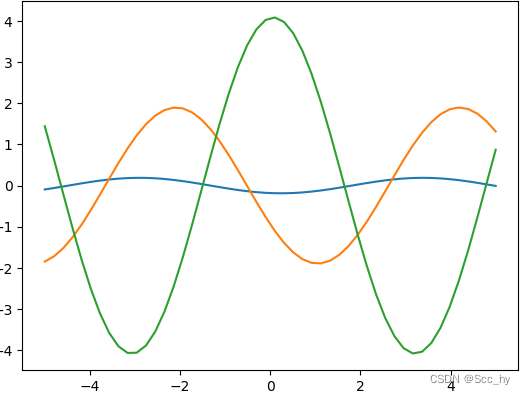
3.2 模型
因为query task中需要用support task后的参数进行推理,后进行二阶导来update 参数,所以多了一个query_forward 方法
class sineModel(nn.Module):
def __init__(self):
super(sineModel, self).__init__()
self.l1 = nn.Linear(1, 40)
self.l2 = nn.Linear(40, 40)
self.head = nn.Linear(40, 1)
def forward(self, x):
x = torch.relu(self.l1(x))
x = torch.relu(self.l2(x))
return self.head(x)
def query_forward(self, x, support_param_dict):
x = torch.relu(
F.linear(x, support_param_dict['l1.weight'], support_param_dict['l1.bias'])
)
x = torch.relu(
F.linear(x, support_param_dict['l2.weight'], support_param_dict['l2.bias'])
)
return F.linear(x, support_param_dict['head.weight'], support_param_dict['head.bias'])
SUPPORT_QUERY_TASKS = [SineWaveTask() for _ in range(1000)]
TEST_TASKS = [SineWaveTask() for _ in range(1000)]
3.3 MAML
def maml_sine(model, epochs, lr=1e-3, inner_lr=0.1, batch_size=1, first_order=False):
opt = torch.optim.Adam(model.parameters(), lr=lr)
loss_fn = nn.MSELoss()
ep_loss = []
for ep_i in range(epochs):
tqd_bar = tqdm(
enumerate(random.sample(SUPPORT_QUERY_TASKS, len(SUPPORT_QUERY_TASKS))),
total=len(SUPPORT_QUERY_TASKS)
)
tqd_bar.set_description(f'[ {ep_i+1:02d} / {epochs:02d} ]')
task_loss = []
for idx, suport_t in tqd_bar:
fast_weights = OrderedDict(model.named_parameters())
s_x, s_y = suport_t.train_set(force_new=False)
q_x, q_y = suport_t.train_set(force_new=True)
# support
for _ in range(1):
s_y_hat = model(torch.Tensor(s_x[:, None]))
loss = loss_fn(s_y_hat, torch.Tensor(s_y.reshape(-1, 1)))
grads = torch.autograd.grad(loss, fast_weights.values(), create_graph=not first_order) # 便于进行二阶导
fast_weights = OrderedDict(
(name, param - inner_lr * (grad.detach().data if first_order else grad) )
for ((name, param), grad) in zip(fast_weights.items(), grads)
)
# query
logits = model.query_forward(torch.Tensor(q_x[:, None]), fast_weights)
loss = loss_fn(logits, torch.Tensor(q_y.reshape(-1, 1)))
task_loss.append(loss)
if (idx + 1) % batch_size == 0:
# update
model.train()
opt.zero_grad()
meta_batch_loss = torch.stack(task_loss).mean()
meta_batch_loss.backward()
opt.step()
loss_item = meta_batch_loss.cpu().detach().numpy()
tqd_bar.set_postfix({'loss': "{:.3f}".format(loss_item)})
task_loss = []
ep_loss.append(loss_item)
return ep_loss
sine_model = sineModel()
ep_losses = maml_sine(sine_model, epochs=5, lr=1e-3, inner_lr=0.02, batch_size=2, first_order=False)
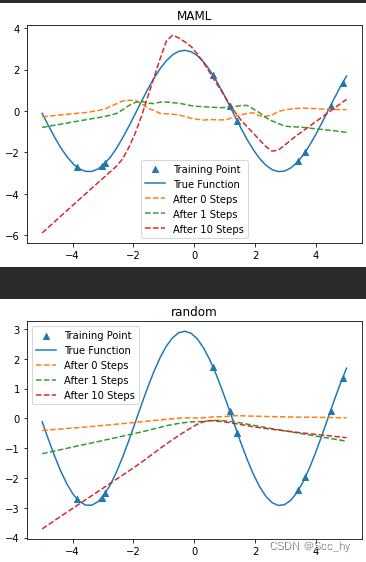
结果查看
全部代码见笔者github:maml.ipynb
maml训练结果显然要好于随机模型
参考
- Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks
- 李宏毅老师的课程PPT(国立台湾大学)