微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

1、平稳随机过程的定义
(1)严平稳随机过程(狭义平稳随机过程)定义
若一个随机过程ξ(t)的统计特性与时间起点无关,即时间平移不影响其任何统计特性,则该随机过程为严格意义下的平稳随机过程
对于任意正整数n和所有实数都满足以下公式:
fn(x1,x2……,xn;t1,t2……,tn)=fn(x1,x2……,xn;t1+△,t2+△……,tn+△)
一维概率密度函数与时间t无关,f1(x1,t1)=f1(x1)
二维分布函数只与时间间隔τ=t2-t1有关,f2(x1,x2;t1,t2)=f2(x1,x2;τ)
(2)广义平稳随机过程
两个广义平稳随机过程的满足条件
①均值与t无关,为常数a;
②自相关函数只与时间间隔τ=t2-t1有关,即R(t1,t1+τ)=R(τ)
(3)严平稳随机过程一定是广义平稳随机过程,反之则不一定成立。
(4)在通信系统中所遇到的信号及噪声,大多数可视为平稳的随机过程,以广义平稳随机过程研究。
2、各态经历性(遍历性)
(1)平稳过程的统计平均值等于任一次实现的时间平均值,则称为该平稳过程具有各态经历性
时间均值和时间相关函数

(2)随机过程中的任一次实现都经历了随机过程的所有可能状态,可用一次实现的“时间平均”值代替过程的“统计平均”值,从而简化测量和计算的问题。
(3)具有各态经历的随机过程一定是平稳过程,反之则不一定成立。
(4)在通信系统中所遇到的随机信号及噪声,一般均能满足各态经历条件。
3、平稳过程的自相关函数
平稳过程ξ(t)的自相关函数为R(τ)=E[ξ(t)ξ(t+τ)]
主要性质有:
①R(0)=E[(ξ(t))^2],表示ξ(t)的平均功率;
②R(τ)=R(-τ),表示τ的偶函数;
③|R(τ)|≤R(0),表示R(τ)的上界;
④R(∞)=(E[ξ(t)])2=a2,表示ξ(t)的直流功率
⑤R(0)-R(∞)=σ2,σ2是方差,是平稳过程ξ(t)的交流功率。
4、平稳过程的功率谱密度
(1)随机过程的频谱特性使用它的功率谱密度来表述。
对于任意的确定功率信号f(t),功率谱密度p(f)计算为:

其中FT(f)是f(t)的截断函数fT(t)对应的频谱函数
对所有的样本的功率谱的统计平均计算,过程的功率谱密度为:

(2)维纳—辛钦定理
联系频域和时域两种分析方法的基本关系式
平稳过程的功率谱密度Pξ(f)与其自相关函数R(τ)是一对傅里叶变换关系,即R(τ)<=>Pξ(f)

主要性质有:
(1)当τ=0时,可得平稳过程的平均功率,此为频域分析方法下的计算公式

而R(0)=E[(ξ(t))^2],表示ξ(t)的平均功率,此为时域分析方法下的计算公式
(2)各态经历过程的任一样本函数的功率谱密度等于过程的功率谱密度;
(3)功率谱密度Pξ(f)具有非负性和实偶性,即Pξ(f)≥0,Pξ(-f)=Pξ(f)
通信原理板块——平稳随机过程
news2026/2/21 17:47:08
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/967013.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
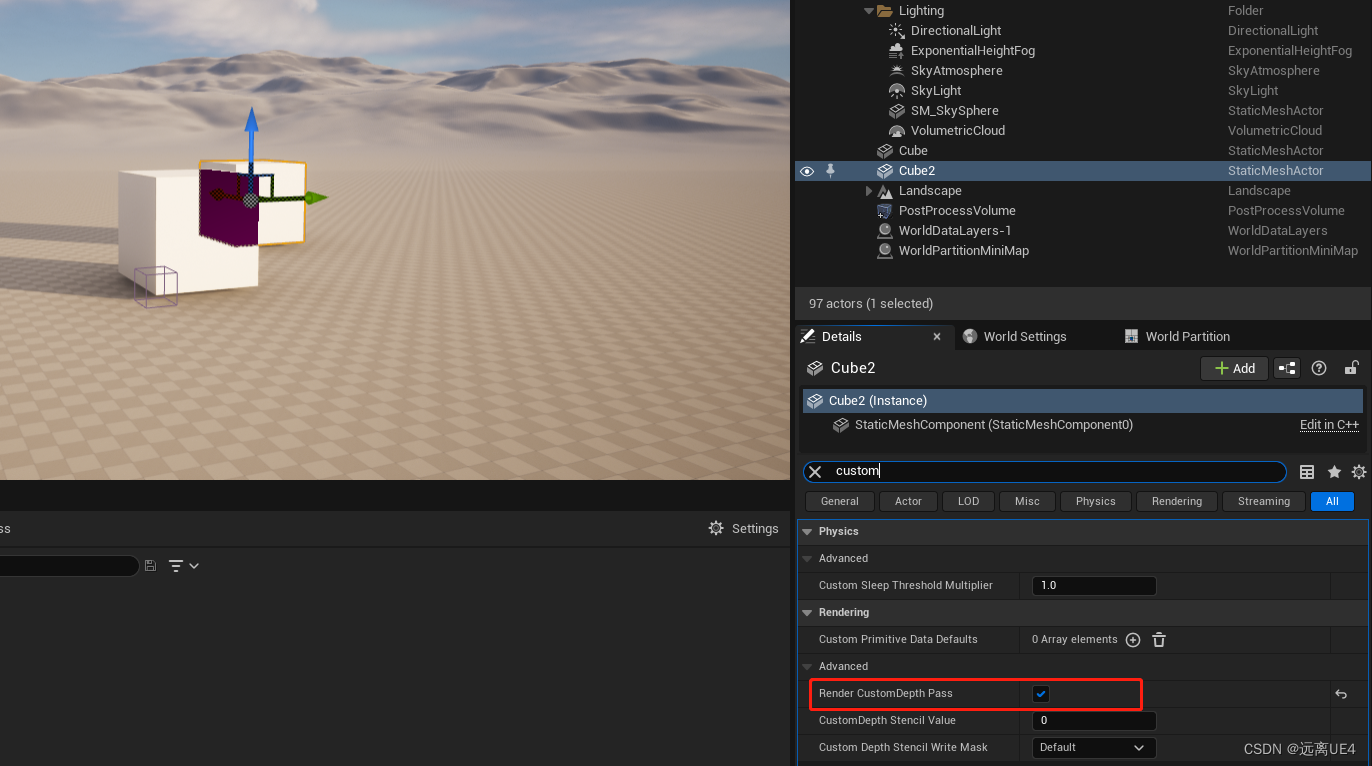
UE4 显示遮挡物体
SceneDepth是你相机能够看见的物体的深度距离
CustomDepth是你相机包括看不见被遮挡的物体的深度距离
如果CustemDepth比SceneDepth的距离相等,那么就是没有被遮挡的物体,如果被遮挡那么就是CustemDepth比SceneDepth深度距离远,然后再做对应…
PYTHON知识点学习-循环语句
🚀write in front🚀 🔎大家好,我是Aileen★。希望你看完之后,能对你有所帮助,不足请指正!共同学习交流🔎 🆔本文由 Aileen_0v0★ 原创 CSDN首发🐒 如需转载还…
【机器学习】线性回归
Model Representation 1、问题描述2、表示说明3、数据绘图4、模型函数5、预测总结附录 1、问题描述
一套 1000 平方英尺 (sqft) 的房屋售价为300,000美元,一套 2000 平方英尺的房屋售价为500,000美元。这两点将构成我们的数据或训练集。面积单位为 1000 平方英尺&a…
Swift 如何从图片数据(Data)检测原图片类型?
功能需求
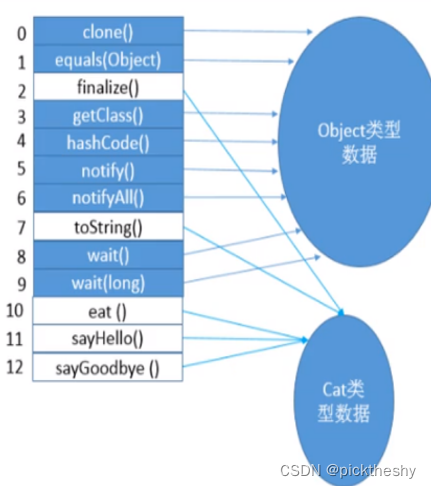
如果我们之前把图片对应的数据(Data)保持在内存或数据库中,那么怎么从 Data 对象检测出原来图片的类型呢? 如上图所示:我们将 11 张不同类型的图片转换为 Data 数据,然后从 Data 对象正确检测出了原图片类型。
目前,我们的代码可以检测出 jpeg(jpg), tiff,…
WebRTC 安全之一
WebRTC 的安全需要满足三个基本需求 Authentication 用户访问需要认证Authorization 用户访问需要授权Audit 用户的访问应该可被追踪和审查 其中前两项也可以归结为 CIA Confidentiality 机密性:信息需要保密, 访问权限也需要控制Integrity 完整性&#…
Spring Cloud集成Nacos配置中心/注册中心
Spring Cloud版本
2021.0.5
Spring Cloud Alibaba版本
2021.0.5.0
Spring Boot版本
2.7.10
pom文件
需要放在依赖管理的pom文件
<dependencyManagement><dependencies><!-- spring boot依赖 --><dependency><groupId>org.springframewor…
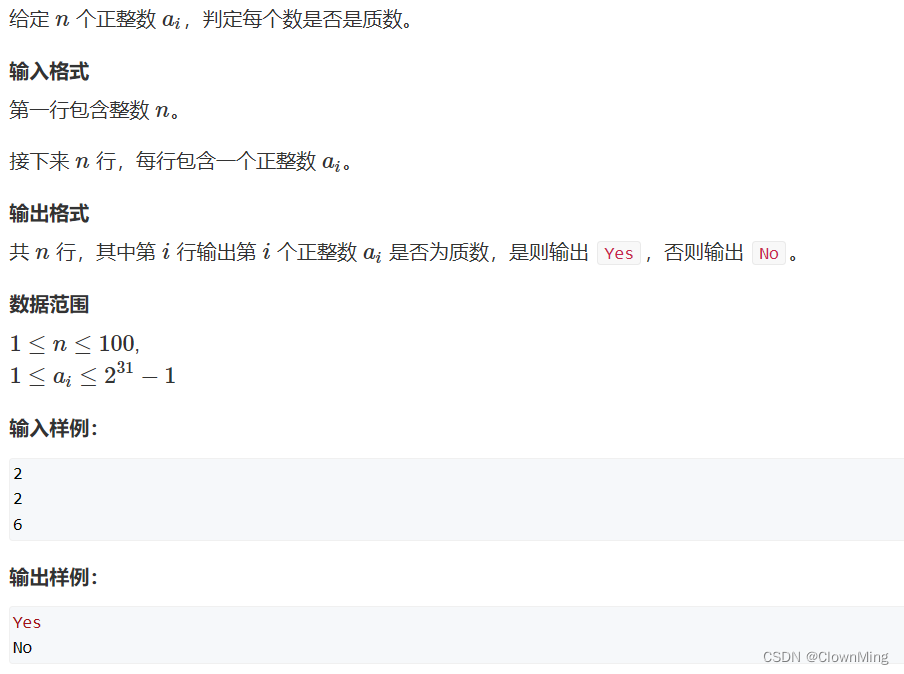
2023-9-3 试除法判定质数
题目链接:试除法判定质数 #include <iostream>using namespace std;bool is_prime(int n)
{if(n < 2) return false;for(int i 2; i < n / i; i){if(n % i 0) return false;}return true;
}int main()
{int n;cin >> n;while(n--){int x;cin &g…
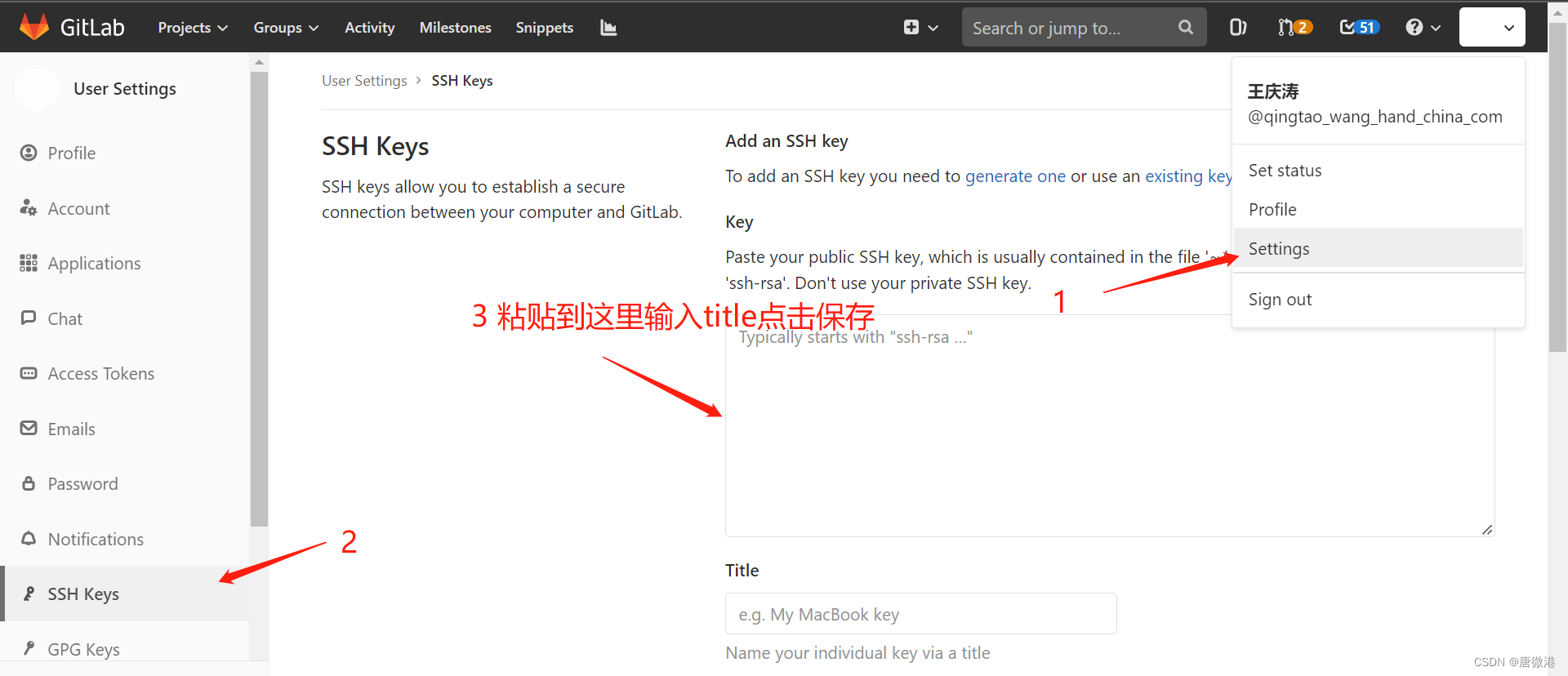
git大文件推送报错
报错信息
不多掰扯,直接上报错信息和截图
Delta compression using up to 8 threadsRPC failde; HTTP 413 curl 22 The requested URL returned error: 413 Request Entity Too Large从以上的报错信息不难看出推送仓库的时候,请求体过大,为…
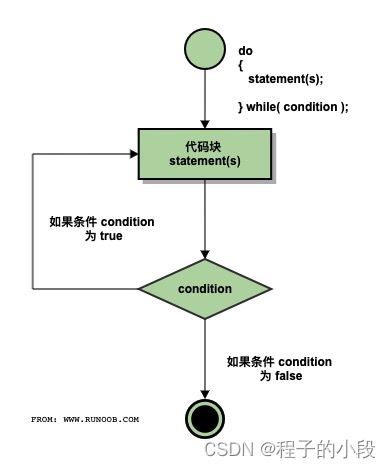
C++ do...while 循环
不像 for 和 while 循环,它们是在循环头部测试循环条件。do…while 循环是在循环的尾部检查它的条件。
do…while 循环与 while 循环类似,但是 do…while 循环会确保至少执行一次循环。
语法
C 中 do…while 循环的语法:
do
{statement(s…
AD16 基础应用技巧(一些 “偏好“ 设置)
1. 修改铺铜后自动更新铺铜
AD16 铺铜 复制 自动变形 偏好设置
将【DXP】中的【参数选择】。
将【PCB Editor】中的【General】,然后勾选上【Repour Polygons After Modification】。
2. PCB直角走线处理与T型滴泪
一些没用的AD技巧——AD PCB直角走线处理与…
iOS练手项目知识点汇总
基础理解篇
Objective-C是一种面向对象的编程语言,它支持元编程。元编程是指编写程序来生成或操纵其他程序的技术。 Objective-C中,元编程可以使用Objective-C的动态特性来实现。例如可以使用Objective-C的运行时函数来动态地创建类、添加属性和方法等等…
给视频添加背景图片,让它们更具魅力!
想要让你的视频更加出彩吗?给它们添加背景图片是不错的选择!但是,如何做到呢?不用担心,我们的视频剪辑高手可以帮助你轻松实现!我们提供多种背景图片选择,你可以根据自己的喜好和需求进行选择。…
程序员自由创业周记#7:仲裁
没想到
没想到写的周记会有这么多人看,还能收到这么多陌生(或熟悉)朋友的真诚建议、鼓励、甚至是打赏,几乎所有的评论和私信我都认真的回复了,本想的是通过网友和朋友的监督坚定我创业的信念,有点外界压力也能迫使自己持续输出一…
P1886 滑动窗口 /【模板】(双端队列)+双端队列用法
例题
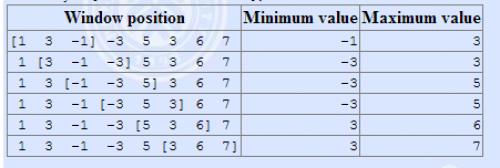
有一个长为 n 的序列 a,以及一个大小为 k 的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如:
The array is [1,3,−1,−3,5,3,6,7],and k3。 输入格式
输入一共有两行…
WideDeep模型介绍
文章目录 1. Wide&Deep模型的记忆能力和泛化能力2. Wide&Deep模型的结构3. Wide&Deep模型的进化——Deep&Cross模型4. Wide&Deep模型的影响力 Wide&Deep模型是
记忆能力和
泛化能力的综合,是谷歌在2016年提出的。正如其名,Wid…
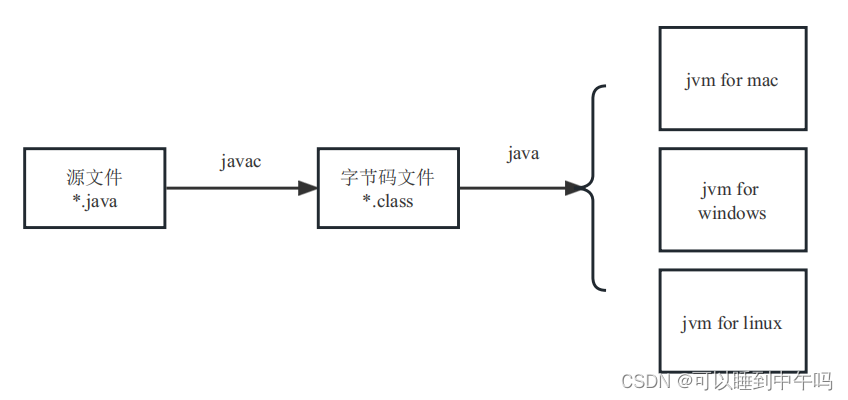
java运行程序流程
java运行程序流程
检查JDK环境 java -version
新建Java文件(源文件)Hello.java 打开记事本,输入 public class Hello {public static void main(String[] args) {System.out.println("Hello");}
} 保存文件,把文件后缀…
C++极简内存泄露检测工具(34行代码实现)
工具特点
1 极度简单:34行代码实现,线程安全
2 入寝式检测:需要给现有重点怀疑的类添加一行入寝代码
3 只针对类类型:动态数组需要使用更为复杂的技术,不在检测能力范围之内。考虑到大部分C代码都以类实现代码&…
Python零基础超详细教程:字典(Dictionary)相关介绍使用
前言
嗨喽~大家好呀,这里是魔王呐 ❤ ~! Python字典是另一种可变容器模型,
且可存储任意类型对象,如字符串、数字、元组等其他容器模型。
python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取
一、创建字典
字典由键和对应值…