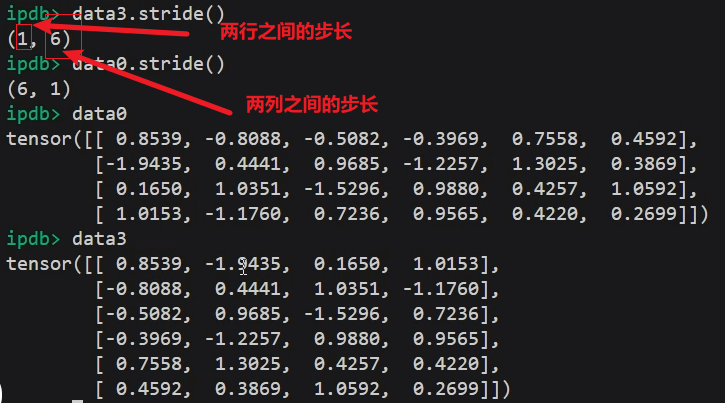
微分
函数的微分是指对函数的局部变化的一种线性描述。微分可以近似地描述当函数自变量的取值作足够小的改变时,函数的值是怎样改变的。。对于函数
y
=
f
(
x
)
y = f(x)
y=f(x) 的微分记作:
d
y
=
f
′
(
x
)
d
x
d_y = f^{'}(x)d_x
dy=f′(x)dx
微分和导数的区别在于:导数是曲线在那个点的切线斜率,而微分是那个切线的一元线性方程。
微分的几何意义:是用局部切线段近似代替曲线段,即非线性函数局部线性化。
积分
积分可以分为定积分和不定积分两种。
定积分
对于函数
f
(
x
)
f(x)
f(x) 在区间 [a,b] 上定积分记作:
∫
b
a
f
(
x
)
d
x
\int^{a}_{b}f(x)d_x
∫baf(x)dx
其几何意义为函数
f
(
x
)
f(x)
f(x)在区间[a,b]上的覆盖面积,如下图:


不定积分
不定积分是导数的逆运算,即反导数。当
f
f
f是
F
F
F的导数时,则
F
F
F是
f
f
f的不定积分。常用公式如下:
- ∫ a d x = a x + C \int ad_x = ax + C ∫adx=ax+C
- ∫ x a d x = 1 a + 1 x a + 1 + C \int x^{a}d_x = {1\over a+1}x^{a+1} + C ∫xadx=a+11xa+1+C
- ∫ 1 x = l n ∣ x ∣ + C \int {1 \over x} = ln|x| + C ∫x1=ln∣x∣+C
- ∫ a x d x = a x l n a + C \int {a^xdx} = {a^x\over lna} + C ∫axdx=lnaax+C
- ∫ s i n x d x = − c o s x + C \int sin\ x\ dx = -cos\ x + C ∫sin x dx=−cos x+C
- ∫ c o s x d x = s i n x + C \int cos\ x\ dx = sin\ x + C ∫cos x dx=sin x+C
- ∫ t a n x d x = − l n ∣ c o s x ∣ + C \int tan\ x\ dx = -ln|cos\ x| + C ∫tan x dx=−ln∣cos x∣+C
泰勒公式
用多项式拟合原函数:
f
(
x
)
=
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
+
f
′
′
(
x
0
)
2
!
(
x
−
x
0
)
2
+
.
.
.
+
f
n
(
x
0
)
n
!
(
x
−
x
0
)
n
+
.
.
.
f(x) = f(x_0) + f^{'}(x_0)(x - x_0) + {f^{''}(x_0) \over 2!}(x - x_0)^2 + ... + {f^{n}(x_0) \over n!}(x - x_0)^n + ...
f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+...+n!fn(x0)(x−x0)n+...
几何分析
如下内容来自如何通俗地解释泰勒公式?,因为在
x
0
x_0
x0点的任意阶导数都为常数,暂且不管,对于幂函数有如下特点:
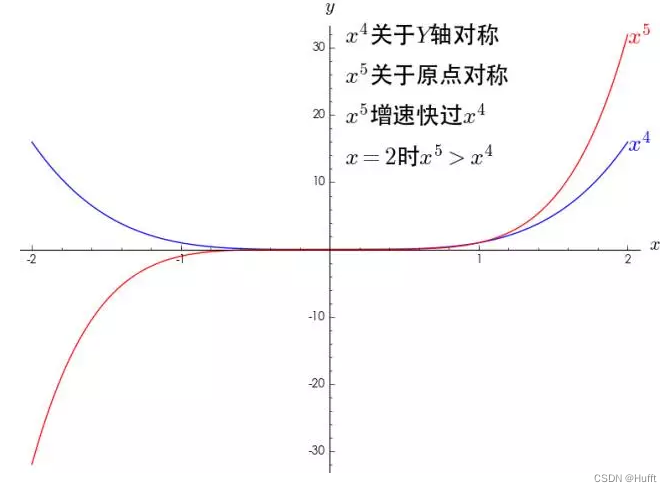
多个幂函数相加:

增加阶乘后效果如下:

通过改变系数,多项式可以像铁丝一样弯成任意的函数曲线,对于
e
(
x
)
e(x)
e(x)拟合: