目录
什么是最小二乘法
残差是什么意思
线性模型
线性回归
方法一:解析解法
代码实战:
方法二:数值解法
代码实战:
解析法(最小二乘)还是数值法(梯度下降),如何选择?
什么是最小二乘法
最小二乘法公式是一个数学的公式,在数学上称为曲线拟合,此处所讲最小二乘法,专指线性回归方程。

最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
扩展资料:
普通最小二乘估计量具有上述三特性:
1、线性特性
所谓线性特性,是指估计量分别是样本观测值的线性函数,亦即估计量和观测值的线性组合。
2、无偏性
无偏性,是指参数估计量的期望值分别等于总体真实参数。
3、最小方差性
所谓最小方差性,是指估计量与用其它方法求得的估计量比较,其方差最小,即最佳。最小方差性又称有效性。这一性质就是著名的高斯一马尔可夫( Gauss-Markov)定理。这个定理阐明了普通最小二乘估计量与用其它方法求得的任何线性无偏估计量相比,它是最佳的。
线性最小二乘法主要包括如下三种类型:
- 普通最小二乘法(Ordinary Least Squares, OLS)
- 加权最小二乘法(Weighted Least Squares, WLS)
- 广义最小二乘法(Generalized Least Squares, GLS )
残差是什么意思
- 残差=观测值-预测值
- 偏差=观测值-平均值

残差在数理统计中是指实际观察值与估计值(拟合值)之间的差。“残差”蕴含了有关模型基本假设的重要信息。如果回归模型正确的话, 我们可以将残差看作误差的观测值。
很多人在开始学习机器学习的时候都看不上线性回归,觉得这种算法太老太笨,不够fancy,草草学一下就去看随机森林、GBDT、SVM甚至神经网络这些模型去了。但是后来才发现线性回归依然是工业界使用最广泛的模型。而且线性回归细节特别多,技术面时被问到的概率也很大,希望大家能学好线性回归这块机器学习,也可能是一个offer的敲门砖。
学习中,顺着线性回归,可以引申出多项式回归、岭回归、lasso回归,此外还串联了逻辑回归、softmax回归、感知机。通过线性回归,还能巩固和实践机器学习基础,比如损失函数、评价指标、过拟合、正则化等概念。最后,线性回归与后续要学到的神经网络、贝叶斯、SVM、PCA等算法都有一定的关系。
本文将会出现不少数学公式,需要用到线性代数和微积分的一些基本概念。要理解这些方程式,你需要知道什么是向量和矩阵,如何转置向量和矩阵,什么是点积、逆矩阵、偏导数。
线性模型
线性模型的表达式很简单:


线性模型形式简单、易于建模,但却蕴涵着机器学习中一些重要的基本思想。许多功能更为强大的非线性模型(nonlinear model)可在线性模型的基础上通过引入层级结构或高维映射而得。此外,由于直观表达了各个特征在预测中的重要性,因此线性模型有很好的可解释性(comprehensibility)。
为什么需要 (Bias Parameter)? 类似于线性函数中的截距,在线性模型中补偿了目标值的平均值(在训练集上的)与基函数值加权平均值之间的差距。即打靶打歪了,但是允许通过平移固定向量的方式移动到目标点上(每个预测点和目标点之间的偏置都必须是固定的)。
其实,线性是描述自变量之间只存在线性关系,即自变量只能通过相加或者相减进行组合,通俗来说就行没有 这样的高次形式。
这样的高次形式。
线性回归


MSE物理意义怎么解释?
均方误差有非常好的几何意义,它对应了常用的欧几里得距离或简称“欧氏距离”(Euclidean distance)。基于均方误差最小化来进行模型求解的方法称为“最小二乘法”(least square method)。在线性回归中,最小二乘法就是试图找到一条直线,使所有样本到直线上的欧氏距离之和最小。

最小二乘法:使得所选择的回归模型应该使所有观察值的残差平方和达到最小
如何求解模型参数和呢?
- 一种是解析法,也就是最小二乘。
- 另一个是逼近法,也就是梯度下降。
方法一:解析解法
线性回归模型的最小二乘“参数估计”(parameter estimation)就是求解和,使得最小化的过程。
是关于和的凸函数(意思是可以找到全局最优解)。这里我们试图让均方误差MSE最小。
和表示和的解,是样本个数。这里的arg 是指后面的表达式值最小时的取值。
那么上面的公式我们如何求得参数呢? 这里我们又需要一些微积分(calculus)的知识,可以将分别对w和b求导,得到:
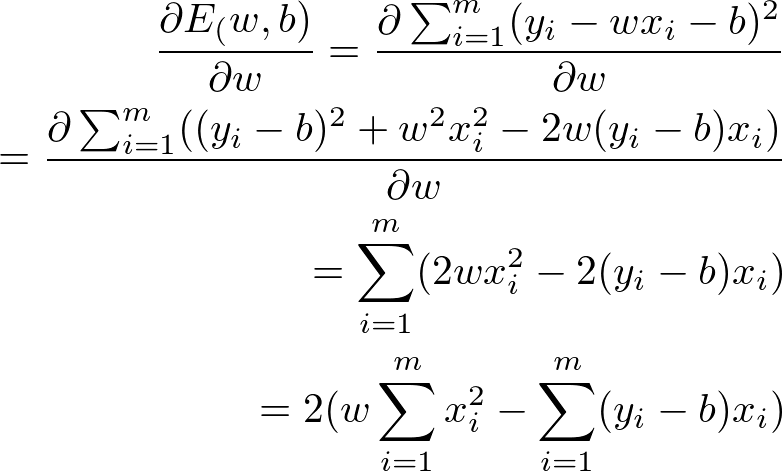
E对w求导
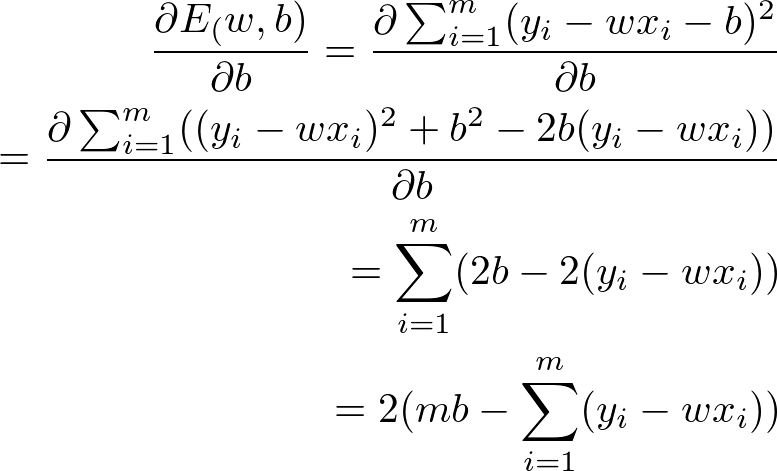
E对b求导

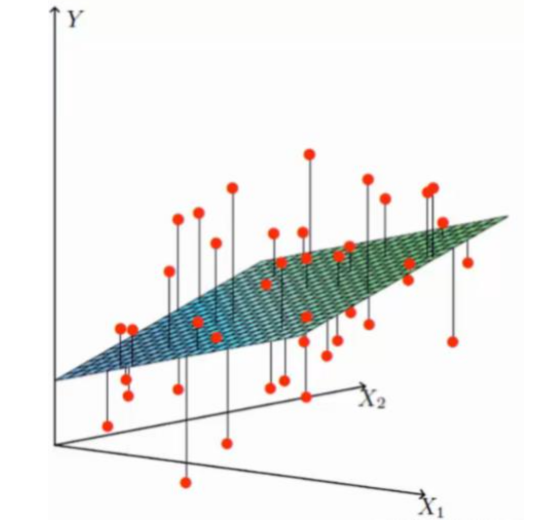
对于多个属性的讨论,通常这时就引入了矩阵表示,模型试图学得,使得。这就是“多元线性回归”(multivariate linear regression)。
将表示为的一个参数,那么:
然后对求导就可以得到矩阵的解(忽略了很多推导过程):
这里求解析解存在的问题是 在现实任务中往往不是满秩矩阵,所以无法求解矩阵的逆,故无法求得唯一的解。
-
非满秩矩阵:例如3个变量,但是只有2个方程,故无法求得唯一的解。
-
矩阵的逆:类似于数字的倒数(5对应1/5)目的是实现矩阵的除法。
解决方法:引入正则化(regularization)将矩阵补成满秩(这个坑,下一篇文章来填)
代码实战:
我们先生成一些数据,用于后面的实验。生成数据的函数是高斯噪声。
# 随机生成一些用于实验的线性数据
import numpy as np
np.random.seed(42)
m = 100 # number of instances
X = 2 * np.random.rand(m, 1) # column vector
y = 4 + 3 * X + np.random.randn(m, 1) # column vector
画个图来看看生成的数据。
import matplotlib.pyplot as plt
plt.figure(figsize=(6, 4))
plt.plot(X, y, "b.")
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.axis([0, 2, 0, 15])
plt.grid()
plt.show()
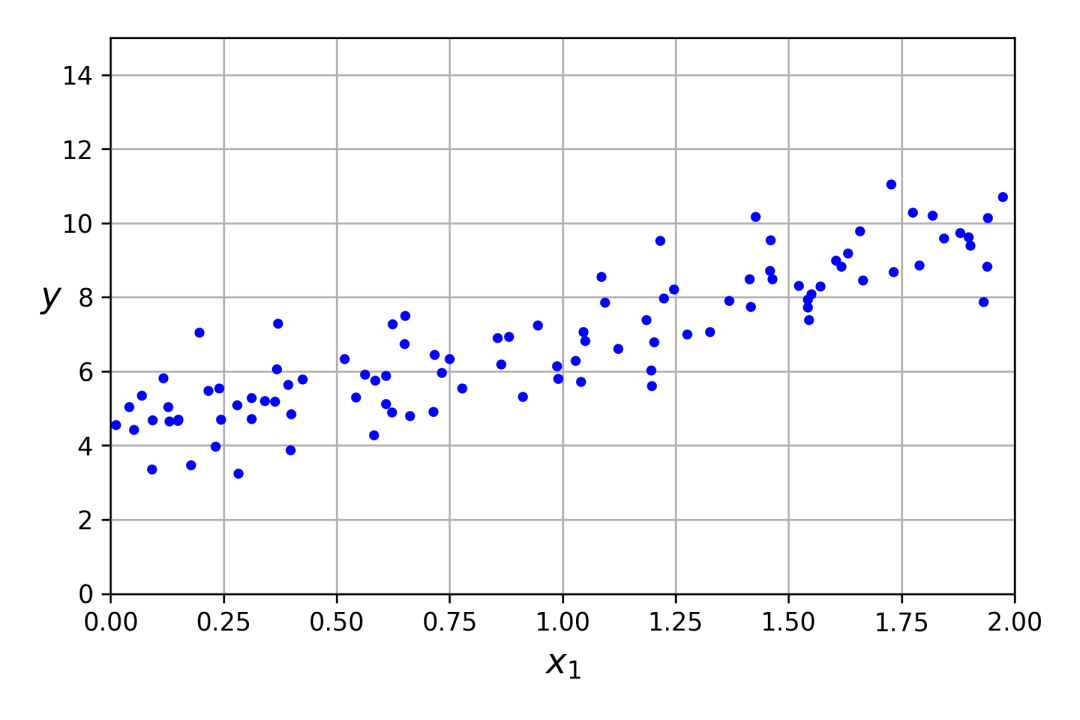
开始求解,也就是套公式。
# add x0 = 1 to each instance
X_b = np.c_[np.ones((100, 1)), X]
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
公式的结果theta_best的解为array([[4.21509616],[2.77011339]])。我们期待的是,得到的是,。非常接近,噪声的存在使其不可能完全还原为原本的函数。
现在可以用来做出预测了。预测结果为array([[4.21509616], [9.75532293]])。
X_new = np.array([[0], [2]])
# add x0 = 1 to each instance
X_new_b = np.c_[np.ones((2, 1)), X_new]
y_predict = X_new_b.dot(theta_best)
绘制模型的预测结果。
plt.plot(X_new, y_predict, "r-")
plt.plot(X, y, "b.")
plt.axis([0, 2, 0, 15])
plt.show()
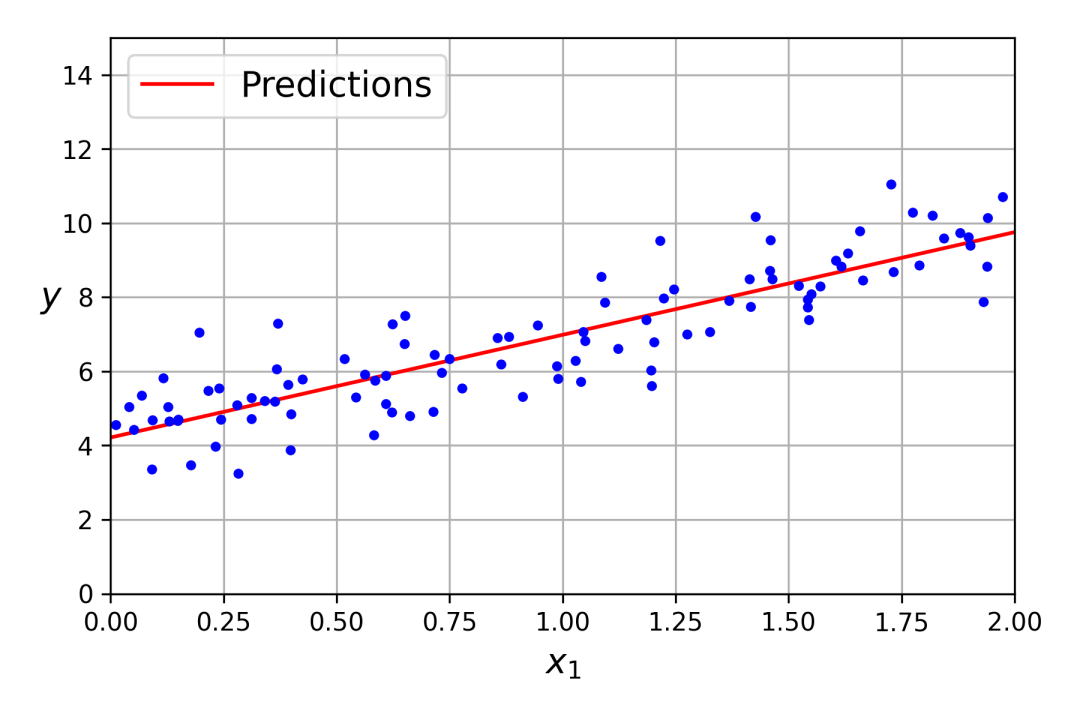
另外也可以直接调用最小二乘函数scipy.linalg.lstsq()进行计算:
theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y, rcond=1e-6)
theta_best_svd的计算结果为array([[4.21509616],[2.77011339]])。
方法二:数值解法
梯度下降,随机初始化和,通过逼近(沿着梯度下降的方向)的方式来求解(找到一个收敛的参数值)。
损失函数回顾:
公式里的和解析解部分的是一样的(只是换了下字母)。
注意到其中的参数,这个参数是可以简化部分求导(消掉)。除了参数外,其它部分与解析解部分是完全相同的。
梯度下降参数优化方法:
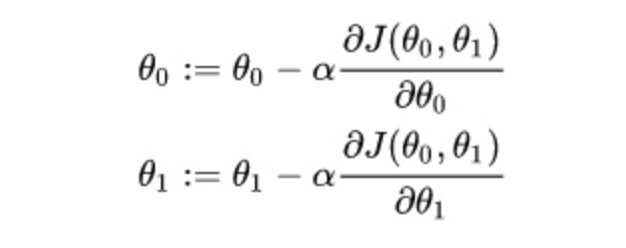
其中是学习率(learning rate)(学习率也经常用字母表示),是用来控制下降每步的距离(太小收敛会很慢,太大则可能跳过最优点),可以按照对数的方法来选择,例如0.1, 0.03, 0.01, 0.003, …….
梯度下降形象解释:把损失函数想象成一个山坡,目标是找到山坡最低的点。则随便选一个起点,计算损失函数对于参数矩阵在该点的偏导数,每次往偏导数的反向向走一步,步长通过来控制,直到走到最低点,即导数趋近于0的点为止。
梯度下降的过程可以通过程序来完成,动手练习,可以加深对于梯度下降方法的理解。
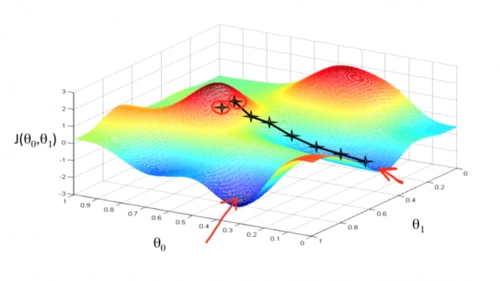
梯度下降有什么缺点?
-
最小点的时候收敛速度变慢,并且对初始点的选择极为敏感。
-
梯度下降有时会陷入局部最优解的问题中,即下山的路上有好多小坑,运气不好掉进坑里,但是由于底部梯度(导数)也为0,故以为找到了山的最底部。
-
步长选择的过大或者过小,都会影响模型的计算精度及计算效率。
解决方法:随机梯度下降、批量梯度下降、动量梯度下降
代码实战:
eta = 0.1 # learning rate
n_iterations = 1000
m = 100
theta = np.random.randn(2,1) # random initialization
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
计算的theta结果为array([[4.21509616],[2.77011339]]),是不是很简单?还可以更简单!
使用Scikit-Learn自带的随机梯度下降SGDRegressor类,该类默认优化平方误差成本函数。以下代码最多可运行1000个轮次,或者直到一个轮次期间损失下降小于0.001为止(max_iter=1000,tol=1e-3)。它使用默认eta0=0.1。
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1)
sgd_reg.fit(X, y.ravel())
解析法(最小二乘)还是数值法(梯度下降),如何选择?
1.本质相同:两种方法都是在给定已知数据(自变量 & 因变量)的前提下对因变量算出一个一般性的估值函数。然后对给定新数据进行估算。
2.目标相同:都是在已知数据的框架内,使得估算值与实际值的总平方差尽量更小(事实上未必一定要使用平方)。

4. 梯度下降法:一种数值方法(也可以叫优化方法),需要多次迭代来收敛到全局最小值。
-
需要给定
-
需要很多次迭代
-
在features很多的情况下运行良好(比如million级别的特征)
-
需要保证所有特征值的大小比例都差不多,否则收敛的时间会长很多
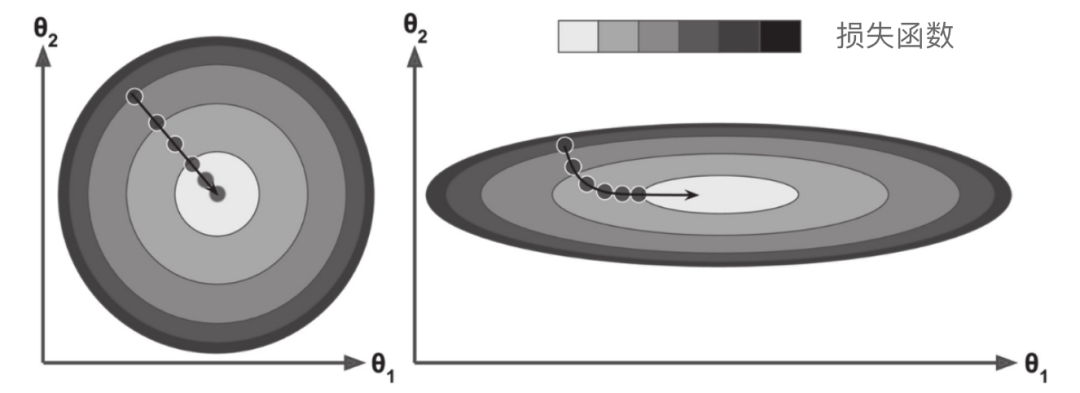
损失函数虽然是碗状的,但如果不同特征的尺寸差别巨大,那它可能是一个非常细长的碗。如图所示的梯度下降,左边的训练集上特征1和特征2具有相同的数值规模,而右边的训练集上,特征1的值则比特征2要小得多(注:因为特征1的值较小,所以θ1需要更大的变化来影响成本函数,这就是为什么碗形会沿着θ1轴拉长)