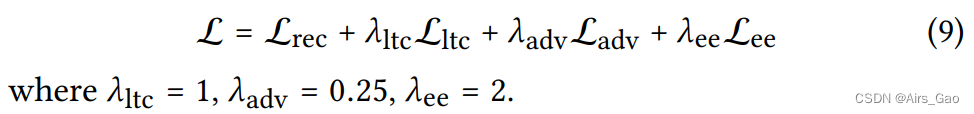旋转数组的最小数字——II

题目链接

注：此题是昨天旋转数组的最小数字——I的拓展延伸，昨天题目数组的条件是不会存在重复元素，而本题数组的元素可以重复，因此建议先做前面一题，进行思考，这样求解这一题的过程就会容易理解许多。

---

旋转数组的性质

由旋转数组的最小数字——I我们知道了：

以数组最右侧数据val为参考对象，最小值右侧的数一定小于val，最小值左边的数一定大于val

可以得到以下图像：

而今天这一题多了一个条件：数组中可能存在重复元素。我们需要考虑的情况又复杂了一点：

以数组最右侧数据val为参考对象，最小值右侧的数一定等于小于val，最小值左边的数一定大于等于val

我们同样用二分法来解决：

• 同样，我们设左边界为left，右边界为right，区间的中间下标为mid

• 如果nums[mid] > nums[right]，和原来一样，最小值一定不在左侧区域，left = mid + 1

• 如果nums[mid] < nums[right]，和原来一样，最小值一定不在右侧区域（但可能就是mid位置的值），right = mid

• 如果nums[mid]==nums[rihgt]，这种情况就值得注意了，如下图：

• 此时，nums[mid]可能在最小值的左边，也可能在最小值的右边，因此我们不能随意地舍去mid左侧的数据或者右侧的数据。对于这种情况的处理，我们有两种方法：

方法一：

不能随意舍去mid左半部分或者右半部分是因为最小值到底是在mid的左边还是右边是不确定的，但是如果我们可以通过处理来确定最小值和mid的关系呢？

我们知道，数组旋转后，其被分割成了两串非递减数列，而令我们困扰的就是诸如这种情况：[3,3,1,3]，[4,4,5,1,4,4,4,4,4]。那么我们可以删除数组前面所有等于nums[right]的元素，使数组变成诸如[1,3]，[5,1,4,4,4,4]的形式，这样当nums[mid]==nums[right]这种情况出现时，mid就一定会出现在最小值的右侧，mid右侧的数据也就可以删除了。

实现代码

int minArray(int* nums, int numsSize){
    int left = 0;
    int right = numsSize - 1;

    //删除数组前面所有等于nums[right]的元素
    while (left < numsSize && nums[left] == nums[right])
        left++;

    while (left < right)
    {
        int mid = (right - left) / 2 + left;

        //如果中间值大于最右边的值，那么最小值一定在中间值的右边
        if (nums[mid] > nums[right])
            left = mid + 1;
        //否则，最小值就在最右边的值的左边，也可能就是这个中间值
        else
            right = mid;
    }

    return nums[right];
}

方法二

虽然我们不能随意舍弃mid的左半部分或者右半部分，但是我们可以确定，无论nums[right]是不是最小值，都有它的一个替代品nums[mid]，因此我们可以删除最右边的数据nums[right]

实现代码

int minArray(int* nums, int numsSize){
    int left = 0;
    int right = numsSize - 1;

    while (left < right)
    {
        int mid = (right - left) / 2 + left;

        //如果中间值大于最右边的值，那么最小值一定在中间值的右边
        if (nums[mid] > nums[right])
            left = mid + 1;

        //如果中间值小于最右边的值，那么最小值一定在中间值的左边或者就是中间值
        else if (nums[mid] < nums[right])
            right = mid;

        //如果中间值等于最右边的值，那么就删除最右侧元素
        else    
            right--;
    }

    return nums[left];
}