oracle 代码测试数据

CREATE TABLE PRODUCT_CATEGORY
(	
   PRODUCT_CATEGORYID NUMBER(11,0) NOT NULL , 
   NAME VARCHAR2(255) NOT NULL ENABLE, 
   PRIMARY KEY (PRODUCT_CATEGORYID)
)


INSERT ALL
into PRODUCT_CATEGORY(PRODUCT_CATEGORYID, NAME)VALUES(2,'国学')
into PRODUCT_CATEGORY(PRODUCT_CATEGORYID, NAME)VALUES(3,'魔幻')
into PRODUCT_CATEGORY(PRODUCT_CATEGORYID, NAME)VALUES(4,'语文')
into PRODUCT_CATEGORY(PRODUCT_CATEGORYID, NAME)VALUES(5,'体育')
into PRODUCT_CATEGORY(PRODUCT_CATEGORYID, NAME)VALUES(7,'金融')
SELECT 1 FROM DUAL;


SELECT PRODUCT_CATEGORYID, NAME
FROM "C##ROOTUSER".PRODUCT_CATEGORY;

 

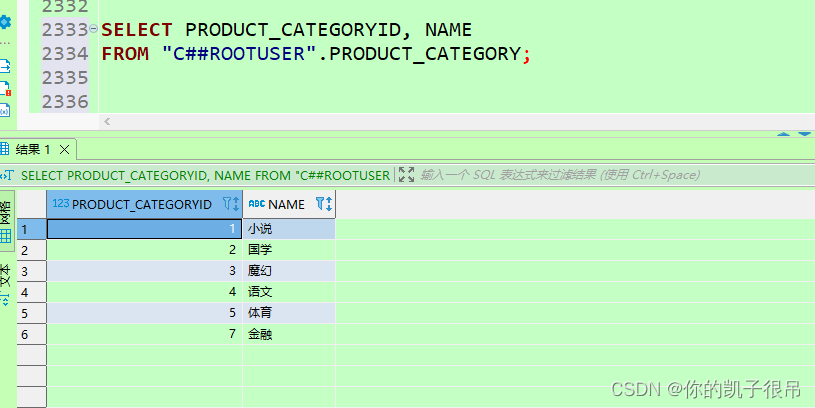
DM数据库表数据

 

 

快速上手 | 达梦技术文档