目录

题目：

示例：

分析：

代码：

---

题目：

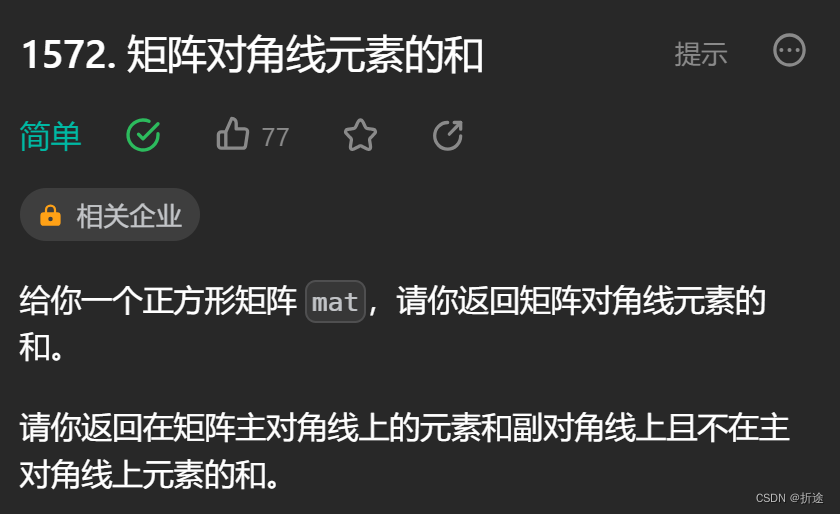
示例：

分析：

题目给我们一个矩阵，让我们把矩阵对角线上的元素都加起来返回。

那么矩阵的对角线是有两条的，一条是从左上到右下，另一条是从右上到左下。

我们先看第一条：

 可以看出来对角线上的元素下标是有规律的，他们的行下标和列下标是一样的，所以我们遍历n次，也就是矩阵的长度次。每次都加上mat[ i ][ i ]，这样就算是把从左上到右下这条对角线给解决了。

第二条从右上到左下：

 我们咋一看好像规律没有上一条这么明显，不过总还是有的，他们同一个元素的行下标与列下标相加总和是等于n-1的，所以我们仍然可以遍历n次，每次都加上mat[ i ][ n - i - 1 ]，这样就把从右上到左下的这条对角线也给解决了。

最后还有一个小问题，如果矩阵的长度为奇数，那么我们获取两条对角线上的元素时就会重复包含矩阵最中间的元素两次。

所以我们最后需要做一个判断，如果n为奇数，那么答案还需要再减去矩阵中心的数。

代码：

class Solution {
public:
    int diagonalSum(vector<vector<int>>& mat) {
        int res=0;
        int n=mat.size();
        for(int i=0;i<n;i++){
            res+=mat[i][i]+mat[i][n-i-1];
        }
        if(n%2==1) res-=mat[n/2][n/2];
        return res;
    }
};