全局优化函数简介

scipy的optimize模块非常强大，也是我个人使用最多的scipy模块，这里面封装的都是成熟且高效的算法，久经考验。对于参加数学竞赛的同学来说，辛辛苦苦撸出来的遗传算法、模拟退火算法，在scipy所实现的双退火或是差分进化算法面前，就显得十分稚嫩。

其中中封装了6个全局非线性优化函数，这些函数的统一要求是，得到一组值$x$，使得 func(x, *args) 的值达到最小。故而这些参数统一具备的输入参数是待优化函数func，除了basinhopping之外，都有args参数。

这六个函数分别是

• brute 即暴力求解，类似于穷举
• differential_evolution 差分进化算法，后文统称de
• basinhopping 盆地跳跃算法
• shgo算法 单形同调优化
• dual_annealing 双退火算法，后文统称da
• direct算法

其中，de, shgo, da, direct算法除了需要func之外，还要输入参数bounds，表示定义域区间。在brute函数中，区间参数为ranges，为非必要参数。而在basinhopping算法中，需要指定一个初值x0。

算法执行完成后，这些函数提供了一个接下来要执行的函数的接口，其中brute用参数finish，其他函数用callback来调用。

考虑到算法在执行过程中往往需要引入随机数，故而设置随机数种子有利于成果复现，在de, da以及basinhopping中提供了seed参数，用于设置随机数种子。

在搜索全局最优值时，不可避免地要考虑到局部的优化情况，从而调用局部最小值函数minimize，所以basinshopping, shgo, da函数提供了minimizer_kwargs参数，作为调用minimize时的参数字典。

任何算法至少都要有一个终止条件，其中最粗暴的条件就是最大迭代次数，de, da, direct这三个函数用参数maxiter来声明最大迭代次数； basinshopping中则用参数niter。

brute和de算法提供了多进程开关workers。

在brute, de, basinhopping中，提供了disp开关，当为True时，会打印算法运行中的某些信息。

详解

这六种算法的详细讲解见下表所示

算法	链接
brute	这个没什么好讲的
direct	矩形分割算法
de	差分进化算法
da	双模拟退火算法
basinhopping	跳盆算法
shgo算法	SHGO算法

性能测试

下面对五种非线性优化算法进行测试，测试函数为

$$y=\sum _{i=0}^8(i+1)\cos \frac{i{x}_i}{5}$$

写为Python程序为

import numpy as np
def test(xs):
    _sum = 0.0
    for i in range(len(xs)):
        _sum = _sum + np.cos((xs[i]*i)/5)*(i+1)
    return _sum

下面是测试代码

from time import time
import scipy.optimize as so

funcDct = {
"de": so.differential_evolution,
"basinhopping": so.basinhopping,
"shgo": so.shgo,
"da": so.dual_annealing,
"direct": so.direct,
}

bounds = [[0,15] for _ in range(8)]
x0 = [0 for _ in range(8)]

for key in funcDct:
    para = bounds if key!= "basinhopping" else x0
    t0 = time()
    ret = funcDct[key](test, para)
    msg = f"{key}算法耗时{time()-t0}，优化结果为：\n" 
    msg += ", ".join([f"{x:.4f}" for x in ret.x])
    msg += f"\nf(x)={ret.fun:.4f}"
    print(msg)

测试结果如下

---

de算法耗时0.595804，优化结果为：
5.9084, 15.0000, 7.8540, 5.2360, 3.9270, 3.1416, 13.0900, 6.7320
f(x)=-33.9800
basinhopping算法耗时1.666373，优化结果为：
-1.6063, -15.7080, -7.8540, -5.2360, 3.9270, 3.1416, 2.6180, -6.7320
f(x)=-34.0000
shgo算法耗时2.203928，优化结果为：
7.5000, 15.0000, 7.8540, 5.2360, 3.9270, 15.0000, 7.8540, 6.7320
f(x)=-32.5381
da算法耗时0.398701，优化结果为：
4.3058, 15.0000, 7.8540, 5.2359, 3.9270, 3.1416, 7.8540, 11.2200
f(x)=-33.9800
direct算法耗时0.009508，优化结果为：
7.5000, 14.9074, 7.8704, 5.2778, 11.7593, 3.0556, 2.6235, 2.2531
f(x)=-33.9494

---

列表如下

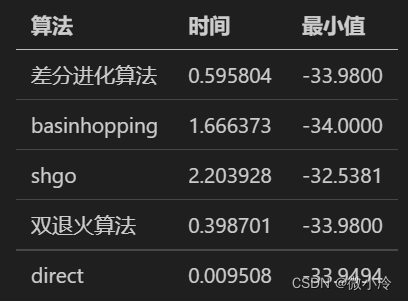
可见，direct算法最快，由于没有边界的限制，basinhopping得到了最优解，而其他函数表现各异，以差分进化算法和双退火算法表现最佳。