A 游游的数字圈
题目大意
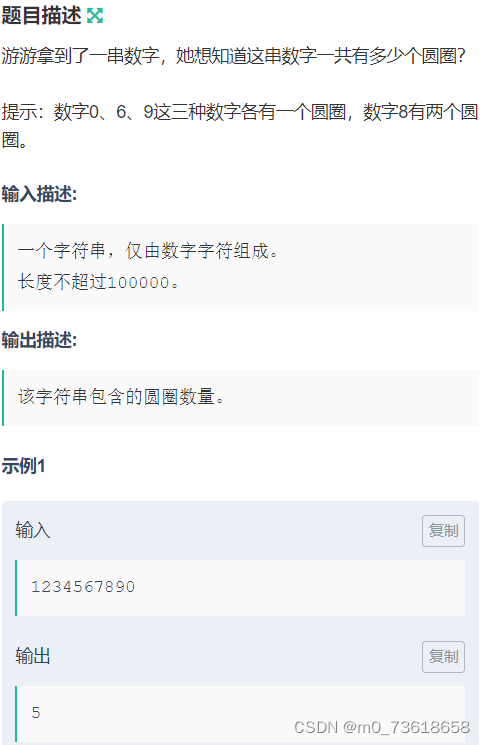
给定一个由数字字符组成的字符串,统计该字符串中出现的圆圈数量。其中数字0、6、9各有一个圆圈,数字8有两个圆圈。
思路分析
遍历字符串中的每个字符,对于每个字符,判断其是0、6、9则加1,是8则加2
时间复杂度
O(n)
AC代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
string s;
cin>>s;
int cnt=0;
for(char c:s)
{
if(c=='0'||c=='6'||c=='9'){
cnt++;
}else if(c=='8'){
cnt+=2;
}
}
cout<<cnt<<endl;
return 0;
}
B 竖式乘法
题目大意
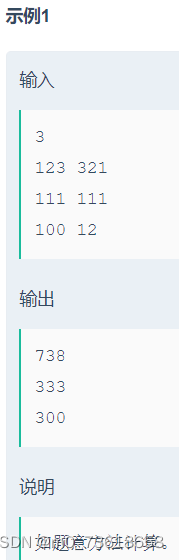
按照游游的竖式乘法计算a乘以b的值,并输出结果。
思路分析
游游给出的竖式乘法是一种按位相乘并相加的方法。对于每个位上的数,将a与b的对应位相乘,并将结果累加得到最终答案。
时间复杂度
O(t*m)
AC代码
#include<bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t--) {
int a;
string b;
cin >> a >> b;
long long res = 0;
for(char c : b) {
res += a * (c - '0');
}
cout << res << endl;
}
return 0;
}
C 游游的数值距离
题目大意
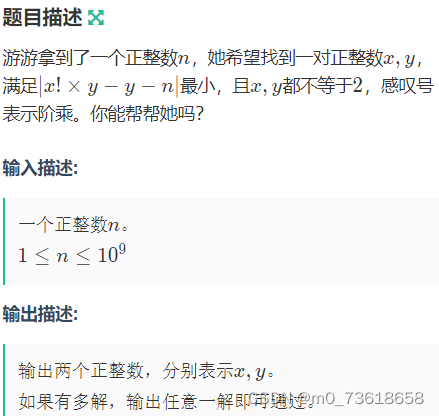
给定一个正整数n,找到一对正整数x和y,使得|x! × y - y - n|最小,并且x和y不能等于2。
思路分析
把式子整理一下可知,题目要求找到一个正整数x和一个正整数y,使得(x!-1)*y与输入的n的差值最小。知n,可以枚举x,因为x!会很大,算到15!左右即可。剩下一个未知数y,对于每个x,我们计算出y的三种可能取值:y=n/(x!-1),y=n/(x!-1)+1,y=n/(x!-1)-1。
因为题目要求使得(x!-1)*y与输入的n的差值最小。
- 在整数除法中,n/(x!-1) 已经是最小的可能值了。如果我们再减去1,那么 (x!-1)*(y-1) 的值会比 n 小得更多,这会使得 |x!×y-y-n| 的值变大,而不是变小。
所以只需要考虑 y=n/(x!-1) 和 y=n/(x!-1)+1 因为 y=n/(x!-1) 是 y 的最小可能值,而 y=n/(x!-1)+1 则是使得 (p-1)*y 的值刚好大于 n 的最小 y 值。所以只有这两种情况都可能使得 |x!×y-y-n| 的值最小。
时间复杂度
O(1)
AC代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
signed main()
{
int n;
cin >> n;
int p = 2, x = 1, y = 1, ans = n;
for(int i = 3; i <= 15; i++)
{
p *= i;
int y1 = n / (p - 1); // 计算商y1
if(abs((p - 1) * y1 - n) < ans && y1 != 2)
x = i, y = y1, ans = abs((p - 1) * y1 - n);
if(abs((p - 1) * (y1 + 1) - n) < ans && y1 + 1 != 2)
x = i, y = y1 + 1, ans = abs((p - 1) * (y1 + 1) - n);
}
cout << x << ' ' << y << endl;
return 0;
}
D 游游的k-好数组
题目大意
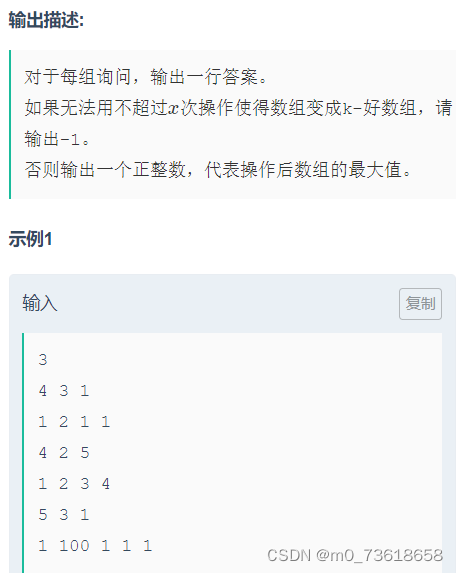
游游想要将一个大小为n的数组变成k-好数组,并且进行不超过x次操作。要求变换后的数组的最大值尽可能大。
思路分析
每个区间,滑动窗口每加一个t[i%k],就要减一个t[i%k],所以加和减要相等。记录每组元素中最大的元素为t[i%k]。
- 首先,可以将数组按照k的大小进行分组,每组的元素个数为n/k(如果n不能被k整除,那么前n%k组的元素个数为n/k+1)。
- 然后,计算每组的最大元素,并记录下来。同时,我们也计算出将每个元素变为其所在组的最大元素需要的操作次数,并累加起来。
- 如果累加的操作次数大于x,那么说明无法在不超过x次操作的情况下使得数组变为k-好数组,输出-1。
- 如果累加的操作次数小于等于x,那么我们可以继续增大每组的最大元素。将剩余的操作次数平均分配给每组,然后将每组的最大元素增大相应的值。
- 最后,数组的最大值就是所有组的最大元素中的最大值。
时间复杂度
O(n)
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int a[N],t[N];
void solve()
{
memset(t,0,sizeof t);
int n,k,x;
cin>>n>>k>>x;
for(int i=0;i<n;i++)
{
cin>>a[i];
t[i%k]=max(t[i%k],a[i]);
}
int cn=0;
for(int i=0;i<n;i++)
{
cn+=t[i%k]-a[i];
}if(x<cn)
{
cout<<-1<<"\n";
return;;
}
x-=cn;
int ans=0;
for(int i=0;i<k;i++)
{
int rest=n/k+(i<n%k);
ans=max(ans,t[i]+x/rest);
}
cout<<ans<<"\n";
}
signed main()
{
int t;
cin>>t;
while(t--)
{
solve();
}
return 0;
}
E 小红的循环节长度
题目大意
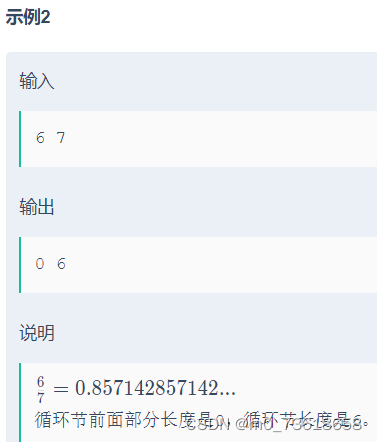
小红想知道一个分数的循环节前面部分的长度以及循环节的长度。给定两个正整数p和q,代表分子和分母。要求输出循环节前面部分的长度和循环节的长度。
思路分析
根据数学原理,一个分数可以表示为有限小数或无限循环小数。对于无限循环小数而言,循环节是必然存在的。通过欧拉函数和模运算,可以计算出循环节的长度。同时,通过化简分母为最简形式以及判断分数是否为有限小数,可以提前排除掉一部分情况,减少计算量。
- 首先判断给定的分数是否为有限小数。如果分母能够被2或5整除,则说明分数是有限小数,直接输出-1。
- 将分母化简为最简形式,并计算分母中包含2和5的个数,用c2和c5表示。
- 计算欧拉函数phi(q),得到与q互质的小于等于q的正整数个数。
- 遍历phi(q)的所有因子i,判断10i和10(phi(q)/i)在模q下是否为1,如果是则更新循环节长度mi为i或phi(q)/i的较小值。
- 输出max(c2, c5)作为循环节前面部分的长度,输出mi作为循环节的长度。
所用到的知识点和算法:
- 欧拉函数:用于计算与给定正整数互质的小于等于它的正整数个数。
- 快速幂算法:用于快速计算一个数的指定次幂,降低时间复杂度。
- 最大公约数:用于化简分数为最简形式。
- 模运算:用于判断10i和10(phi(q)/i)在模q下是否等于1。
时间复杂度
O(sqrt(q) * sqrt(phi(q)) * log(q))
AC代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
// 欧拉函数
int phi(int x) {
int res = x;
for (int i = 2; i <= x / i; i++) {
if (x % i == 0) {
res = res / i * (i - 1);
while (x % i == 0) x /= i;
}
}
if (x > 0) res = res / x * (x - 1);
return res;
}
// 快速幂模运算
int qmi(int a, int k,int p) {
__int128 res = 1;
while (k)
{
if (k & 1) res =(__int128) res * a%p;
a = (__int128)a*a%p;
k >>= 1;
}
return res;
}
// 求最大公约数
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
void solve() {
int p, q;
cin >> p >> q;
// 约分并计算分母中包含的因子个数
q /= gcd(p, q);
int c2 = 0, c5 = 0;
while (q % 2 == 0) q /= 2, c2++;
while (q % 5 == 0) q /= 5, c5++;
// 判断是否为有限小数
if (q == 1) {
cout << -1;
return;
}
// 求解循环节前面部分长度和循环节长度
int te= phi(q);
int mi = 1e18;
for (int i = 1; i <= te/ i; i++) {
if (te% i == 0) {
if (qmi(10, i, q) == 1)mi = min(mi, i);
if (qmi(10, te/ i, q) == 1) mi = min(mi, te/ i);
}
}
cout << max(c2, c5) << ' ' << mi;
}
signed main() {
solve();
return 0;
}