为什么有人夜里碰到股票问题,辗转反侧睡不着觉?为什么有人看到股票问题心理欢喜直接操作?你是想做哪类人?今天就揭秘股票问题,让你应对股票问题的时候可以如鱼得水。
这种问题一看就是动态规划问题,动态规划说难听一点就是穷举,但是我们应该如何的去聪明的穷举,这是我们需要考虑的
给定一个数组,它的第
i个元素是一支给定的股票在第i天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
股票l只是进行了一次交易,相当于k=1;股票II相当于不限制交易次数,k=inf;股票III只是进行了2次交易,相当于k=2;剩下的题目也是不限次数,但是增加了一些额外的条件,其实解题步骤也是大差不差的,好了,我们言归正传,开始我们的解密之旅
动态规划的核心就是状态和转移(选择),首先,我们看这道题,它一天中可能有几种状态,它的每种状态又有几种可能,我们要根据状态去找出相对应的选择,我们是不是要穷举所有的状态,然后在根据选择去更新状态,看下列穷举的模板:
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 择优(选择1,选择2...)每天都有3种选择:买入、卖出、无操作,我们简单的用buy、sell、none表示这三种选择
但是这买卖还有其他条件的限制,sell必须在buy的后面,buy的前提是k>0(还可以操作的次数),none也可以分为两种状态:一种是持有股票进行,一种是没有持有股票进行,这几种情况才是比较难想的,但是想到了以后,这种题就迎难而解了
那么我们现在这个问题的状态总共有3个,一个是天数、一个是可以操作的次数、一个是是否持有股票,我们用代码来展示一下:
dp[i][k][0 or 1];
0<=i<=n-1 1<=k<=K;
n为天数,大K为交易的上限,0和1代表的是是否持有股票然后我们根据穷举的模板就能写出得出:
for(int i=0;i<n;i++){
for (int k = 1; k <=K; k++) {
for(int s=0;s<2;s++){
dp[i][k][s]=max(buy,sell,none);
}
}
}我们现在想要求的是dp[n-1][K][0]的值,含义就是在最后一天,最多允许K次交易,最多可以获得多少的利润
现在的穷举的框架已经给了,接下来状态进行进行转移呢?
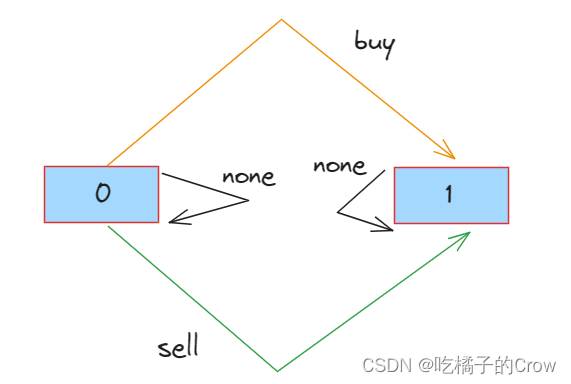
通过这个图我们可以很清楚的看到,每种状态是如何转移而来的,我们试着写一写状态转移方程
dp[i][k][0]=max(dp[i-1][k][0]),dp[i-1][k][1]+prices[i])
max( 选择了无操作 选择了卖出 )dp[i][k][0]:我今天没有持有股票,最大的交易次数为k,可以推出昨天的情况:
- dp[i-1][k][0]:昨天就没有持有股票,截止昨天为止最大的交易次数还是k
- dp[i-1][k][1]+prices[i]:昨天持有股票,截止昨天最大交易数限制为k,今天进行了sell
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
max( 今天选择 none, 今天选择 buy )dp[i][k][1]:我今天持有股票,最大的交易次数为k,那么我们就可以推出昨天的情况:
- dp[i-1][k][1]:我昨天就持有股票,截止昨天的最大交易次数为k,今天进行了none
- dp[i-1][k-1][0]-prices[i]:我昨天没有持有,截止昨天的最大交易次数为k-1,我今天选择了buy
现在我们已经完成了最艰难的一步了,如果之前的内容你都可以理解,恭喜你,你已经可以解决这类型问题了,看究极模板:
dp[-1][...][0] = 0
解释:因为 i 是从 0 开始的,所以 i = -1 意味着还没有开始,这时候的利润当然是 0。
dp[-1][...][1] = -infinity
解释:还没开始的时候,是不可能持有股票的。
因为我们的算法要求一个最大值,所以初始值设为一个最小值,方便取最大值。
dp[...][0][0] = 0
解释:因为 k 是从 1 开始的,所以 k = 0 意味着根本不允许交易,这时候利润当然是 0。
dp[...][0][1] = -infinity
解释:不允许交易的情况下,是不可能持有股票的。
因为我们的算法要求一个最大值,所以初始值设为一个最小值,方便取最大值。将上图的状态转移方以及base进行总结得到:
base case:
dp[-1][...][0] = dp[...][0][0] = 0
dp[-1][...][1] = dp[...][0][1] = -infinity
状态转移方程:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
当数组中的k不会发生改变时,我们可以省略掉k
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])这道题最大的操作数是2,所以k对结果的影响是不能被忽略掉的,所以我们单套模板的话,会直接超时,所以我们要对代码进行改进,穷举k的每种状态,再进行选择
//买卖股票
int[][] dp;
public int maxProfit(int[] prices) {
//对入参进行判断
if (prices == null || prices.length == 0) {
return 0;
}
//最大操作数是2
int maxK=2;
int n=prices.length;
int[][][] dp=new int[n][maxK+1][2];
for(int i=0;i<n;i++){
//穷举k的每一种状态
for(int k=maxK;k>=1;k--){
//因为下面是[i-1],i是从0开始的,所以i-1=-1的情况是存在的
if(i-1==-1){
//处理i=0的时候的base情况
dp[i][k][0]=0;
dp[i][k][1]=-prices[i];
continue;
}
//持有股票
dp[i][k][1]=Math.max(dp[i-1][k][1],dp[i-1][k-1][0]-prices[i]);
//无股票
dp[i][k][0]=Math.max(dp[i-1][k][0],dp[i-1][k][1]+prices[i]);
}
}
return dp[n-1][maxK][0];
}这道题就讲解完了,你对股票问题是否有了不一样的收获,这道题的关键还是在聪明的穷举出所有的可能的状态,基于base的基础上慢慢的向后推进,相信你有举一反三的能力,其他题也和这道题的解题方法几乎差不多,