0095 贪心算法，普利姆算法

import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;

/*
* 贪心算法
* 1.指在对问题进行求解时，在每一步选择中都采取最好或最优的选择，希望能够导致结果是最好或最优的算法
* 2.所得到的结果不一定是最优结果，但相对接近最优解
*
* 应用——集合覆盖
* 存在下列广播台及可覆盖地区，如何选择最少的广播台？
* 广播台           覆盖地区
* K1           北京，上海，天津
* K2           广州，北京，深圳
* K3           成都，上海，杭州
* K4           上海，天津
* K5           杭州，大连
*
* 思路
* 1.使用穷举法列出每个可能的广播台集合
* 假设有n个广播台，则组合共有2^n-1，效率低
*
* 2.使用贪心算法，得到近似解，效率高
*        1.遍历所有广播电台，找到一个覆盖了最多未覆盖地区的电台
*        2.将这个电台加入到一个集合中（如ArrayList），把该电台覆盖的地区在下次比较中去掉
*        3.重复1，直到覆盖全部地区
*/
public class Greedy_ {
   public static void main(String[] args) {
       //创建广播电台K-V，放入Map
       HashMap<String, HashSet<String>> broadcasts = new HashMap<String,HashSet<String>>();
       //将各个电台放入到broadcasts
       HashSet<String> hashSet1 = new HashSet<String>();
       hashSet1.add("北京");
       hashSet1.add("上海");
       hashSet1.add("天津");

       HashSet<String> hashSet2 = new HashSet<String>();
       hashSet2.add("广州");
       hashSet2.add("北京");
       hashSet2.add("深圳");

       HashSet<String> hashSet3 = new HashSet<String>();
       hashSet3.add("成都");
       hashSet3.add("上海");
       hashSet3.add("杭州");

       HashSet<String> hashSet4 = new HashSet<String>();
       hashSet4.add("上海");
       hashSet4.add("天津");

       HashSet<String> hashSet5 = new HashSet<String>();
       hashSet5.add("杭州");
       hashSet5.add("大连");

       //加入到map
       broadcasts.put("K1", hashSet1);
       broadcasts.put("K2", hashSet2);
       broadcasts.put("K3", hashSet3);
       broadcasts.put("K4", hashSet4);
       broadcasts.put("K5", hashSet5);

       //存放所有的地区
       HashSet<String> allAreas = new HashSet<String>();
       allAreas.add("北京");
       allAreas.add("上海");
       allAreas.add("天津");
       allAreas.add("广州");
       allAreas.add("深圳");
       allAreas.add("成都");
       allAreas.add("杭州");
       allAreas.add("大连");

       //创建ArrayList，存放选择电台集合
       ArrayList<String> selects = new ArrayList<String>();

       //定义临时集合，在遍历过程中，存放遍历中的电台覆盖地区和当前没有覆盖地区的交集
       HashSet<String> tempSet = new HashSet<String>();

       //定义maxKey，保存遍历中能够覆盖最多未覆盖地区对应电台的key
       //如果maxKey不为null，加入到selects
       String maxKey = null;

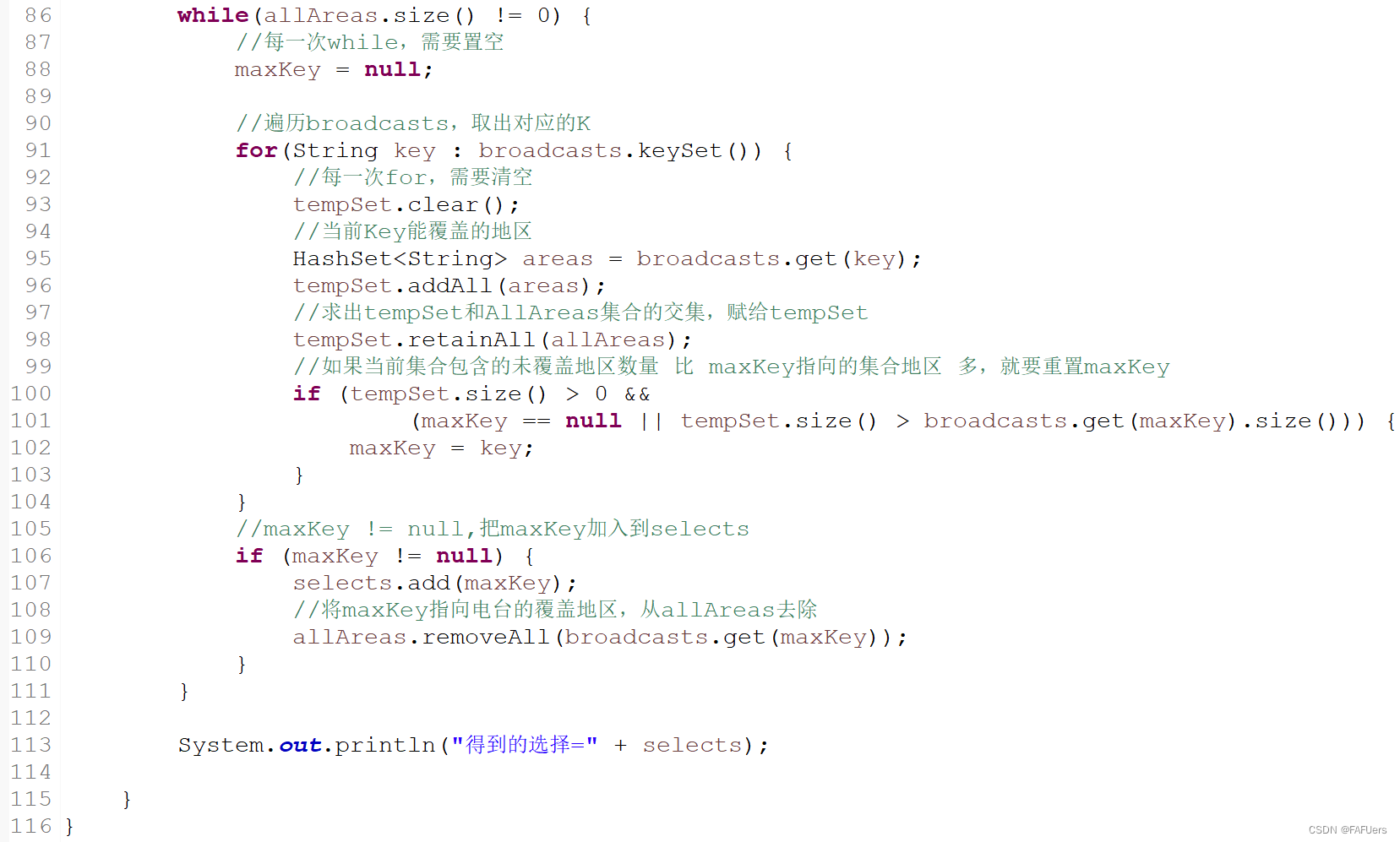
       while(allAreas.size() != 0) {
           //每一次while，需要置空
           maxKey = null;

           //遍历broadcasts，取出对应的K
           for(String key : broadcasts.keySet()) {
               //每一次for，需要清空
               tempSet.clear();
               //当前Key能覆盖的地区
               HashSet<String> areas = broadcasts.get(key);
               tempSet.addAll(areas);
               //求出tempSet和AllAreas集合的交集，赋给tempSet
               tempSet.retainAll(allAreas);
               //如果当前集合包含的未覆盖地区数量比 maxKey指向的集合地区多，就要重置maxKey
               if (tempSet.size() > 0 &&
                       (maxKey == null || tempSet.size() > broadcasts.get(maxKey).size())) {
                   maxKey = key;
               }
           }
           //maxKey != null,把maxKey加入到selects
           if (maxKey != null) {
               selects.add(maxKey);
               //将maxKey指向电台的覆盖地区，从allAreas去除
               allAreas.removeAll(broadcasts.get(maxKey));
           }
       }

       System.out.println("得到的选择=" + selects);

   }
}

import java.util.Arrays;
/*
* 普利姆算法
*
* 应用——修路问题
* 尽可能选择少的路线，并且每条路线最小，保证总里程数最小
*
* 本质：最小生成树（MST）
* 1.给定一个带权的无向连通图，使树上所有边权的总和最小，就叫最小生成树
* 2.N个顶点，N-1条边，包含所有顶点
* 3.求最小生成树的算法主要为普利姆算法和克鲁斯卡尔算法
*
* 普利姆算法求最小生成树，就是在包含n个顶点的连通图中，找出只要n-1条边包含所有n个顶点的连通子图，即极小连通子图
* 算法如下：
* 1.设G=（V,E）是连通网，T=(U,D)是最小生成树，V,U是顶点集合，E,D是边集合
* 2.若从顶点u开始构造最小生成树，则从集合V中取出顶点u放入集合U中，标记顶点v的visited[u]=1
* 3.若集合U中顶点ui与集合V-U中的顶点vj之间存在边，则寻找这些边中权值最小的边，但不能构成回路
*    将顶点vj加入集合U中，将边（ui，vj）加入集合D中，标记visited[vj]=1
* 4.重复步骤2，直到U,V相等，即所有顶点都被标记为访问过，此时D中有n-1条边
*/
public class Prim_ {
   public static void main(String[] args) {
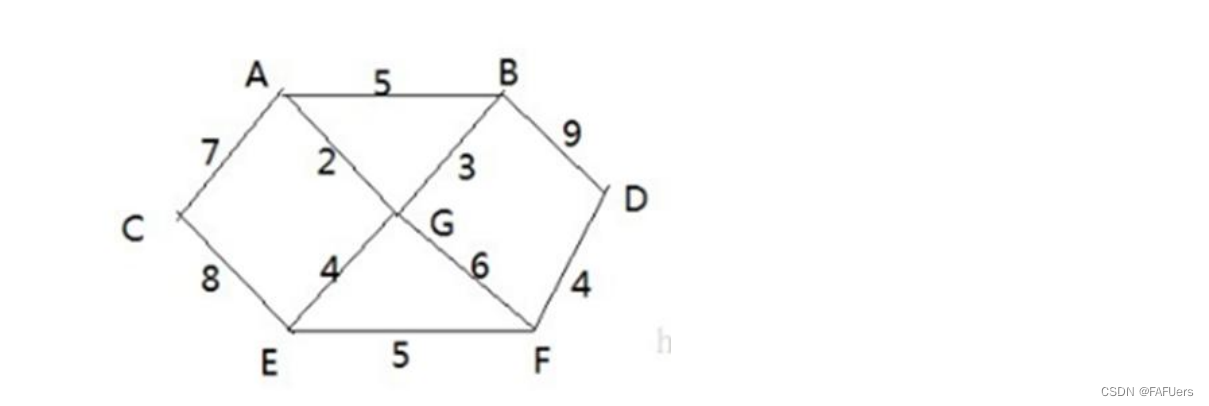
       char[] data = new char[] {'A','B','C','D','E','F','G'};
       int verxs = data.length;
       //邻接矩阵关系用二维数组表示,10000表示两个点不连通
       int[][] weight = new int[][] {
           {10000,5,7,10000,10000,10000,2},
           {5,10000,10000,9,10000,10000,3},
           {7,10000,10000,10000,8,10000,10000},
           {10000,9,10000,10000,10000,4,10000},
           {10000,10000,8,10000,10000,5,4},
           {10000,10000,10000,4,5,10000,6},
           {2,3,10000,10000,4,6,10000}};

       //创建Graph对象
       MGraph graph = new MGraph(verxs);
       //创建一个MinTree对象
       MinTree minTree = new MinTree();
       minTree.creatGraph(graph, verxs, data, weight);
       //输出
       minTree.showGraph(graph);

       //普利姆算法
       minTree.prim(graph, 0);
   }
}

//创建最小生成树
class MinTree{
   //创建图的邻接矩阵
   //graph:图对象，verxs：图对应的顶点个数，data：图的各个顶点的值，weight：图的邻接矩阵
   public void creatGraph(MGraph graph,int verxs,char data[],int[][] weight) {
       for(int i = 0;i < verxs;i++) {//顶点
           graph.data[i] = data[i];
           for(int j = 0;j < verxs;j++) {//邻接矩阵
               graph.weight[i][j] = weight[i][j];
           }
       }
   }

   //显示图的邻接矩阵
   public void showGraph(MGraph graph) {
       for(int[] link : graph.weight) {
           System.out.println(Arrays.toString(link));
       }
   }

   //编写普利姆算法，得到最小生成树
   //graph:图，v:表示从图的第几个顶点开始生成 'A'->0,'B'->1...
   public void prim(MGraph graph,int v) {
       //visited[]标记结点是否被访问过
       int visited[] = new int[graph.verxs];
       //默认元素都是0，表示没有访问过
       for(int i = 0;i < graph.verxs;i++) {
           visited[i] = 0;
       }

       //把当前这个结点标记为已访问
       visited[v] = 1;
       //h1和h2记录两个顶点的下标
       int h1 = -1;
       int h2 = -1;
       int minWeight = 10000;//先初始成一个大数

       for(int k = 1;k < graph.verxs;k++) {//有graph.verxs个顶点，有graph.verxs-1条边

           //确定每一次生成的子图哪个结点和这次遍历的结点距离最近
           for(int i = 0;i < graph.verxs;i++) {//i结点表示被访问过的结点
               for(int j = 0;j < graph.verxs;j++) {//j结点表示没有被访问过的结点
                   if (visited[i] == 1 && visited[j] == 0 && graph.weight[i][j] < minWeight) {
                       //替换minWeight（权值最小的边）
                       minWeight = graph.weight[i][j];
                       h1 = i;
                       h2 = j;
                   }
               }
           }
           //退出for循环，找到了一条边最小
           System.out.println("边<" + graph.data[h1] + "," + graph.data[h2] + "> 权值：" + minWeight);
           //将当前结点标记为访问过
           visited[h2] = 1;
           //重置minWeight
           minWeight = 10000;
       }
   }
}

//图
class MGraph{
   int verxs;//表示图的结点个数
   char[] data;//存放结点数据
   int[][] weight;//邻接矩阵

   public MGraph(int verxs) {
       this.verxs = verxs;
       data = new char[verxs];
       weight = new int[verxs][verxs];
   }
}