概念:
通过两个指针,不断的调整区间,从而求出问题最优解的算法就叫“尺取法”,由于利用的是两个双指针,所以也叫作“双指针”算法,这里的“尺”的含义,主要是因为这类问题,最终要求解的都是连续的序列(子串),就好比一把尺子,故而得名
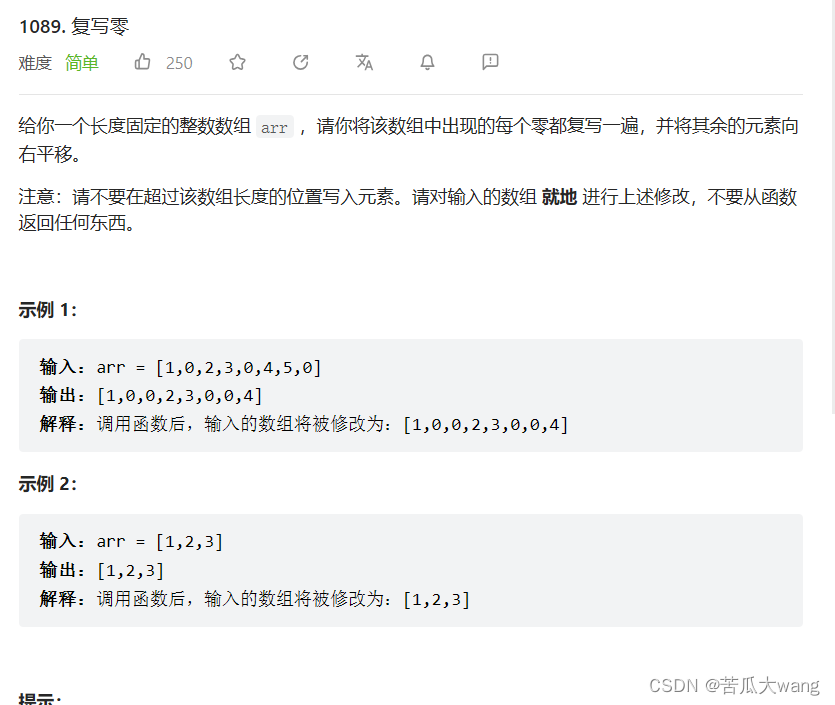
1.最长不重复子串
给定一个字符串
s,请你找出其中不含有重复字符的 最长子串 的长度。
1.初步分析
- n<=10^7;
- 最长
- 所有的字符不重复
- 子串
根据上面的几个关键词,我们可以得出一些结论,首先,根据n的范围已经能大致确认这是一个需要O(n)或者O(nlongn)的算法才能解决这个问题;其次,“最长”这个词告诉我们,可能是一个动态规划问题或者是贪心问题,判断字符是否重复可以用hash表在O(1)的时间内进行判断,最后枚举所有的子串是O(n^2)的
2.朴素算法
用max记录我们所需要的最大不重复子串的长度,用一个hash表代表某个字符是否出现过,算法的描述如下:
1.枚举子串的右端点i=0~n-1;
2.当hash表中出现hash[i]>1的时候,相当于双指针指向的区域范围内出现了重复字符,然后移动左指针,直到移出重复字符的时候,对指针区域长度求值,不断的移动,直到找到最大的无重复子串
public int lengthOfLongestSubstring(String s) {
if (s == null || s.length() == 0) {
return 0;
}
int left=0;
int max=0;
//将字符串转换为char
char[] str=s.toCharArray();
int[] hash=new int[128];
for(int right=0;right<s.length();right++){
char c=str[right];
hash[c]++;
while(hash[c]>1){
hash[str[left++]]--;
}
int val=right-left+1;
max=Math.max(val,max);
}
return max;
} 下面附一张不断枚举左端点的动态图,方便大家理解记忆(如果枚举左端点的话,最后还有额外的去判断是否越界,枚举右端点则不需要)
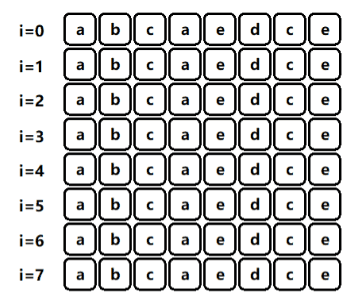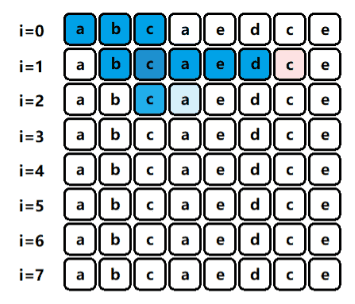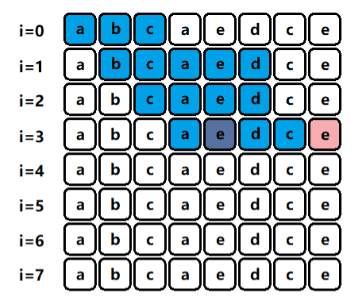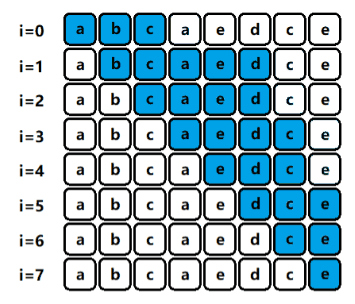

当区间内[i,j]中存在重复(红色)字符时,左指针i自增;否则右指针j自增,这部分大家可以自行下去尝试
2.算法描述
算法描述如下:
1.初始化i=0 j=i-1 代表一开始“尺子”的长度为0;
2.增长“尺子”的长度,即j=i+1;
3.判断当前这把“尺子”[i,j]是否满足题目给出的条件
1.如果满足,记录最优解
2.如果不满足,则减少“尺子”长度,缩小左端点 i=i+1 再次判断是否符合条件
满足条件时,j++,不满足条件时,i++;
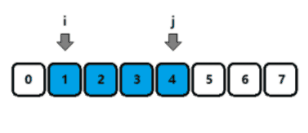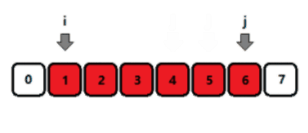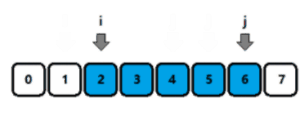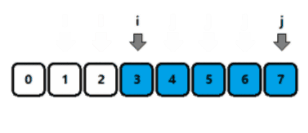
双指针满足的前提条件:
- 单调性
举个栗子:[2 6 9 5 12 5] 这种数组可以用双指正解决么?每次移动它的情况是不确定的
任意一个指指针的增加,条件满足与否只会出现两种情况,即:
满足—>不满足或者是不满足—>满足,不会出现 满足—>不满足—>满足
- 时效性
必须要在O(1)或者O(log2n)的时间内,求出当前区间[i,j]是否满足既定条件,否则无法用这种算法进行求解
leetcode题单:
反转字符串
public void reverseString(char[] s) {
int i=0;
int j=s.length-1;
while(i<j){
char temp=s[i];
s[i]=s[j];
s[j]=temp;
i++;
j--;
}
}判断子序列
public boolean isSubsequence(String s, String t) {
if(s==null||t==null){
return false;
}
int i=0;
int j=0;
while(i<s.length()&&j<t.length()){
if(s.charAt(i)==t.charAt(j)){
i++;
j++;
}else{
j++;
}
}
return i==s.length();
}两数之和
public int[] twoSum(int[] nums, int target) {
int[] num = new int[2];
if (nums == null || nums.length == 0) return num;
int left=0;
int right=nums.length-1;
Arrays.sort(nums);
while(left<right){
if(nums[right]+nums[left]==target){
num[0]=left;
num[1]=right;
return num;
}else if(nums[right]+nums[left]<target){
left++;
}else{
right--;
}
}
return num;
}无重复字符的最长子数组
public int lengthOfLongestSubstring(String s) {
if (s == null || s.length() == 0) {
return 0;
}
int left=0;
int max=0;
//将字符串转换为char
char[] str=s.toCharArray();
int[] hash=new int[128];
for(int right=0;right<s.length();right++){
char c=str[right];
hash[c]++;
while(hash[c]>1){
hash[str[left++]]--;
}
int val=right-left+1;
max=Math.max(val,max);
}
return max;
} 统计公平对的数目
public long countFairPairs(int[] nums, int lower, int upper) {
//同向双指针
Arrays.sort(nums);
long count = 0;
for (int i = 0; i < nums.length; i++) {
int num = nums[i];
//upper-num+1意思就是大于这个目标值的最左侧,右端是不包含
int m = nearIndex(nums, 0, i, upper - num + 1);
//lower-num意思就是大于lower-num的最左侧,左端是包含的
int n = nearIndex(nums, 0, i, lower - num);
count += m - n;//左闭右开
}
return count;
}
//二分搜索最左侧
public int nearIndex(int[] nums, int left, int right, int target) {
if (left >= right) {
return left;
}
int i = left;
int j = right;
while (i < j) {
int mid = i + (j - i) / 2;
if (nums[mid] >= target) {
j = mid;
} else {
i = mid + 1;
}
}
return i;
}