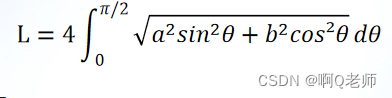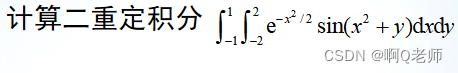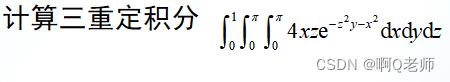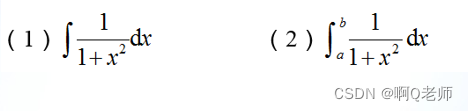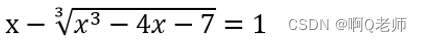数值积分

数值积分，用于求定积分的近似值。在数值分析中，数值积分是计算定积分数值的方法和理论。在数学分析中，给定函数的定积分的计算不总是可行的。许多定积分不能用已知的积分公式得到精确值。数值积分是利用黎曼积分等数学定义，用数值逼近的方法近似计算给定的定积分值。借助于电子计算设备，数值积分可以快速而有效地计算复杂的积分。

定积分的数值求解实现

定积分的数值求解介绍以下三种方法：自适应积分算法、梯形积分法与累计梯形积分。

自适应积分算法

基于全局自适应积分算法的integral函数用于求定积分。
调用格式：
q = integral(@fun,xmin,xmax)
q = integral(@fun,xmin,xmax,Name,Value)
其中，fun是被积函数，xmin和xmax分别是定积分的下限和上限。

示例：
人造地球卫星的轨迹可视为平面上的椭圆。我国第一颗人造卫星近地点距离地球表面439km，远地点距离地球表面2384km，地球半径为6371km，求该卫星的轨迹长度。

%求解：
>> a = 8755; 
>> b = 6810;
>> format long
>> funLength = @(x)sqrt(a^2.*sin(x).^2+ b^2.*cos(x).^2);
>> L = 4*integral(funLength, 0, pi/2)
L =
   4.908996526868900e+04
   

梯形积分法

离散数据用梯形法函数trapz求定积分。
调用格式：
（1）T = trapz(Y)，其中，用于求均匀间距的积分。通常，Y是向量，采用单位间距（即间距为1），计算Y的近似积分；若Y是矩阵，则输出参数T是一个行向量，T的每个元素分别存储Y的每一列的积分结果。
（2）T=trapz(X, Y)，其中，用于求非均匀间距的积分。X、Y满足函数关系Y = f(X)， 按X指定的数据点间距，对Y求积分。

示例：
从地面发射一枚火箭，表7.2记录了0~80秒火箭的加速度。试求火箭在第80秒时的速度。

%求解：
>> t = 0:10:80;
>> a = [30.00,31.63,33.44,35.47,37.75,40.33,43.29,46.69,50.67];
>> v = trapz(t,a)
v =
   3.0893e+03
   

累计梯形积分

函数cumtrapz用于对数据积分逐步累计。
调用格式：
（1）Z = cumtrapz(Y)，用于求均匀间距的累计积分。
（2）Z = cumtrapz(X,Y)，用于求非均匀间距的累计积分。

示例：
从地面发射一枚火箭，表7.2记录了0~80秒火箭的加速度。试求火箭在第80秒时的速度。

%求解：
>> v = cumtrapz(t,a)
>> v = cumtrapz(t,a)
v =
   1.0e+03 *
  1 至 7 列
         0    0.3081    0.6335    0.9780    1.3442    1.7346    2.1526
  8 至 9 列
    2.6026    3.0894
    

多重定积分的数值求解实现

integral2、quad2d函数用于求二重积分的数值解；integral3函数用于求三重积分的数值解。
调用格式：
q = integral2(fun,xmin,xmax,ymin,ymax,Name,Value)
q = quad2d(fun, xmin,xmax,ymin,ymax,)
[q,errbnd] = quad2d(fun, xmin,xmax,ymin,ymax, Name,Value)
q = integral3(fun,xmin,xmax,ymin,ymax,zmin,zmax)
q = integral3(fun,xmin,xmax,ymin,ymax,zmin,zmax,Name,Value)
其中，fun为被积函数，[xmin, xmax]为x的积分区域，[ymin, ymax]为y的积分区域，[zmin, zmax]为z的积分区域，选项Name的用法及可取值与函数integral相同。输出参数q返回积分结果，errbnd用于返回计算误差。

示例1：

示例2：

%求解1：
>> fxy = @(x,y) exp(-x.^2/2).*sin(x.^2+y);
>> I = integral2(fxy,-2,2,-1,1)
I =
    1.5745

%求解2：
>> fxyz = @(x,y,z)4*x.*z.*exp(-z.*z.*y-x.*x);
>> I3 = integral3(fxyz,0,pi,0,pi,0,1)
I3=
    1.7328
    

符号计算

符号计算又称计算机代数，通俗地说就是用计算机推导数学公式，如对表达式进行因式分解、化简、微分、积分、解代数方程、求解常微分方程等。

符号对象及其运算

1.建立符号变量
sym函数一次只能定义一个符号变量， syms函数一次可以定义多个符号变量。
调用格式为：
syms var1 … varN，其中，var1、 … 、varN为变量名，多个符号变量用空格分隔。
2.建立符号表达式
使用已经定义的符号变量组成符号表达式

%示例：
>> syms x y; 
>> f = 8*x^8-8*y+8*x*y
f =
   8*x^8 + 8*x*y - 8*y 
   

符号微积分

微积分（Calculus），数学概念，是高等数学中研究函数的微分(Differentiation)、积分(Integration)以及有关概念和应用的数学分支。它是数学的一个基础学科，内容主要包括极限、微分学、积分学及其应用。其中，微积分的符号是 ∫ 。

符号极限

函数limit用于求符号表达式极限。
调用格式：
limit(f, var, a, direction)
其中，计算当自变量var趋近于常数a时，符号表达式f的极限值；
选项var缺省时，按默认方式确定自变量；
选项a缺省时，求自变量趋近于0时，表达式f的极限值；
选项direction用于指定趋近的方向，'right’表示自变量从右边趋近于a，'left’表示自变量从左边趋近于a。

示例：求下列极限

%求解极限1:
>> syms x h t
>> limit((sin(x+h)-sin(x))/h, h, 0) 		
ans =
   cos(x)

%求解极限2:
>> limit((1+t/x)^x,inf) 		
ans =
   exp(t)

%求解极限3:
>> limit(x*(sqrt(x^2+1)-x),x,inf,'left') 		
ans =
   1/2

%求解极限4:
>> limit(cot(x)^(1/log(x)),x,0,'right') 		
ans =
   exp(-1)

符号导数

diff函数用于对符号表达式和符号函数求导。
调用格式：
diff(F,var,n)，其中，F是符号表达式或符号函数；选项var指定自变量，缺省时，按默认规则确定自变量；选项n指定求n阶导数，默认为1，即求一阶导数。
diff(F,var1,…,varN)，对多个自变量的求导的格式。

示例：求下列函数的导数

%求解1：
>> syms x;
>> diff(cos(x*x))               
ans =
   -2*x*sin(x^2)
%求解x的二阶导数：
>> diff(cos(x*x),x,2)      
ans =
   - 2*sin(x^2) - 4*x^2*cos(x^2)
%求解x的三阶导数：
>> diff(cos(x*x),x,3)      
ans =
   8*x^3*sin(x^2) - 12*x*cos(x^2)

%求解2：
>> syms a b t
>> fx = a*(t-sin(t));
>> fy = b*(1-cos(t));
%求对x的一阶导数  
>> diff(fy,t)/diff(fx,t)  	
ans =
   -(b*sin(t))/(a*(cos(t) - 1))


%求解3：
>> syms x y
>> diff(x^6-3*y^4+2*x^2*y^2,x)   %求对x的偏导数
ans =
   6*x^5 + 4*x*y^2
>> diff(x^6-3*y^4+2*x^2*y^2,y)        %求对y的偏导数
ans =
   4*x^2*y - 12*y^3
>> diff(x^6-3*y^4+2*x^2*y^2,x,y)
ans =
   8*x*y

求不定积分

1.int(expr, v)用于求不定积分，其中，以v为自变量，对符号表达式expr求不定积分。
2.int(expr, v, a, b) 或 int(expr, v, [a, b])用于求定积分，其中，以v为自变量，对符号表达式expr求定积分。a、b分别表示定积分的下限和上限。当表达式s关于变量x在闭区间[a，b]上可积时，函数返回一个定积分结果；当a、b中有一个是inf时，函数返回一个广义积分；当a、b中有一个符号表达式时，函数返回一个符号函数。

示例：分别求下列积分

%求解不定积分1：
>> syms x a b
>> f = 1/(1+x^2);
>> f1 = int(1/(1+x^2))        			
f1 =
   atan(x)

%求解定积分2：
>> f2 = int(1/(1+x^2),a,b)   			
f2 =
   atan(b) - atan(a)

符号方程求解

函数solve用于求解用符号表达式表示的代数方程。
调用格式：
Y = solve(s,v, Name,Value) ，其中，求解符号表达式s的代数方程，求解变量为v。v缺省时，按默认规则确定自变量。
Y = solve(s1,s2, …,sn,v1,v2,…,vn)
[y1,y2,…,yn] = solve([s1,s2, …,sn],[v1,v2,…,vn])
其中，求解符号表达式s1，s2，…，sn组成的代数方程组，自变量分别为v1，v2，…，vn。
选项Name和Value成对使用，用于设置求解过程的参数。

示例：求解下列方程

%求解：

>> syms x
>> y = solve(x-(x^3-4*x-7)^(1/3) == 1,x)		
y =
   3
   

函数dsolve用于求解常微分方程eqn在初值条件cond下的特解。若没有给出初值条件cond，则求方程的通解。eqn可以是符号等式或由符号等式组成的向量。
调用格式：
S = dsolve(eqn,cond)
S = dsolve(e,c,Name,Value)，其中，Name和Value成对使用，用于设置求解过程的参数。

示例：求下列微分方程的解

%求解1：
>> syms f(x)
>> y3 = dsolve(x*diff(y,x,2)-3*diff(y,x) == x^2, y(1) == 0, y(5) == 0)
y3 =
   (31*x^4)/468 - x^3/3 + 125/468

%求解2：
>> syms x(t) y(t)
>> [x,y] = dsolve(diff(x,t) == 4*x-2*y, diff(y,t) == 2*x-y)        	
x =
   C11/2 + 2*C10*exp(3*t)
y =
   C11 + C10*exp(3*t)