目录

一、信息存储：

1. 空间大小定义

2. 不同进制的转换方法

3. 各种数据类型所占字节数

4. 字节顺序

5. 字符串存储

6. 代码的二进制表示

7. 布尔代数运算

8. 逻辑运算

9. 移位运算

二、 整数表示

1. 有符号与无符号表示

1.1 表示范围

1.2 补码编码的有符号数

1.3 无符号数

2. 无符号数与有符号整数之间的转换

3. 扩展数字位数与截断数字位数

3.1 位数扩展

3.2 位数截断

三、整数运算

1. 加法

1.1 无符号数加法

1.2 有符号数加法

1.3 加法逆元（无符号数求反、有符号数求非）

2. 乘法

四、浮点数

1. 二进制表示的限制

2.IEEE表示形式

3. 舍入

3.1 实数舍入到浮点数

3.2 float与int之间的转换

4. 浮点数运算

---

主要介绍C语言中有符号整数（以补码形式表示）、无符号整数、浮点数的二进制机器代码表示，以及它们各自的算术运算（包括加减乘除与算术移位）与逻辑运算（与或非与逻辑移位）。以及整数之间转换时、舍入时、溢出时的情况。

一、信息存储：

1. 空间大小定义

字节：8位，是最小的可寻址内存地址。

字长：每台计算机的字长，指明了指针数据的标称大小，也决定了虚拟地址空间的最大值。对于w位的机器而言，最多访问2^w个字节。如32位机器可访问2^32=4,294,967,296Byte≈4G字节，即4GB。64位可访问约16EB。（使用gcc编译时，带上参数-m32可使代码能同时在64位与32位机器上运行，而-m64的代码只能在64位机器上运行。）

2. 不同进制的转换方法

一般的十进制转十六进制、二进制，用商一直除16、2，将余数倒排：

当十进制为2的非负整数n次幂时，转十六进制可以套用公式，n=i+4j，十六进制为1(i=0)、2(i=1)、4(i=2)或8（i=3）后面接j个0。如2048=2^11，n=11=3+4*2，十六进制则为800。

这种方式十六进制不可能以3、f等开头，如0xF0，二进制为11110000=2^4+2^5+2^6+2^7 =240≠2^22，240不是2的整数幂。所以如果一个数是2的幂，用16进制标识第一位只能是1/2/4/8。

3. 各种数据类型所占字节数

数据类型占的内存大小与操作系统和编译器有关，每个编译器都可以为自己的硬件自由选择合适的大小，只受以下限制：short和int至少为16位，long至少为32位，short不长于int，int不长于long。

对于当今的主流编译器，C的各种数据类型占字节数如下：

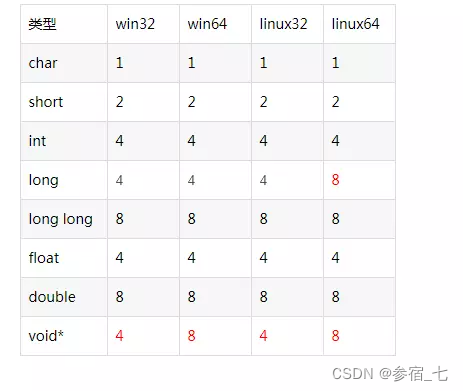
对于前面加上Unsigned关键字的类型，所占字节数不变。

布尔类型：C中没有bool类型，但是C++中有，虽然理论上bool类型只需要占1位，但因为字节是最小寻址内存地址，所以C++中的bool类型实际上和char一样占1个字节，如何在C中使用或定义bool类型，参考资料：C语言中的bool类型_热带巨兽的博客-CSDN博客_c bool类型；java中如果boolean类型是单独使用的话，编译器会将其转换为int，占4个字节，如果是以数组方式使用的话，则会将其转换为byte数组。为什么单独使用是转换成int，而不转换成byte呢？可以参考：Java中的boolean类型到底占用多少个字节？_WQ同学的博客-CSDN博客_java布尔类型占用多少字节。

本文使用Linux64的情况，即long类型与指针均占8字节。

C语言与编译器维护着数据类型，但编译器生成的机器级程序并不包含数据类型的信息。

4. 字节顺序

大端法：将表示一个数字的字节正序存储（其实是字节的高位存在内存的地址的低位）。小端法：将表示一个数字的字节逆序存储。如十六进制值0x01234567，在内存中存储的顺序如下图所示：

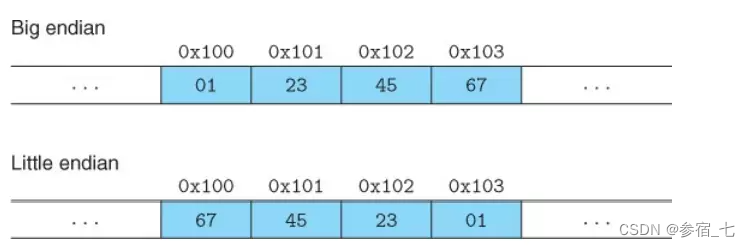
大部分机器都是使用小端法，小端法在对数据进行位数扩展与截断时不会改变改数据在内存的地址，比如将上述Int类型转为short（位数截断），如果使用小端法，short的地址还是0x100,而大端法的地址则会变为0x102。扩展同理。（参考：为什么大部分cpu要做成小端模式，一定要这么做吗？ - 知乎为什么大部分cpu要做成小端模式，一定要这么做吗？ - 知乎）

但java虚拟机与网络字节序列都是用的大端法。在网络上传输数据时，为保证所有机器能正确处理接收的数据，发送方需要在传输前将数据都转换成统一字节顺序的规则，接收时各机器再转换成自己的字节顺序。

5. 字符串存储

字符串被编码为一个以null（十六进制为00）结尾的字符数组，每个字符以标准编码来表示（一般是ASCII码），字符串不会随机器的字节顺序改变。

6. 代码的二进制表示

由于不同的机器有不同的指令集，以及对指令的二进制编码不同，所以可执行二进制文件不能跨平台运行。

7. 布尔代数运算

布尔代数包括~ & | ^，其中|对&具有分配律，就像乘法对加法具有分配率：a | (b & c)=(a | b) & (a | c)。

a^a=0，即对于^,每个数的逆元是其本身，该操作通常用于将一个寄存器清0。

一个二进制序列可以作为一个mask，如网络IP中的掩码。将mask&目标码，可以使目标码上只有指定位置有效。要生成一个形如0……01……1的mask，采用式子1<<k-1。

8. 逻辑运算

逻辑运算包括&& || ！，逻辑运算认为所有非0的参数都为true，返回1（只有字节的最后一位生效）。与布尔代数不同，对于&&或者||，如果第一个参数就能确定结果，那么就不会计算第二个参数。

9. 移位运算

1) 逻辑右移：在左边补0；算术右移：在左边补符号位，基本上所有机器和编译器都对C语言中的有符号数使用算术右移。而Java中，>>表示算术右移，>>>表示逻辑右移。

2) 左移：在右边补0。

3) 当移位的位数超过数字本身的位数时：

三个值的结果分别表示移位了0、4和8：

4) 加减法的优先级比移位运算高

二、 整数表示

1. 有符号与无符号表示

1.1 表示范围

64位程序上C语言中常见数据类型的表示范围：

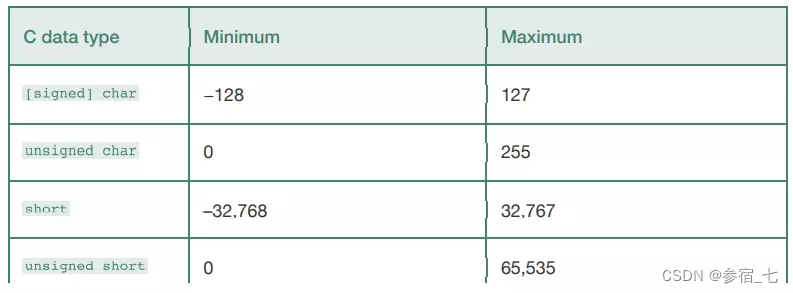
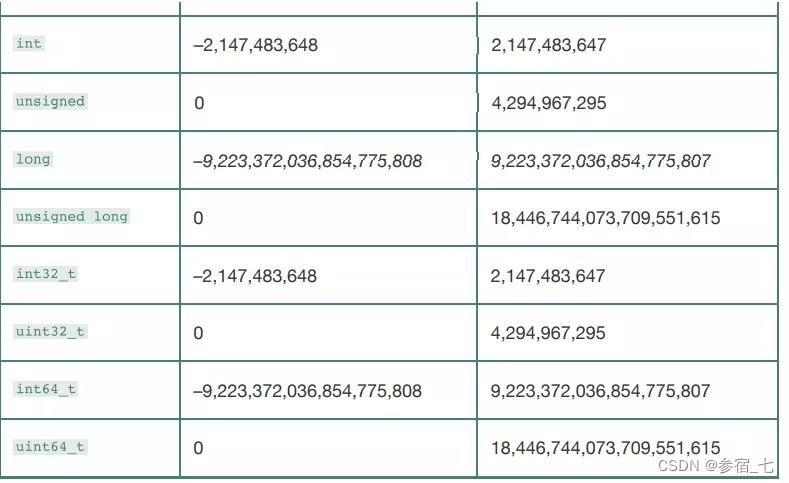
1.2 补码编码的有符号数

（1）Java中的整数与几乎所有机器上的C中的有符号数使用补码编码，其中负数比正数多一位，1000 0000表示最大负数，0111 1111表示最大正数，0000 0000表示0，1111 1111表示-1（在无符号数中为最大正数）。

（2）一个补码编码的二进制负数转为十进制：

以11011为例：1011=-1*2^4+1*2^3+0*2^2+1*2^1+1*2^0=-5

-x的补码表示可以使用2^w-x计算。如x=6时，2^3-6=2,2=10（BIN），-6=110（BIN）

（3）对于有符号数的下限，在程序中使用-2147283647-1表示，而不直接写为-2147283648，因为当编译器遇到-X时，会先确定X的类型与大小，然后再取负，但是2147283648是C不能使用int类型表示的大正数，所以会将其转换为long long 类型或者unsigned int类型后再取负。

（4）反码在现在机器中几乎不用。原码会在浮点数中使用，原码的最高位决定其他位应该取正权还是负权，如,1010=-2^1=-2，且以0000 0000表示+0,1000 0000表示-0。

（5）补码的加减法，补码的加法与十进制加法类似，该进位进位，该借位借位；而y-x，则求-x值的补码表示（求一个十进制负数的补码，可求其原码取反加一），再做加法y+(-x),高位直接舍弃。参考：补码的加减法运算_不去上课的博客-CSDN博客_补码加法

1.3 无符号数

除了C语言，很少有其他语言支持无符号数，应该少使用C语言的无符号数。除非我们将这些字节整体不看做一个数，而是看做掩码，或者多个bool值的集合等，不可能涉及数据类型转换时，可以使用无符号数。

2. 无符号数与有符号整数之间的转换

机器在执行类型转换时，位上的0与1不会因为数据类型而更改，只是改变了C编译器解释这些位的方式。

1）有符号数→无符号数：

对于负数，一个字节的有符号解释的相反数与无符号解释之和为2^w，如十六进制为0xCFC7的16位为模式即是-12345的补码表示，又是53191的无符号表示，而12345+53191=65536=2^16。即T2U(x)=2^w+x，如T2U(-3)=16+(-3)=13。

对于非负数：T2U(x)=x

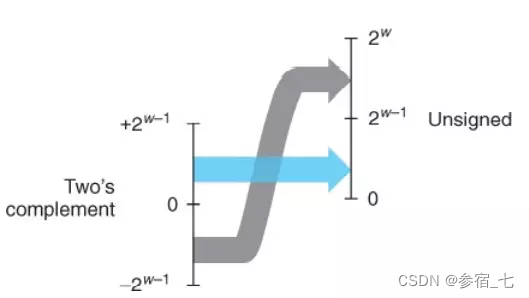
2）无符号数→有符号数：

对于x＜2^(w-1)的数，U2T(x)=x；

对于x≥2^(w-1)的数，U2T(x)=x-2^w。

3) 在C语言中，存在隐式类型转换，当有符号数与无符号数同在一个表达式中，编译器会将有符号数隐式转换为无符号数进行计算。这样的话，对于<、>、==等比较运算符来说，会出现反直觉的结果，如-1<0U，因为0U为无符号数，-1将被转换为UMAX（最大的无符号数），所以结果为false。

3. 扩展数字位数与截断数字位数

3.1 位数扩展

无符号数为左边添0扩展，有符号数为左边添符号位扩展（类似于算术右移时，左边的位变化）

注意有符号负数左边添符号位扩展不影响数值大小：1000=-2^3，1111 1000=-2^7+2^6 +2^5+2^4+2^3=-2^3。

将short转换成unsigned int时，先对位数进行扩展，在从int转换为Unsigned。

3.2 位数截断

C语言中把Int转换为short时，会对字节的前k位进行位数截断。论字节顺序是大端小端，截掉的位是一样的，但大端法会导致截断后变量在内存的地址发生改变。

对于w位的无符号数，截断前面k位，就保留后面w-k位；对于w位的有符号数，截断前面k位，可能会影响值的正负。

三、整数运算

1. 加法

对于w位的两个数的加法，有时需要w+1位才能保存结果，但是C不会为其分配w+1位，所以当需要w+1位时，C会进行位数截断。

1.1 无符号数加法

(x+y)mod(2^w)为C得到的结果，即只留下w位，舍弃溢出的w+1位。

如何判断结果是否溢出而被截断了？当溢出时，result舍去了最高位，相当于是减了2^w，那么result一定将小于x与y。

1.2 有符号数加法

当x+y正溢出时，符号位的2^(w-1)被溢出为1，解释为-2^(w-1)，一去一回相差2^w，所以结果为x+y-2^w；

当负溢出时，溢出的位置一定为1，符号位一定为0，因为11……与01……（第二个1为符号位）都相当于1……（第一个1位符号位），溢出的位被舍弃，所以结果为x+y+2^w。如-14的补码为10010，在4位补码的表示,0010，权值为-2^w的1被舍弃。

如何判断结果是否溢出而被截断，只有当x、y符号相同时，才可能溢出，当结果与x/y相反时，出现溢出。

1.3 加法逆元（无符号数求反、有符号数求非）

即-x，一个数与它的加法逆元相加为0。

无符号数的逆元-x=2^w-x，0的逆元为0。

有符号数的逆元为-x。TMIN的逆元为其本身。

任何整数的-x=~x+1(~x为按位取反，或称为补)。

2. 乘法

（1）同加法一样，无符号数乘法也是截断位数，只留下后面的w位，所以x*y=(x*y)mod (2^w)；

有符号数的乘法是先截断留下w位，再将剩下的w位翻译成补码，x*y=U2T((x*y)mod(2^w))

（2）当乘法溢出时，无符号数与有符号数如果乘数的位都相同，乘积截断前的位不同，但是截断后的位都会相同，如：

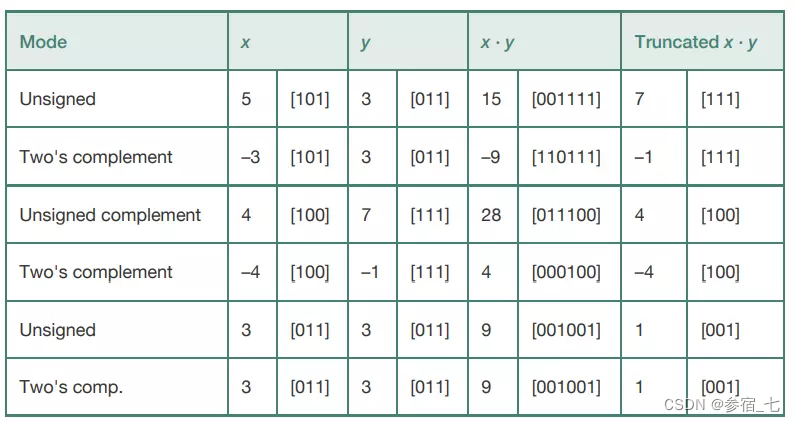
（3）因为机器在执行乘法时比较慢，所以程序中出现乘以常数时，编译器通常使用移位与加法组合来替代乘法，如3a=（a<<1）+a。

除法比乘法更慢，编译器使用右移来实现除以2的幂，不论是正还是负，结果都会向下舍入（舍去的右边的1，其权值都为正，降低了整个被除数，导致结果偏小）。

有符号整数与无符号整数的计算对比：

有符号整数由于溢出时会导致符号位被淹没，所以结果的正负可能是错的。

四、浮点数

1. 二进制表示的限制

二进制小数，其小数点前每位的权值是2^m，小数点后的权值是2^(-m）。正如不能用十进制小数准确地表示出1/3一样，二进制小数也有一些不能准确表示的值，如1/5。二进制只能准确地表示能被写为x*2^y的数，即对于范围内的部分整数也不能准确表达。在数轴上表示为小范围内均匀，大范围内越靠近0越稠密：

2.IEEE表示形式

（1）IEEE浮点表示为V=(-1)^s*M*2^E

s：符号位，为0或1；

E：阶码，可能为负数。

M：尾数，二进制小数，依赖于e是否等于0。

C语言中float类型E为8位，M为23位；double类型E为11位，M为52位。

（2）浮点数分为几种情况：

1）e既不为全1也不为全0，阶码E为二进制e-Bias，Bias=2^(k-1)-1，之所以要减bias，是为了使幂的范围覆盖正负（-126~127）。如，阶码二进制e为0000 0110，则阶码E为6-（128-1）=-121。尾数M隐含地以1开头（这样可以省一位），只表示小数部分。

整数12345的二进制为0……011000000111001，而12345.0的二进制为0100011001000000 11100100……，两者加粗部分相同，而前者多了一个1，这就是float类型隐藏的默认的1。

2）e为全0时，阶码E为1-Bias(即-126)，而尾数不隐含以1开头（这样可以保证可表达的数与第一种情况平滑相接）。此时，当s为1时表示-0.0，当s为0时，表示+0.0。

3）e为全1，当M为全0时，s为1表示负无穷，s为0表示正无穷，可以在溢出时用到。当M不为全0时，表示NaN，如根号（-1）。

3. 舍入

3.1 实数舍入到浮点数

因为程序员可能输入浮点型不可表示的数值，如0.2，这时，机器会使用最接近的浮点数来表示该值，这就是舍入。对于两个浮点可以表示值的正中间，IEEE提供了向0舍入（从浮点数转为int类型时采用）、向上舍入、向下舍入和向偶数舍入（即最后一位为0，默认使用这种，因为不会造成统计学上的偏差）。

3.2 float与int之间的转换

int→float：数字不会溢出，但会舍入（向偶舍入）。不会溢出是因为，虽然float只有23位表示精度，而int有32位表示精度，但是因为float有指数，所以整体范围更大。

float→int：会溢出与舍入（向零舍入）。

4. 浮点数运算

浮点数的加法、乘法是可交换但不可结合的，因为一些情况的结合相较于没结合，会导致中间结果的舍入（或者原来会舍入，而结合后不会舍入），从而影响最终结果，如(3.14+1e10)-1e10会导致3.14被舍入，结果为0.0；而3.14+(1e10-1e1 0)不会引起舍入,结果为3.14。

另外，浮点的乘法不对加法具有分配性，如1e20*(1e20-1e20)=0，而1e20*1e20-1e20*1e20 =NaN（相当于正无穷-正无穷）。

浮点数与整数的计算对比：

计算机整数（包括有、无符号）的算术运算与逻辑运算满足数学上该有的结合律与交换律。而浮点数不满足结合律，因为浮点数表示的精度有限，可能导致中间结果舍入（或者该舍入却没舍入）。

但因为浮点数的溢出会表示为正无穷与负无穷，所以计算结果的正负始终是对的，而有符号数溢出会导致结果符号相反。