模拟退火算法

模拟退火算法流程图

初始温度
- 新温度值
  - 进入循环
    - 生成新的解
      - 按照 bound
      - 按照 constraint
    - 计算新解与当前解的目标差异
    - 判断是否接受解
    - 判断是否更新解
  - 循环结束
- 按照温度降低率降低温度
温度小于最低温度
输出结果

模拟退火算法示例代码1

$min=x_1^2+2x_1-15+32x_2+4x_2^2$

import numpy as np

def objective_function(x):
    return x[0]**2 + 2*x[0] - 15 + 4*4*2*x[1] + 4*x[1]**2

def simulated_annealing(objective_func, initial_solution = np.array([0, 0]), \
                        temperature = 100, min_temperature = 0.1, \
                        cooling_rate = 0.90, iter_max = 100, seed = 0):

    np.random.seed(seed)
    current_solution = initial_solution
    best_solution = current_solution

    while temperature > min_temperature:
        for j in range(iter_max):
            # 生成新的解
            new_solution = current_solution + np.random.uniform(-1, 1, len(current_solution))
            
            # 计算新解与当前解之间的目标函数值差异
            current_cost = objective_func(current_solution)
            new_cost = objective_func(new_solution)
            cost_diff = new_cost - current_cost
            
            # 判断是否接受新解
            if cost_diff < 0 or np.exp(-cost_diff / temperature) > np.random.random():
                current_solution = new_solution
            
            # 更新最优解
            if objective_func(current_solution) < objective_func(best_solution):
                best_solution = current_solution
        
        # 降低温度
        temperature *= cooling_rate
    
    return best_solution


# 调用退火算法求解最小值
best_solution = simulated_annealing(objective_function)

print(f"函数最小值： {objective_function(best_solution)} 自变量取值：{best_solution}")

运行结果

模拟退火算法示例代码2

$\begin{matrix} min=a_1((x_2^2-x_1^2)/3-a_1-a_2)+(a_2+a_3)(a_3+(x_1^2+x_2^2+x_2^3)/3)-(a_1+a_3)(a_3*x_1*x_2) \\ cons:5<a_1+a_2+a_3<10 \end{matrix}$

import numpy as np

global x_bound 
global x_up 

x_bound = 3
x_up = 10

def fun1(p0, p1):
    return (x_up**2 - x_bound**2)/3 - p0 - p1 

def fun2(p2):
    return p2 + (x_up**2 + x_bound**2 + x_bound**3)/3

def fun3(p2):
    return (x_up**2 * x_bound**2)*p2
   
def cons(try_solution):
    return 5 < np.sum(try_solution) < 10
    
def objective_function(params):
    return params[0]*fun1(params[0], params[1]) + fun2(params[2])*(params[1] + params[2]) - fun3(params[2])*(params[0] + params[2])


def simulated_annealing(objective_func, initial_solution = np.array([0, 0, 9]), \
                        temperature = 100, min_temperature = 0.1, \
                        cooling_rate = 0.90, iter_max = 100, seed = 0):

    np.random.seed(seed)
    current_solution = initial_solution
    best_solution = current_solution

    while temperature > min_temperature:
        for j in range(iter_max):
            # 生成新的解
            FLAG = True
            
            for k in range(iter_max):
                try_solution = current_solution + np.random.uniform(-1, 1, len(current_solution))
                if cons(try_solution):
                    new_solution = try_solution
                    FLAG = False
                    break
            if FLAG:
                print(f"找不到满足约束的解 在温度{temperature}")
                break
            
            # 计算新解与当前解之间的目标函数值差异
            current_cost = objective_func(current_solution)
            new_cost = objective_func(new_solution)
            cost_diff = new_cost - current_cost
            
            # 判断是否接受新解
            if cost_diff < 0 or np.exp(-cost_diff / temperature) > np.random.random():
                current_solution = new_solution
            
            # 更新最优解
            if objective_func(current_solution) < objective_func(best_solution):
                best_solution = current_solution
        
        # 降低温度
        temperature *= cooling_rate
    
    return best_solution


# 调用退火算法求解最小值
best_solution = simulated_annealing(objective_function)

print(f"函数最小值： {objective_function(best_solution)} 自变量取值：{best_solution}")

模拟退火算法的可视化

import numpy as np
import matplotlib.pyplot as plt

global x_bound
global x_up

x_bound = 3
x_up = 10

def fun1(p0, p1):
return (x_up**2 - x_bound**2)/3 - p0 - p1

def fun2(p0, p1):
return p1 + (p0**2 + x_bound**(p1-p0))/3

def cons(try_solution):
return 5 < np.sum(try_solution) < 10

def objective_function(params):
return params[0]*fun1(params[0], params[1]) + (params[0] + params[1])*fun2(params[0], params[1])

def simulated_annealing(objective_func, initial_solution = np.array([4, 4]), \
temperature = 100, min_temperature = 0.1, \
cooling_rate = 0.90, iter_max = 100, seed = 0):

np.random.seed(seed)
current_solution = initial_solution
best_solution = current_solution
RECODE_temp,RECODE_sol = [],[]
raw_temperature = temperature

while temperature > min_temperature:
RECODE_temp.append(temperature)
for j in range(iter_max):
# 生成新的解
FLAG = True

for k in range(iter_max):
try_solution = current_solution + np.random.uniform(-1, 1, len(current_solution))
if cons(try_solution):
new_solution = try_solution
FLAG = False
break
if FLAG:
print(f"找不到满足约束的解在温度{temperature}")
break

# 计算新解与当前解之间的目标函数值差异
current_cost = objective_func(current_solution)
new_cost = objective_func(new_solution)
cost_diff = new_cost - current_cost

# 判断是否接受新解
if cost_diff < 0 or np.exp(-cost_diff / temperature) > np.random.random():
current_solution = new_solution

# 更新最优解
if objective_func(current_solution) < objective_func(best_solution):
best_solution = current_solution

# 降低温度
temperature *= cooling_rate
RECODE_sol.append(best_solution)

RECODE_temp = [raw_temperature - i for i in RECODE_temp]
RECODE_sol = [objective_function(i) for i in RECODE_sol]
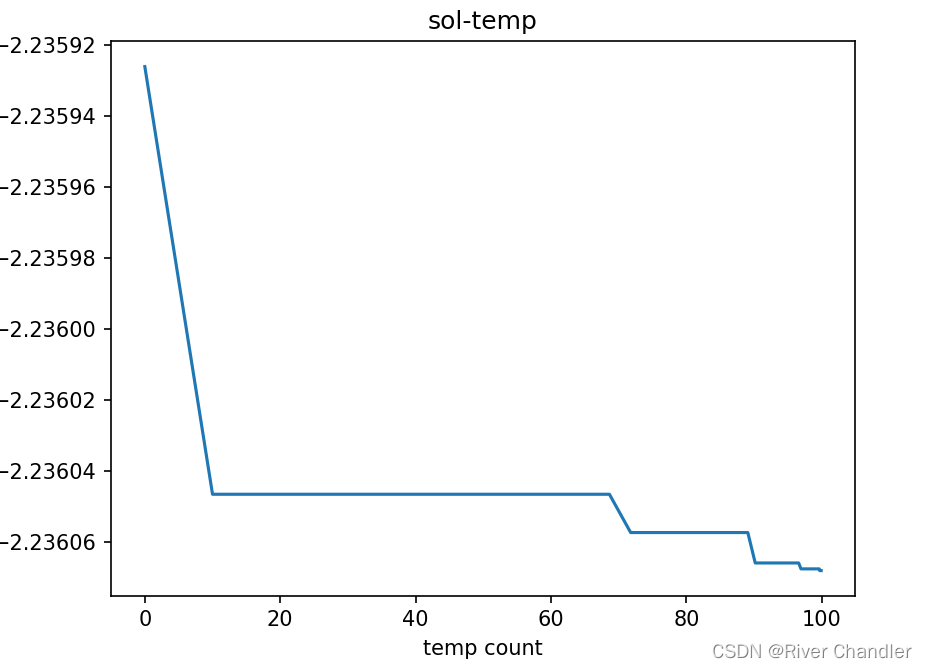
plt.plot(RECODE_temp, RECODE_sol)
plt.title("sol-temp")
plt.xlabel("temp count")
plt.ylabel("sol")
plt.pause(0.01)
return best_solution

# 调用退火算法求解最小值
best_solution = simulated_annealing(objective_function)

print(f"函数最小值： {objective_function(best_solution)} 自变量取值：{best_solution}")

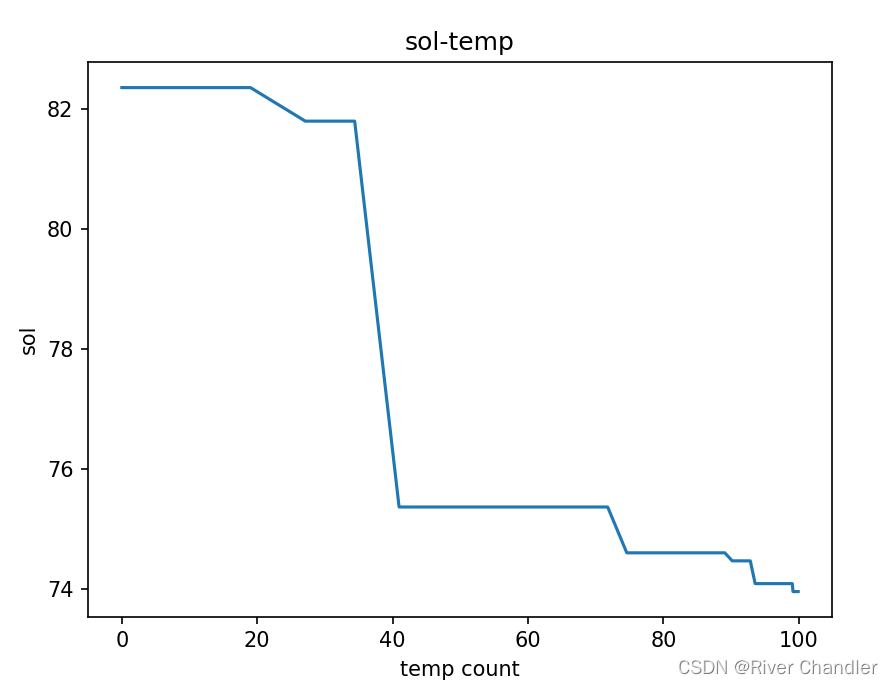
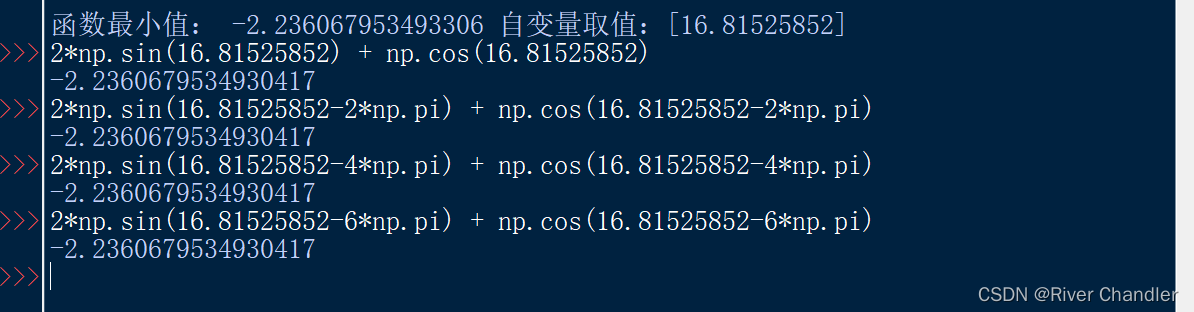
example 2sin(x)+cos(x)

import numpy as np
import matplotlib.pyplot as plt

def objective_function(params):
    return 2*np.sin(params[0]) + np.cos(params[0])

def cons(try_solution):
    return True

def simulated_annealing(objective_func, initial_solution = np.array([4, ]), \
                        temperature = 100, min_temperature = 0.1, \
                        cooling_rate = 0.90, iter_max = 100, seed = 0):

    np.random.seed(seed)
    current_solution = initial_solution
    best_solution = current_solution
    RECODE_temp,RECODE_sol = [],[]
    raw_temperature = temperature
    
    while temperature > min_temperature:
        RECODE_temp.append(temperature)
        for j in range(iter_max):
            # 生成新的解
            FLAG = True
            
            for k in range(iter_max):
                try_solution = current_solution + np.random.uniform(-1, 1, len(current_solution))
                if cons(try_solution):
                    new_solution = try_solution
                    FLAG = False
                    break
            if FLAG:
                print(f"找不到满足约束的解 在温度{temperature}")
                break
            
            # 计算新解与当前解之间的目标函数值差异
            current_cost = objective_func(current_solution)
            new_cost = objective_func(new_solution)
            cost_diff = new_cost - current_cost
            
            # 判断是否接受新解
            if cost_diff < 0 or np.exp(-cost_diff / temperature) > np.random.random():
                current_solution = new_solution
            
            # 更新最优解
            if objective_func(current_solution) < objective_func(best_solution):
                best_solution = current_solution
        
        # 降低温度
        temperature *= cooling_rate
        RECODE_sol.append(best_solution)

    RECODE_temp = [raw_temperature - i for i in RECODE_temp]
    RECODE_sol = [objective_function(i) for i in RECODE_sol] 
    plt.plot(RECODE_temp, RECODE_sol)
    plt.title("sol-temp")
    plt.xlabel("temp count")
    plt.ylabel("sol")
    plt.pause(0.01)
    return best_solution


# 调用退火算法求解最小值
best_solution = simulated_annealing(objective_function)

print(f"函数最小值： {objective_function(best_solution)} 自变量取值：{best_solution}")