---

【可更换其他算法，获取资源请见文章第6节：资源获取】

---

1. 蜣螂优化算法DBO

蜣螂优化算法可参考DBO介绍

2. 变分模态分解VMD

变分模态分解（Variational Mode Decomposition，简称VMD）是一种信号分解和降噪方法，用于从复杂的信号中提取出不同的成分或模态。

VMD是在2014年由Konstantin Dragomiretskiy和Dominique Zosso提出的。它基于变分原理，通过最小化信号的复杂度和不同成分之间的相互影响，将信号分解成多个固有模态（Intrinsic Mode Functions，简称IMFs）。IMFs是具有不同频率和振幅的函数，相当于将原始信号分解成一系列振动模态。

VMD适用于处理非线性和非平稳信号，例如振动信号、生物信号、地震信号、图像信号等。它在信号处理、振动分析、图像处理等领域有广泛的应用，特别是在提取信号中的隐含信息和去除噪声方面表现出色。

各个功率模态分量$u_k$的频谱通过希尔伯特转换被传送至基带，并将其与一个指标对应的估计中心频率$w_k$相对应，最终通过解调信号高斯平滑度来估算该带宽，从而将该约束的变分问题表达为：

式中，$u_k$代表第$k$个功率模态分量；$w_k$代表功率模态分量的中心频率；$\delta (t)$代表单位冲击函数。同时，采用二次惩罚算子及拉格朗日乘子达到排除以上因素的限制的目的，将上面式子的最小化问题转变为下面式子的无约束优化问题。

式中，$\alpha$代表惩罚算子，在时间序列信号中混有噪声可保证其重构后的精度；$\lambda$代表拉格朗日的乘子；$\otimes$表示卷积算子。

随后更新功率模态分量$u_k$，即：

式中，$i$和$n$都是代表不同参数取得的任意值；$\omega$表示信号从时间域向$t$频率域变换的符号；$\hat{u}$、$\hat{f}(\omega )$和$\hat{\lambda }(\omega )$是傅里叶变换后的$u$、$f(\omega )$和$\lambda (\omega )$。

最终，以上面式子同样的方式更新${\omega }_k^{n+1}$与${\lambda }_k^{n+1}$即可。

当满足特定的判别精度$\delta$后，终止循环迭代。

式中，$\epsilon$表示收敛进度。最终，将原功率序列分解为$k$个窄频段IMF。

3. 核极限学习机KELM

KELM模型是在 ELM 的基础上延伸建立的，ELM 模型中的随机映射被替换成了核映射，通过把低维问题转换到完整的内积空间里解决，可以极大地减少网络的复杂性，与 ELM 相比具备更强的学习泛化能力和稳定性。

ELM算法采用随机生成各个神经元连接权值和阈值，这会导致算法的波动和不稳定，所以在ELM 算法中当映射函数$h(x)$为未知时，引入了核函数，KELM 的数学描述如下：

式中，$H$表示隐含层输出矩阵；$K(x_i,x_j)$表示核函数，本文采用RBF核函数，即：

式中，$g$为核参数。可以得到KELM的输出函数表达式为：

式中，$\beta$为输出权值矩阵；$T$为目标输出矩阵；$I$为单位矩阵；$C$为正则化系数。

综上，KELM的核参数$g$和正则化系数$C$是影响预测性能的重要因素，这也正是本文所使用的优化算法需要优化的两个参数。

4. 部分代码展示

%%  蜣螂算法参数设置
% 优化参数的个数dim为2 。
%  目标函数
fun = @getObjValue; 

dim = 2;
% 优化参数的取值上下限（正则化系数C 核函数参数矩阵g ）
lb = [25 2];
ub = [60 5];

%%  参数设置
pop =20; %种群数量
Max_iteration=100;%最大迭代次数             
%% 优化(调用函数)
[Best_pos,Best_score,Convergence_curve]=DBO(pop,Max_iteration,lb,ub,dim,fun);

x=Best_pos  ;                %最优个体 
C = x(1);                    %正则化系数
Kernel_type = 'RBF';         %核函数名
Kernel_para = x(2);          %核函数参数矩阵

output_train=shuchu(nn(1:geshu),:);
output_test=shuchu(nn((geshu+1):end),:);

figure
plot(output_train )
hold on
plot(train_simu1  )
legend('真实值','预测值')
title('训练集')

figure
plot(output_test )
hold on
plot(test_simu1 )
legend('真实值','预测值')
title('测试集')

figure
plot(Convergence_curve)
title('适应度曲线')
xlabel('迭代次数')
ylabel('适应度')
%%
reay = output_train;   % 真实数据
prey = train_simu1 ;   % 仿真数据
reay = reshape(reay,1,size(reay,1)*size(reay,2));   % 真实数据
prey = reshape(prey,1,size(prey,1)*size(prey,2));   % 仿真数据
num=length(reay);%统计样本总数
error=prey-reay;  %计算误差
mae=sum(abs(error))/num; %计算平均绝对误差
me=sum((error))/num; %计算平均绝对误差
mse=sum(error.*error)/num;  %计算均方误差
rmse=sqrt(mse);     %计算均方误差根
r=min(min(corrcoef(prey,reay)));
R2=r*r;

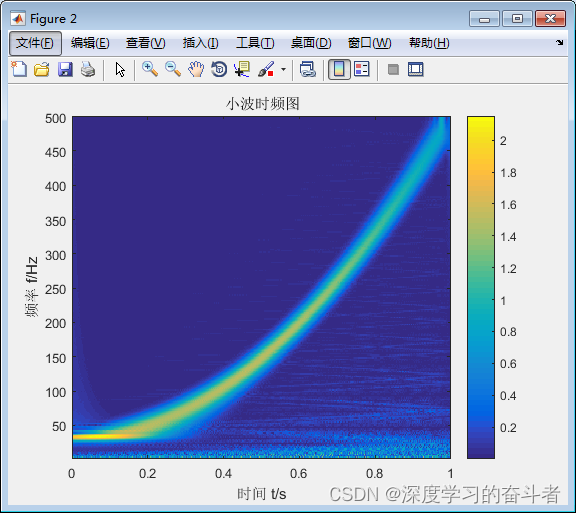
5. 仿真结果展示

6. 资源获取

可以获取完整代码资源，可更换其他群智能算法。