AGC028

Removing Blocks

High Elements

好仙啊。

我会转化！！问题转化为在原序列剩下的数中取$IS$序列$a$,$b$，满足$cx+|a|=cy+|b|$ 。对于没在$a,b$序列中的数，可以通过恰当放置使其不对前缀最大值的集合造成影响。

我会分析性质！！对于原序列的前缀最大值一定会在$a$,$b$之中。

我会调整！！将$a$,$b$同时删去一个不是前缀最大值的数，$a$,$b$其中之一只会由前缀最大值组成。

应该会做了吧

Jigsaw

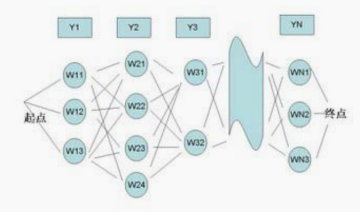
问题转化为，对于一个弱连通图

拆分成若干条起点$\le H$，终点$>H$的链，每条边恰好经过一次

考虑合法的条件：

$1.1$ 对于任意$\le H$的点，入度$\ge$ 出度
$1.2$ 对于任意$>H$的点，入度$\le$ 出度
$1.3$存在一个点的入度$\ne$出度

证明：考虑构造超级源汇点，得到从超级源点出发的欧拉回路，每次回到超级源点就得到了一条合法路径，这些路径包含了所有边。

AGC007

Shik and Copying String

把每个字符的转移路径画下来发现是若干条折线

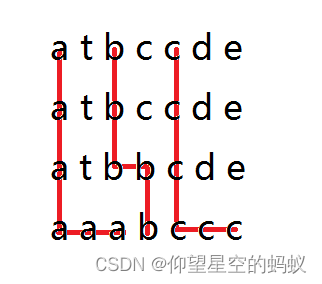
合法的方案应该满足：

$1.1$折线之间两两不相交
$1.2$折线只能向下或向右延伸

显然我们可以按$t$串从后往前贪心，观察到每次新增一条折线，原来的拐点都会向左下挪一位，并且可能会新增一个第一层的拐点，然后把不合法的拐点弹出。答案是所有拐点的最大层数$+1$。

复杂度$O(n)$。

Pushing Balls

神仙题。

问题转化为$n$次操作，每次操作两个相邻点，贡献为两个点的距离，然后把这两个点删掉，问$n$次操作期望和。

考虑对每次操作的贡献单独计算。注意到每次操作后期望仍然是等差数列，推导如下：

记$d_j[i]$表示还剩$j$个球时第$i$个位置和第$i+1$个位置距离的期望

显然$d_j[i]=\frac{i}{2(j+1)}{d}_{j+1}[i+2]+\frac{1}{2(j+1)}(d_{j+1}[i]+d_{j+1}[i+1]+d_{j+1}[i+2])+\frac{2(j+1)-i-1}{2(j+1)}{d}_{j+1}[i]$

那么$d_j[i]=\frac{j+2}{j+1}{d}_{j+1}[i]+\frac{2i+3}{2j+2}\times D$

对于等差数列任选一个数的期望就是其中位数。复杂度$O(n)$。

Construct Sequences

首先把$a_i+b_i$的值定下来，然后从前往后构造即可。

Shik and Game

线性$dp$ + 前缀和优化。

Shik and Travel