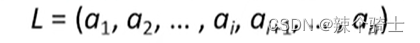第六期：树与图的遍历 🔥 🔥 🔥

蓝桥杯热门考点模板总结来啦✨ ~

你绝绝绝绝绝绝对不能错过的常考树与图的遍历模板 💥

❗️ ❗️ ❗️

大家好我是寸铁 💪

祝大家4月8号蓝桥杯上岸 ☀️

还没背熟模板的伙伴们背起来 💪 💪 💪

祝大家4月8号蓝桥杯上岸 ☀️

不清楚蓝桥杯考什么的点点下方👇

考点秘籍

想背纯享模版的伙伴们点点下方👇

想背注释模版的伙伴们点点下方👇

往期精彩回顾

想看JavaB组填空题的伙伴们点点下方 👇

竞赛干货

树与图的遍历与DFS/BFS是蓝桥杯的热门考点,距离省赛仅剩4天,干就完事了 ❗️

下面让我们开始刷起来 ❗️ ❗️ ❗️

DFS你的大脑，BFS你的体力 💪 💪 💪

让我们一起上岸蓝桥杯 ✌️

树与图的深度优先遍历🌲

树的重心

邻接表

邻接表（Adjacency List）顾名思义，就是通过链表或者利用数组模拟链表的方式将图的相连接关系表示的一种方法，存储方法跟树的孩子链表示法相类似，是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点，则把相邻顶点依次存放于表头结点所指向的单向链表中。

分析

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。
树的重心：运用DFS+邻接表
DFS:递归处理根节点的子树的节点个数
邻接表：找到节点的邻接点，继续递归，走到叶子节点时，再往上返回，直至回到根节点，再以当前根节点的邻接点作为根节点，再DFS,确保每一个点都会走到。

问题分析：

根据重心的定义：
(1)如果将这个点删除后，剩余各个连通块中点数的最大值。
我们需要遍历各个根节点，将根节点的最大子树保存下来。
(2)剩余各个连通块中点数的最大值最小。
再将各个根节点的最大子树进行比较，得出最小值，即是重心，即为答案。

模拟

以u=1作为根节点，一条路走到黑，走到叶子节点，最后返回到根节点1。
在这里插入图片描述

由于从1开始，无法体现下面与上面部分的比较
走完u=1，接下来走到u=2，以u=2为根节点。在这里插入图片描述

注：可以看到从根节点出发，递归其根节点的邻接节点，邻接节点继续递归他的邻接节点，他的邻接节点继续递归他的邻接节点，直至往下走到叶子节点，即往下再无路可走时，往上返回，直至回到根节点。
在这过程中，记录根节点的邻接节点的最大子树。再将一路走过的点进行求和，便于求解根节点的上面连通块部分。再以根节点的邻接点为根节点出发，继续往下dfs，如此循环往复，走便所有的点为止。

代码

import java.util.*;
public class Main{
    static int N=100010,M=N*2,idx,n;//输入的数是点数的两倍
    static int h[]=new int[N];
    
    static int e[]=new int[M];//最多有2倍
    static int ne[]=new int[M];//最多有2倍
    static boolean st[]=new boolean[N];//标记哪个点已走过
    static int ans=N;//先定义一个比较大的数，用于比较最小值。
    public static void add(int a,int b){//单链表存边
        e[idx]=b;//存值
        ne[idx]=h[a];
        h[a]=idx;//存边，h[a]表示的是边的编号，也是对应插入点的编号。
        idx++;
    }
    public static int dfs(int u){
        int sum=1;//本身算作一个点，用于求某个连通块的节点总数
        int res=0;//结果
        st[u]=true;//表示该节点走过，保证往下搜，防止再向上查找一遍，造成死循环。
        for(int i=h[u];i!=-1;i=ne[i]){//遍历邻接表的边
        int j = e[i];//找到节点的邻接节点。
        if(!st[j]){//如果没有走过，就dfs该节点，继续递归下去，直至走到叶子节点。
            int s = dfs(j);//让该邻接节点作为根节点，dfs该节点，统计他子树的子节点个数。
            res=Math.max(res,s);//保留的是该节点的最大子树
            sum+=s;//将该节点的各子树的节点数都加起来，便于求上面连通块的节点数。
        }
        }
        res=Math.max(res,n-sum);//比较上面连通块和下面连通块的节点数，看哪个部分比较大
        ans=Math.min(res,ans);//保存各根节点的最大子树的最小值，即删除重心，也就是答案
        return sum;//返回sum，递归处理走到的点。
    }
    public static void main(String []args){
        Scanner in = new Scanner(System.in);
         n = in.nextInt();                          
        for(int i=1;i<N;i++){
            h[i]=-1;初始化，链表开始是均指向-1
        }
        for(int i=0;i<n-1;i++){
        int a= in.nextInt();
        int b =in.nextInt();
        //无向边
        add(a,b);//a-->b
        add(b,a);//b-->a
        }
        dfs(1);
        //从1开始dfs，理论上任意一个点都可以，保险起见，防止输入的点只有一个1的情况
        System.out.println(ans);
}
}

树与图的广度优先遍历🌲

分析

题目描述

在这里插入图片描述

这里的重边和自环其实可以不用太纠结，无论是重边还是自环，只要确保两个点之间有连边，便可以进行bfs搜索，继而找到1 -> n的最短距离。
这道题是求最短距离，像最短步数、最少操作且权重为1的问题均可以用Bfs+邻接表的方式来处理。

做法

**邻接表：**存边，便于bfs搜索邻接节点。
**BFS:**一层一层往外搜，搜到一个就入队一个，再依次出队去搜索队头的邻接节点，直到搜到第n号点。如第一层搜到的为距离为1的点，第二层搜到的为距离为2的点，依次类推。
通过一层一层的bfs搜索，搜到当前节点的邻接节点，将该邻接节点入队，距离值更新为前面入队的点的距离加上1，然后邻接节点出队，又继续去搜它的邻接节点，继续一层一层往下搜，直到搜到n号点。

模拟

在这里插入图片描述
注：先从根节点开始，找到根节点的邻接节点，入队，记得更新距离。出队，再继续寻找邻接节点的邻接节点，又入队，同时，不忘更新距离。一层一层往下搜，直至第n个点。

题目模拟

在这里插入图片描述

注：
根节点从1开始，此时距离为0。然后，可以找到1的两个邻接节点，分别为2、4。并让2、4入队，更新到这两个点的距离为2。应题目要求，这里已经找到d[4]，所以直接返回答案即可。那再把队头2弹出，可以找到2的邻接节点3，更新距离为2。将3入队，此时队列还剩3、4，队头为4，再将4出队，4的邻接节点也是3，但是3已经走过，所以就不会再走。最后，队列还剩3，出队，3无邻接节点，无路可走，循环结束。

邻接表模拟

在这里插入图片描述

注：从图中可以看出新插入的节点对应建好的边的编号，通过遍历边实现遍历点。

代码

//进队、出队-->每一层能搜到的距离都是相同的
import java.util.*;
public class Main{
    static int N=100010,idx,n,m,hh,tt;
    static int q[]=new int [N];
    static int ne[]=new int[N];
    static int e[]=new int [N];
    static int d[]=new int[N];
    static int h[]=new int[N];
    public static void add(int a,int b){//邻接表
        e[idx]=b;
        ne[idx]=h[a];
        h[a]=idx;
        idx++;
    }
    public static int bfs(){
        hh=0;
        tt=0;
        q[0]=1;//队列的队头最初为1
        for(int i=1;i<d.length;i++){
            d[i]=-1;//将每个点的初始值赋为-1，表示这个点没走过。
        }
        d[1]=0;//将1赋为0，表示这个点走过。
       
        while(hh<=tt){
             int t=q[hh++];//队头元素出队
            for(int i=h[t];i!=-1;i=ne[i]){
                int j=e[i];//找到邻节点(邻边)
                if(d[j]==-1){//这个点还没走过
                d[j]=d[t]+1;//记录前一个邻接点走过的距离+当前这个点本身
                q[++tt]=j;//满足条件的入队
            }
        }
    }
    return d[n];//返回到n的距离
}
public static void main(String []args){
    Scanner in = new Scanner(System.in);
    n=in.nextInt();
    m=in.nextInt();
    for(int i =1;i<N;i++)
    {
        h[i]=-1;//初始化，指向空
    }
    for(int i=0;i< m;i++){
        int a=in.nextInt();
        int b=in.nextInt();
        add(a,b);
    }
    System.out.println(bfs());
}
}

java容器类:Queue

import java.util.*;
public class Main{
    static int N=100010;
    static int e[]=new int[N];
    static int ne[]=new int[N];
    static int d[]=new int[N];
    static int q[]=new int[N];
    static int h[]=new int[N];
    static int idx,n,m,hh,tt;
    public static void add(int a,int b){
        e[idx]=b;
        ne[idx]=h[a];
        h[a]=idx;
        idx++;   
        
    }
    public static int bfs(){
        Queue<Integer>q=new LinkedList<Integer>();
        q.add(1);
        d[1]=0;
        while(!q.isEmpty()){
            int t=q.poll();
        for(int i=h[t];i!=-1;i=ne[i]){
            int j=e[i];
            if(d[j]==-1){
                d[j]=d[t]+1;
                q.add(j);
            }
        }
    }
    return d[n];
    }
    public static void main(String []args){
        Scanner sc=new Scanner(System.in);
         n=sc.nextInt();
         m=sc.nextInt();
        Arrays.fill(h,-1);
        Arrays.fill(d,-1);
        for(int i=0;i<m;i++){
            int a=sc.nextInt();
            int b=sc.nextInt();
            add(a,b);
        }
        System.out.println(bfs());
    }
}