总结
Electra模型在使用较少的计算资源的情况下能够达到跟大语言模型相近的效果。但BART模型对于传统的BERT中加入了不同种制造noise的方式,是BERT和GPT的结合体。Electra模型主要是Generator模型和Discriminator模型的结合体。
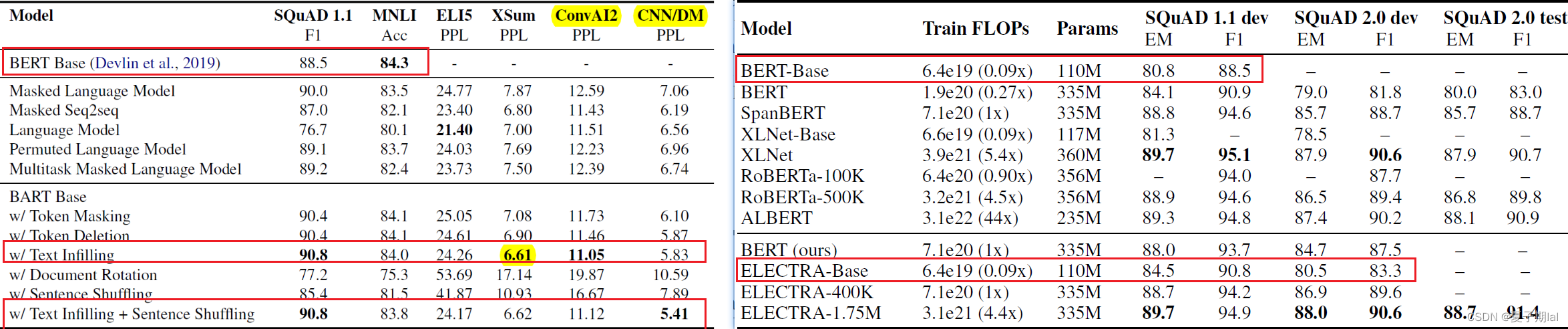
未知参数设置,两个模型在SQuAD(问答QA) 任务上的对比
网络上目前没有找到其他人有关掩码预测任务(MLM)或者(QA)任务的模型对比文件,只能根据原论文其中的实验结果简单对比。具体对比如下所示。个人觉得没有什么对比意义,需要复现相关实验,在实验中设置相同的参数相同的任务去计算相同指标进行对比。
BART模型
BART模型主要是结合了BERT的双向编码器(bidirectional encoder)和GPT的自左而右的decoder的特点。在seq2seq的transformers的模型基础上,结合了上下文语境的问题。能应用于生成任务和文本理解任务。详细图示如图所示。
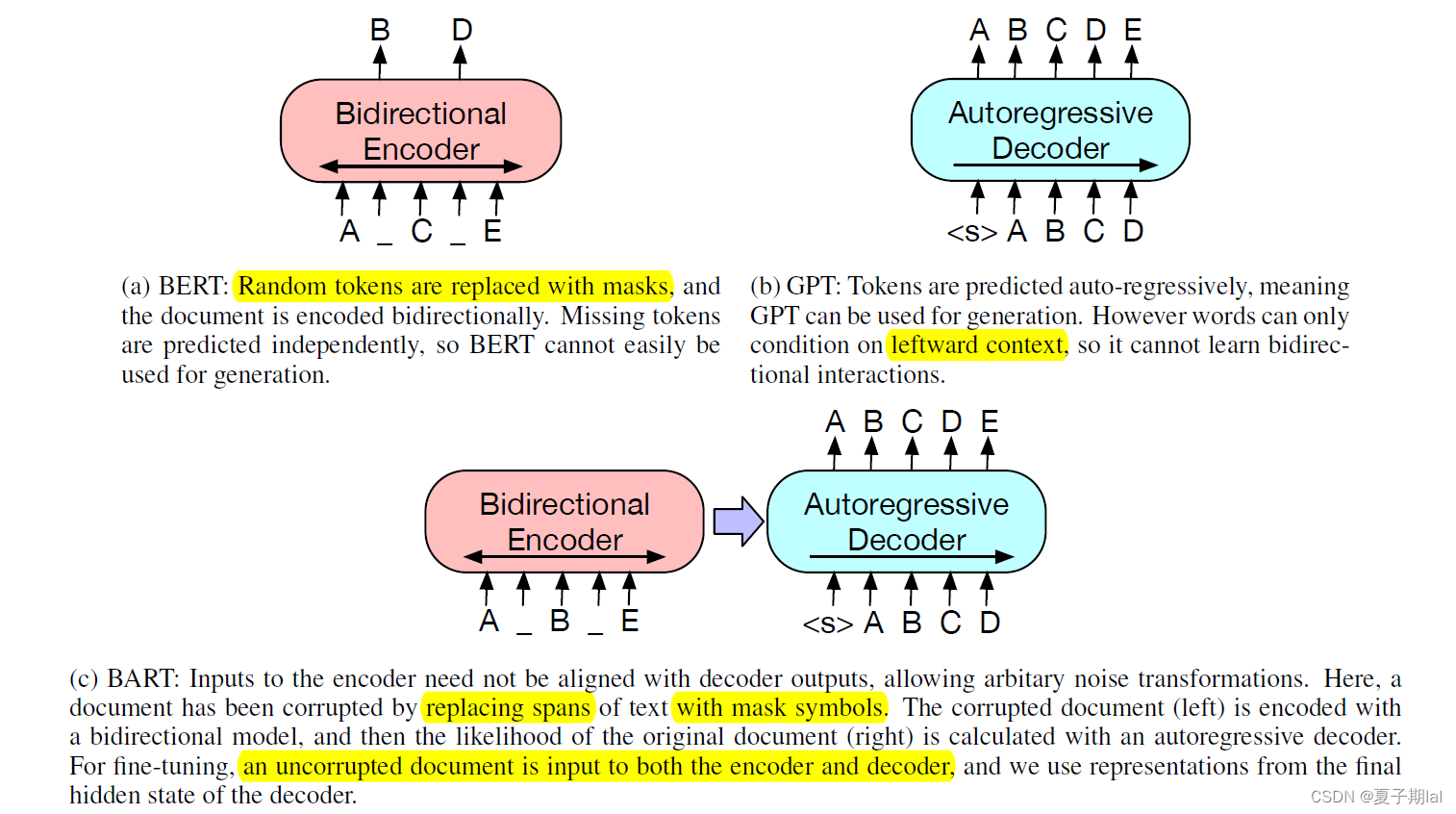
BART模型跟GPT和BERT的联系不同
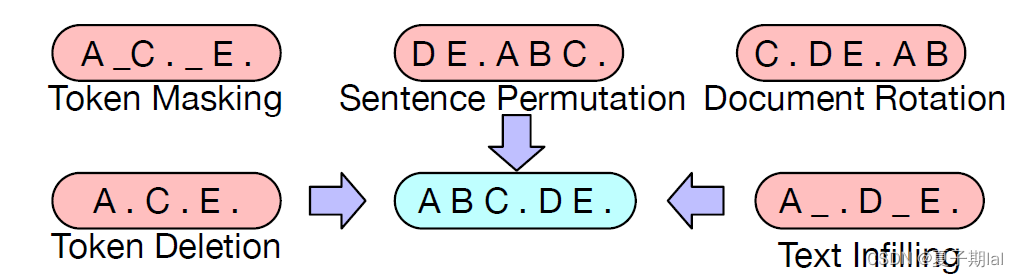
BART源自于BERT和GPT模型,结合了两个模型的优点,但对于传统的BERT的单一noise——随机用[MASK]token去掩盖单词。BART在encoder中结合了多个生成noise的方式。具体如下。
- Token masking , 随机将一个token替换为[MASK]【训练推断单个token的能力】
- Token deletion, 随机删除某些token【训练推断单个token内容以及位置的能力】
- Text infilling, 将一段连续的token【span】(1~num)替换为一个[MASK],长度服从 λ = 3 \lambda=3 λ=3的泊松分布【训练推理一段内容有多少个token的能力】
- Sentence Permuation, 将一段句子的顺序打乱(最终输出原句子)【训练推理前后句关系的能力】
- Document Rotation, 将序列中随机选取一个token,让这个token成为document的开头【提高找到document开头的能力】
具体的noise的表现形式如下图所示。(蓝色为正确文本,红色为不同破坏输入的方式)
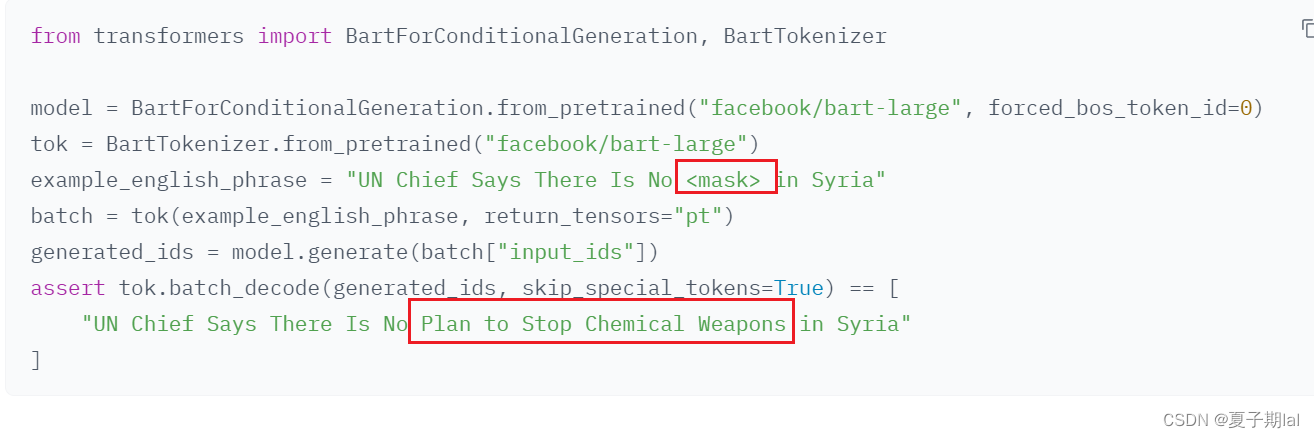
BARTmask-fill模型具体调用过程
BART在掩码预测任务中仍然使用BartForConditionalGeneration模型。在huggingface所提及的mask-filling有所提及。下图为transformers==4.31的版本的介绍。
在原论文中,主要涉及的都是问答,生成释义等任务。但并未太多提及掩码预测,但在文中处处都用了掩码预测。个人认为掩码预测是上游任务。具体的模型在下游任务的效果如下所示。
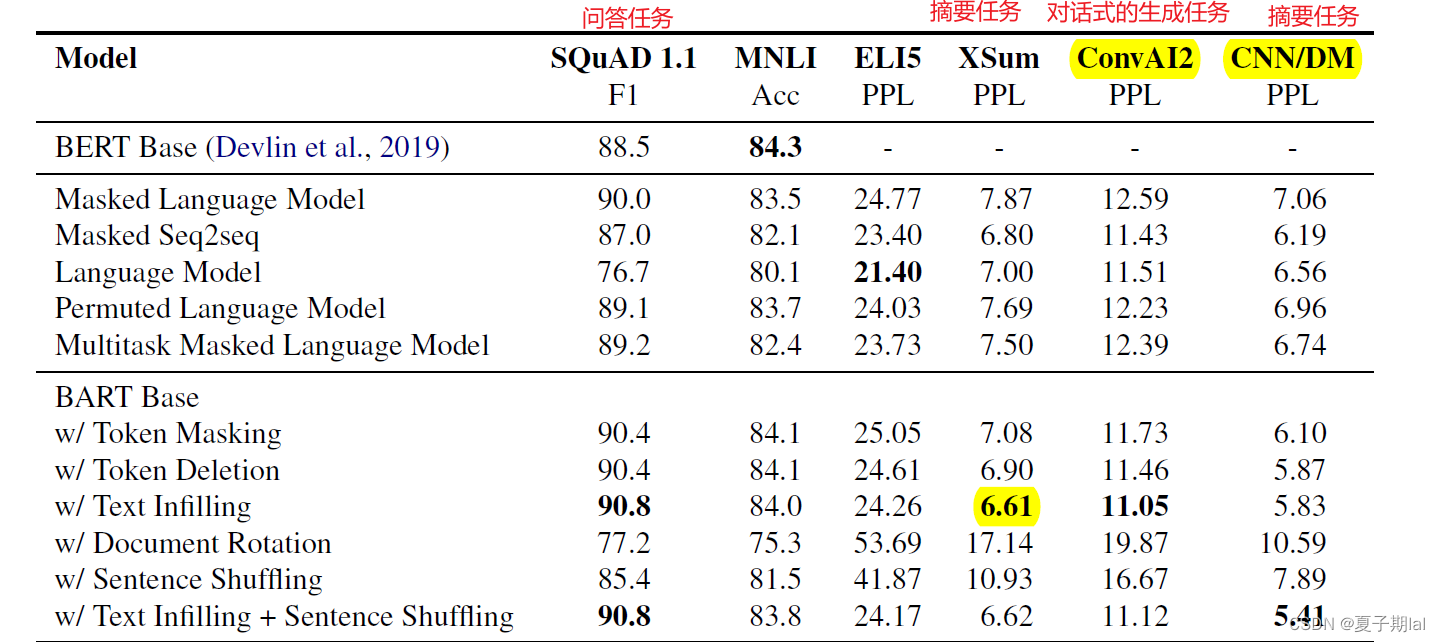
Electra模型
主要是利用了GAN对抗生成网络的思想,通过训练两种transformer模型,判别器(Discriminator)和生成器(Generator),作用分别是确定预测某些掩码[MASK]序列的token和确定序列中哪些token是否被替换。具体样例如下图所示。
因为Generator的任务是MLM模型,所以最后生成的词汇是离散的,所以梯度不能够再次传递。
在损失函数部分,因为MLM的loss明显会比判别器的loss大,所以实验通过设置参数
λ
\lambda
λ平衡。
损失函数如下图所示。
L
M
L
M
(
x
,
θ
G
)
=
E
(
∑
i
∈
m
−
log
p
G
(
x
i
∣
x
masked
)
)
\mathcal{L}_{\mathrm{MLM}}\left(\boldsymbol{x}, \theta_G\right)=\mathbb{E}\left(\sum_{i \in \boldsymbol{m}}-\log p_G\left(x_i \mid \boldsymbol{x}^{\text {masked }}\right)\right)
LMLM(x,θG)=E(i∈m∑−logpG(xi∣xmasked ))
L
Disc
(
x
,
θ
D
)
=
E
(
∑
t
=
1
n
−
1
(
x
t
corrupt
=
x
t
)
log
D
(
x
corrupt
,
t
)
−
1
(
x
t
corrupt
≠
x
t
)
log
(
1
−
D
(
x
corrupt
,
t
)
)
)
\mathcal{L}_{\text {Disc }}\left(\boldsymbol{x}, \theta_D\right)=\mathbb{E}\left(\sum_{t=1}^n-\mathbb{1}\left(x_t^{\text {corrupt }}=x_t\right) \log D\left(\boldsymbol{x}^{\text {corrupt }}, t\right)-\mathbb{1}\left(x_t^{\text {corrupt }} \neq x_t\right) \log \left(1-D\left(\boldsymbol{x}^{\text {corrupt }}, t\right)\right)\right)
LDisc (x,θD)=E(t=1∑n−1(xtcorrupt =xt)logD(xcorrupt ,t)−1(xtcorrupt =xt)log(1−D(xcorrupt ,t)))
min
θ
G
,
θ
D
∑
x
∈
X
L
M
L
M
(
x
,
θ
G
)
+
λ
L
Disc
(
x
,
θ
D
)
\min _{\theta_G, \theta_D} \sum_{\boldsymbol{x} \in \mathcal{X}} \mathcal{L}_{\mathrm{MLM}}\left(\boldsymbol{x}, \theta_G\right)+\lambda \mathcal{L}_{\text {Disc }}\left(\boldsymbol{x}, \theta_D\right)
θG,θDminx∈X∑LMLM(x,θG)+λLDisc (x,θD)
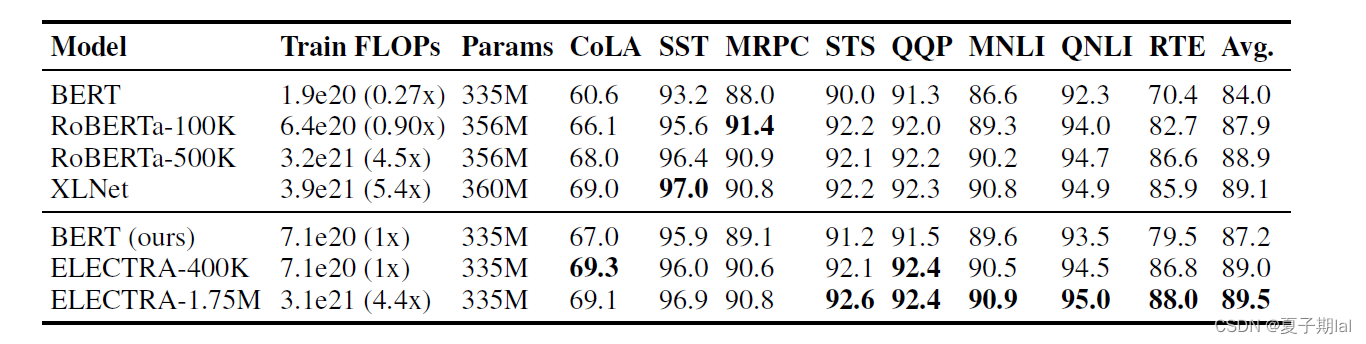
在优化判别器(discriminator)中,计算了所有的token的loss,在常见的MLM模型(如BERT的MLM模型)中只计算了该被遮盖到的token的loss。实验结果证明在下游任务效果中有一定提升。评判指标为GLUE Score。在后续应用于下游任务中,无论是大语言模型还是小语言模型中,都有一定的提升。
discriminator的梯度优化过程中,并不会传递到generator中。而且生成器的目标任务为MLM(掩码预测)任务,判别器的任务为序列标注任务。在同等资源条件下,ELECTRA模型会比BERT等其他模型的效果会好。达到了用尽可能少的资源更好的解决问题。
ELECTRA模型实验结果
小模型在GLUE dev set的效果
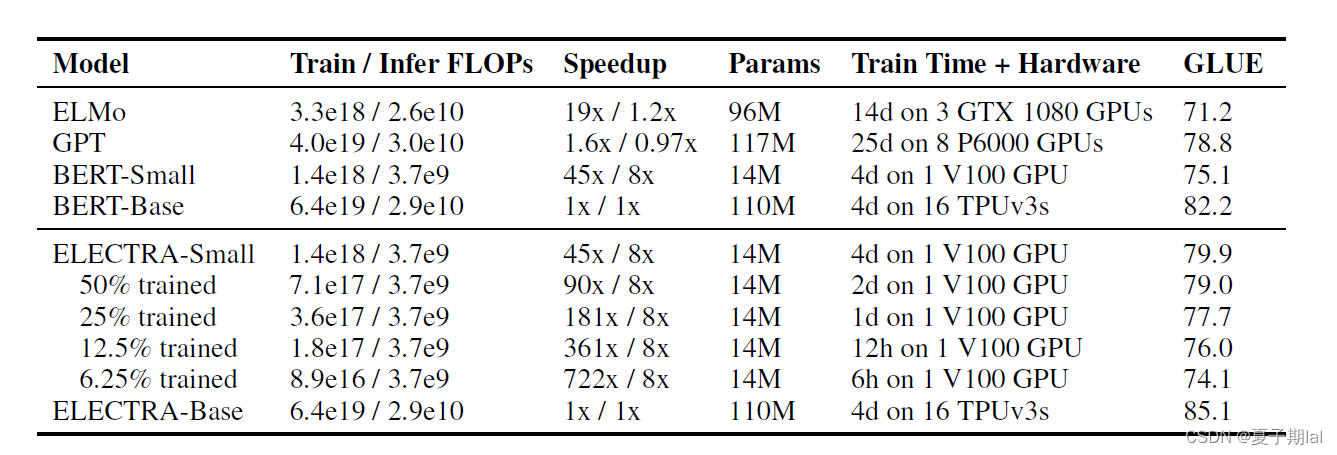
大模型在GLUE dev set的结果
参考
ELECTRA: 超越BERT, 19年最佳NLP预训练模型
huggingface的ElectraForMaskedLM模型
huggingface的bart的mask-fill使用方法
介绍electra模型和bart模型
【论文精读】生成式预训练之BART