常微分方程在诸多研究领域中有着广泛应用，本文希望向大家介绍笔者于近期开发的R包ecode，该包采用简洁易懂的语法帮助大家在R环境中构建常微分方程，并便利地调用R图形接口，研究常微分方程系统的相速矢量场、平衡点、稳定点等解析性质，或进行数值模拟，进行敏感性分析等。

下载与安装

目前，ecode包只有测试版，并已挂载到了github平台上，详见HaoranPopEvo/ecode。安装步骤如下：

1. 在网页中下载名为"ecode_0.0.0.9000.tar.gz"的压缩包。
2. 在RStudio中单击“Tools > Install Packages…”，在弹出的对话框中选择Package Archive (.zip; .tar.gz)，点击Browsing…按钮，在打开的文件浏览对话框中找到文件"ecode_0.0.0.9000.tar.gz"，点击Install按钮，完成安装。

然后将ecode包载入到R环境中：

library(ecode)

构建模型

要构建一个常微分方程系统，首先要利用eode()函数。现考虑构建Lotka–Volterra竞争模型：
$$\begin{gathered} \frac{dx}{dt}=(r_1-a_{11}x-a_{12}y)x,(1) \\ \frac{dy}{dt}=(r_2-a_{21}x-a_{22}y)y,(2) \end{gathered}$$
其中，$x$代表物种1的种群个体数，$x$代表物种2的种群个体数，$r_1,r_2$为种群增长率，$a_{11},a_{12},a_{21},a_{22}$为两物种之间的竞争系数。

该模型中，$x,y$为模型变量，$r_1,r_2,a_{11},a_{12},a_{21},a_{22}$为模型参数。

要在ecode包中构建该模型，可以运行如下代码：

eq1 <- function(x, y, r1 = 4, a11 = 1, a12 = 2) (r1 - a11 * x - a12 * y) * x
eq2 <- function(x, y, r2 = 1, a21 = 2, a22 = 1) (r2 - a21 * x - a22 * y) * y
x <- eode(dxdt = eq1, dydt = eq2)
print(x)
### An ODE system: 2 equations
### equations:
###   dxdt = (r1 - a11 * x - a12 * y) * x 
###   dydt = (r2 - a21 * x - a22 * y) * y 
### variables: x y 
### parameters: r1 = 4, a11 = 1, a12 = 2, r2 = 1, a21 = 2, a22 = 1 
### constraints: x<1000 x>0 y<1000 y>0

其中，等式(1)被表示在R函数对象eq1中，等式(2)被表示在R函数对象eq2中。$x,y$为模型变量，故函数eq1()和eq2()的定义中，参数x, y都没有缺省值。$r_1,r_2,a_{11},a_{12},a_{21},a_{22}$为模型参数，因此在函数eq1()和eq2()的定义中，它们都被赋上了缺省值。本案例中，
$$r_1=4,r_2=1,a_{11}=1,a_{12}=2,a_{21}=2,a_{22}=1$$

R语言中函数的语法
在R语言中，若需要自定义一个函数，其语法为：
fun <- function(x, y, a = 1, b = 2) { x = a + b + x; return(x + y) }
其中，fun为函数对象，function用于声明一个函数，()中的部分为函数头，{}中的内容为函数体。函数头被用于定义形式参数x, y, a, b，其中，形式参数x, y没有缺省值，形式参数a的缺省值为1，形式参数b的缺省值为2。函数体部分用于实施计算，并给出返回值。函数体中有多个语句时，可以分成多行来书写；当函数体只含有一行时，花括号{}可以省略不写。return()函数用于给出函数的返回值。当return()函数被省略时，函数的返回值为函数体中最后一个语句的计算结果。

定义好两个等式后，便可以通过eode()函数创建常微分方程系统。其语法为：

eode(dx1dt = eq1, dx2dt = eq2, ..., constraint = NULL)

其中，dx1dt、dx2dt为等式的名称，eq1、eq2是用于定义等式的函数对象。如果需要定义的常微分方程系统中不止有两个等式，可以在...部分继续添加其他变量。constraint变量用于定义模型变量的范围。若不指定constraint变量，则eode()函数会自动把所有模型变量的范围设置在(0, 1000)的范围内。例如，在上述代码中，调用print()函数打印x的值后，其输出内容含有：

### constraints: x<1000 x>0 y<1000 y>0

这表明，模型变量$x,y$满足$0<x<1000,0<y<1000$。如果要限制$x,y$在(0, 500)内，则可以使用：

x <- eode(dxdt = eq1, dydt = eq2, constraint = c("x<500", "y<500"))
x
### An ODE system: 2 equations
### equations:
###   dxdt = (r1 - a11 * x - a12 * y) * x 
###   dydt = (r2 - a21 * x - a22 * y) * y 
### variables: x y 
### parameters: r1 = 4, a11 = 1, a12 = 2, r2 = 1, a21 = 2, a22 = 1 
### constraints: x<500 x>0 y<500 y>0

如果要限制$x,y$在[100, 500)内，则可以使用：

x <- eode(dxdt = eq1, dydt = eq2, constraint = c("x<500", "y<500", "x>=100", "y>=100"))
x
### An ODE system: 2 equations
### equations:
###   dxdt = (r1 - a11 * x - a12 * y) * x 
###   dydt = (r2 - a21 * x - a22 * y) * y 
### variables: x y 
### parameters: r1 = 4, a11 = 1, a12 = 2, r2 = 1, a21 = 2, a22 = 1 
### constraints: x<500 x>=100 y<500 y>=100

eode()函数的返回对象的类别是"eode"。这种类别的对象是ecode包中的核心对象。这种对象用于存放有关常微分方程系统的信息，并得以调用其他复杂的函数，来研究该常微分方程系统的性质。

class(x)
### [1] "eode"

相速矢量场

模型构建完成后，就可以简单地调用plot()函数，绘制模型的相速矢量场，

plot(x)

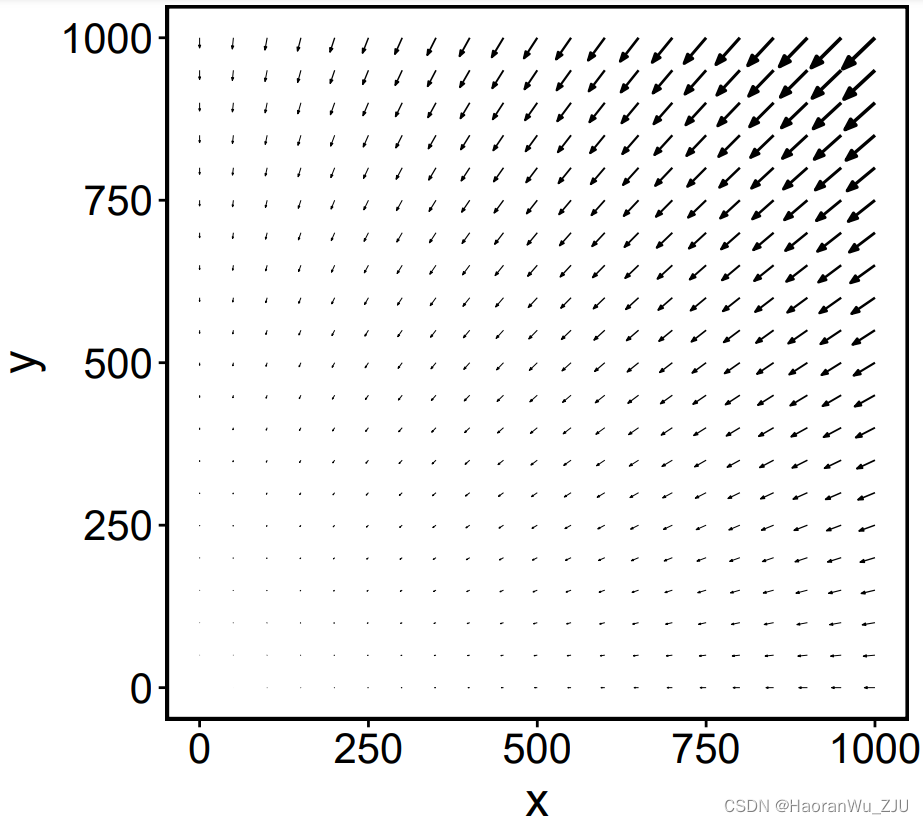
图中的横轴、纵轴分别代表模型变量$x,y$的值，每个箭头代表系统在某一相点$(x,y)$时的相速矢量。箭头的长短代表相速矢量的大小，箭头越长代表相速矢量的绝对值越大，即相点在该处的运动速度很快。箭头的方向代表相点在该处时的运动方向。该图表明，相点似乎无论如何都会沿着原点$(0,0)$处运动。

修改模型变量的范围

我们可能需要进一步观察$x,y\in (0,2)$时的相速矢量场。这时，我们可以通过eode_set_constraint()函数更改模型变量的限制条件：

x <- eode_set_constraint(x, c("x<2", "y<2"))
x
### An ODE system: 2 equations
### equations:
###   dxdt = (r1 - a11 * x - a12 * y) * x 
###   dydt = (r2 - a21 * x - a22 * y) * y 
### variables: x y 
### parameters: r1 = 4, a11 = 1, a12 = 2, r2 = 1, a21 = 2, a22 = 1 
### constraints: x<2 x>0 y<2 y>0

随后重新绘制系统的相速矢量场：

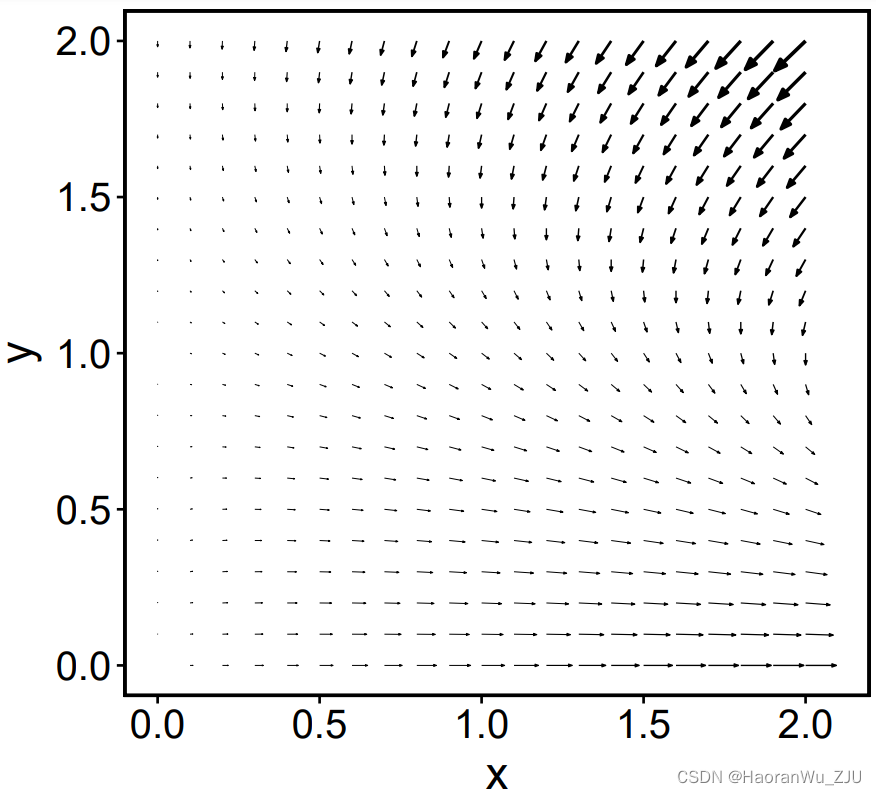
可以发现，当相点较小时（例如$(x,y)=(1,1)$），相点并不会朝着$(0,0)$点运动，而是沿着$x$增大、$y$减小的方向移动。

如何引用

Wu, H. (2023). ecode: An R package to investigate community dynamics in ordinary differential equation systems. bioRxiv, 2023-06.

原文见bioRxiv。