---

【获取资源请见文章第5节：资源获取】

---

1. 车间布局优化

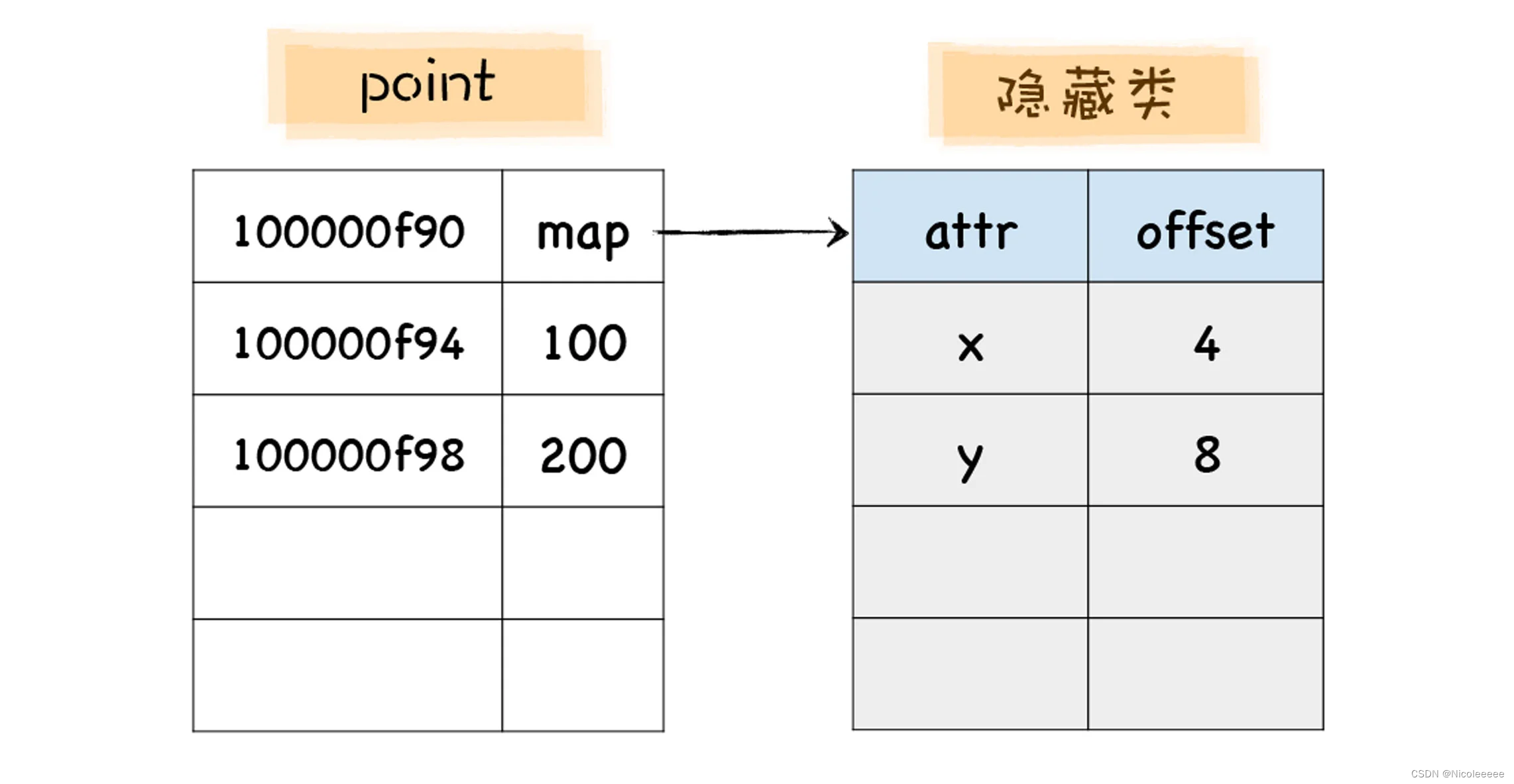
车间设施布置的规划一直是工业工程领域不断研究和探索的内容，其中最具代表性之一的是系统布置设计(system layout planning，SLP) 方法。作为一种经典且有效的方法，其为设施布置提供了很好的改善思路，但在长期的发展中也存在一些不可避免的缺点，如计算结果不够精确，很难确保计算结果较优且受人员主观因素的影响较大等。

随着计算机技术的快速发展，基于计算机技术的启发式算法在数据处理、数学建模、运算速度等方面相比传统方法具备更大的优势，因此在用 SLP 方法布置时完全可以将大量计算求解的工作交由计算机处理，从而可大幅度提高布置效率和布置结果的精确性。

目前设施布置设计的模型与算法已经比较成熟，常见的有遗传算法、蚁群算法、模拟退火算法等启发式算法。

2. 基于GA的布局优化模型

车间布局优化模型如下图所示：

模型目标函数为搬运费用最小化及非物流关系最大化。

假设布置方案为X，i 和 j 为该方案的作业单位，两者距离用$d_{ij}$表示，搬运量用$f_{ij}$表示，可得距离矩阵及物流量矩阵，进而求得物料搬运成本表达式如下：
$$C_1=\sum _{i=1}^m\sum _{j=1}^m{c}_{ij}{f}_{ij}{d}_{ij}$$
式中，$C_1$为总搬运成本；$c_{ij}$为各单位之间的搬运成本。非物流关系表达式为：
$$C_2=\sum _{i=1}^m\sum _{j=1}^m{T}_{ij}{b}_{ij}$$
式中，$C_2$为非物流关系总和；$T_{ij}$为作业单位之间非物流关系的紧密程度。

由此可得两个基本目标，即$C_1$的最小化和$C_2$的最大化，从而构建双目标函数如下：
$$min{C}_1=\sum _{i=1}^m\sum _{j=1}^m{c}_{ij}{f}_{ij}{d}_{ij}$$
$$max{C}_2=\sum _{i=1}^m\sum _{j=1}^m{T}_{ij}{b}_{ij}$$
为方便求解，将双目标函数$C_1$和$C_2$进行合并，得到单目标函数$C$表达式如下：
$$minC=\sum _{i=1}^m\sum _{j=1}^m{c}_{ij}{f}_{ij}{d}_{ij}-\sum _{i=1}^m\sum _{j=1}^m{T}_{ij}{b}_{ij}$$

此单目标函数仍需进行标准化处理，并且还需以惩罚函数加以限制，

3. 部分代码展示

%% 物料搬运成本最小化和非物流关系最大化的合并目标函数
function [fit,Z1,Z2] = Fitness(P,LW,D,A,C,T,L,W,big)
dmax = max([L W]);
gap = 3;
%% SECTION TITLE
% DESCRIPTIVE TEXT
K = size(P,1);   % 设施数量
%% 计算关联因子
dB = zeros(K);
for i = 1 : K
    for j = i + 1 : K
        if D(i,j) <= dmax / 6
            dB(i,j) = 1;
        elseif D(i,j) <= dmax / 3
            dB(i,j) = 0.8;
        elseif D(i,j) <= dmax / 2
            dB(i,j) = 0.6;
        elseif D(i,j) <= dmax * 2 / 3
            dB(i,j) = 0.4;
        elseif D(i,j) <= dmax * 5 / 6
            dB(i,j) = 0.2;
        else
            dB(i,j) = 0;
        end
        dB(j,i) = dB(i,j);
    end
end
%% 目标函数1
Z1 = 0;
for i = 1 : K - 1
    for j = i + 1 : K
        Z1 = Z1 + C(i,j) * A(i,j) * D(i,j);
    end
end
%% 目标函数2
Z2 = 0;
for i = 1 : K - 1
    for j = i + 1 : K
        Z2 = Z2 + T(i,j) * dB(i,j);
    end
end
%% 归化因子计算
u1 = 0;
 for i = 1 : K - 1
    for j = i + 1 : K
        u1 = u1 + C(i,j) * A(i,j) * dmax;
    end
 end
u1 = 1 / u1;
u2 = 0;
for i = 1 : K - 1
    for j = i + 1 : K
        u2 = u2 + T(i,j);
    end
end
u2 = 1 / u2;
%% 边界约束1
t = 0;
for i = 1 : K
    if P(i,1) - LW(i,1) / 2 < gap ||  P(i,1) + LW(i,1) / 2 > L - gap
        t = t + 1;     % x方向不满足边界要求
    end
    if P(i,2) - LW(i,2) / 2 < gap ||  P(i,2) + LW(i,2) / 2 > W - gap
        t = t + 1;     % y方向不满足边界要求
    end
end
%%
dtag = (D == big);
dtn = sum(sum(dtag));
t = t + dtn;
%% 适应度
w1 = 3 / 4;
w2 = 1 / 4;
fit = w1 * u1 * Z1 - w2 * u2 * Z2 + 10000000000 * t;

4. 仿真结果展示

5. 资源获取

可以获取完整代码资源。