目录

并查集概念

合并

 查找集合的数量

并查集类代码实现

---

并查集概念

并查集和堆一样，都是通过数组来实现树的节点映射，不过并查集作用是，把一堆数据分为不同的几个小集合

不过并查集是森林的概念，并查集的学习可以帮助我们去更好的学习图这个数据结构

这里我们举一个例子：

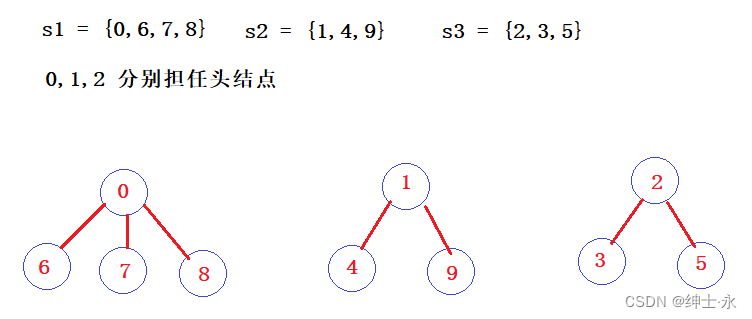
假设我们有一个旅游团，一共有十个人，编号是0~9；

其中 s1 = {0,6,7,8} 这几个人来自湖北

        s2 = {1,4,9} 这几个人来自四川

        s3 = {2,3,4} 这几个人来自北京

上面我们把十个人分为了不同几个小组，他们来自不同的地方，吃的口味自然不同，于是就分别让0,1,2这三个人担任组长，带领各自的队伍去吃饭。

队长可以抽象的理解为头结点，组员理解为各自的孩子结点

数组的初始化规则定义如下：

1.每一个下标存放自己的双亲结点下标

2.如果该结点是双亲结点，存放一个负数，我们可以顺便存放这棵树的结点个数

特点:

• 一个位置是负数，那他就是树的根，这个绝对值就是棵树的结点个数
• 一个位置值是负数那他就是双亲的下标

合并

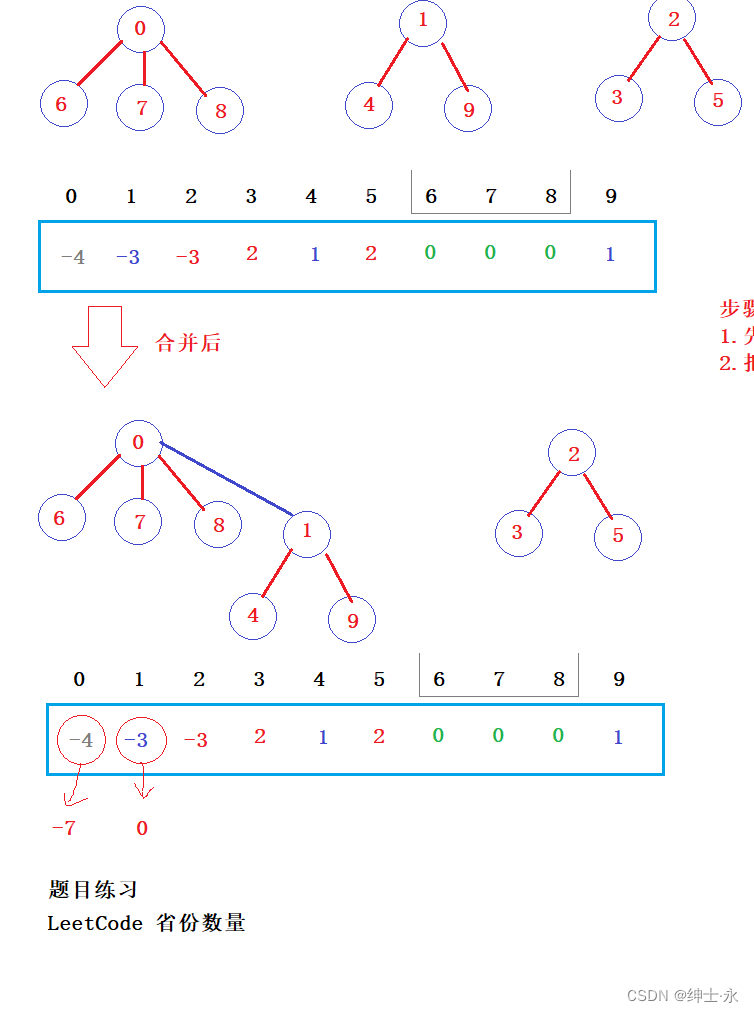
我们假设上面的s1和s2发生了合并，咋办呢？

步骤：

• 先找到两个需要合并集合的双亲结点
• 再把集合2的根下标存放的值+=集合1的根下标，在把集合2的根下标存放的值置为集合1的根

 查找集合的数量

我们只需要将整个数组遍历一遍，找到为负数的位置有多少个，即集合的数量

并查集类代码实现

class UnionFindSet
{
public:
	UnionFindSet(size_t n)
		:_ufs(n, -1)
	{}
	
	void Union(int x1, int x2)
	{
		// 1.先找根
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);
		//如果在一个集合就没有必要去合并
		if (root1 == root2)
		{
			return;
		}
		//将集合2合并到集合1
		_ufs[root1] += _ufs[root2];
		_ufs[root2] = root1;
	}

	// 找根/双亲
	int FindRoot(int x)
	{ 
		int parent = x;
		while (_ufs[parent] >= 0)
		{
			parent = _ufs[parent];
		}

		return parent;
	}

	bool InSet(int x1, int x2)
	{
		return FindRoot(x1) == FindRoot(x2);
	}

	size_t SetSize()
	{
		size_t size = 0;
		for (size_t i = 0; i < _ufs.size(); ++i)
		{
			if (_ufs[i] < 0)
			{
				++size;
			}
		}

		return size;
	}

private:
	vector<int> _ufs;
};