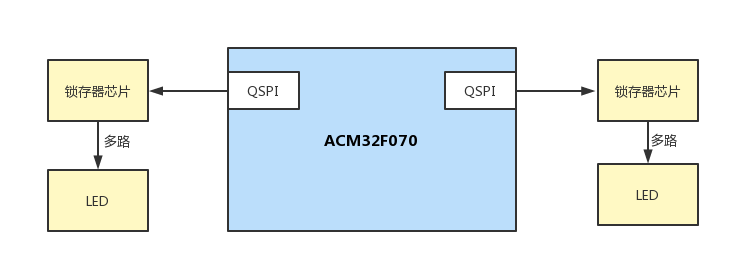
引言

全量参数微调在LLM背景下由“不方便”演变为“不可行|高昂成本”，基于“收敛的模型参数可以压缩到低维空间”的假设：

the learned over-parametrized models in fact reside on a low intrinsic dimension.

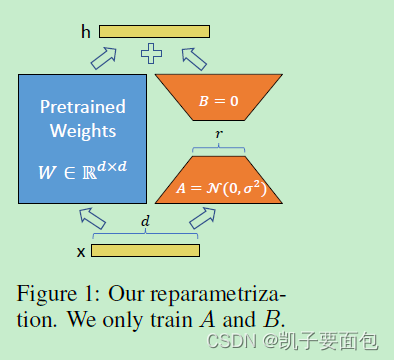
作者提出LORA（Low Rank Adaptation）方法，其本质如下图所示：

$h=Wx$，其中$x$是输入变量，$h$是输出变量，$W$是预训练模型参数，如何在保持$W$不变的条件下，改变输出变量$h$的值呢？可以引入一个新的模型权重变量$Z$， 得到$h=(W+Z)x$ ，注意这里的变量$Z$必须与变量$W$是同维度的。但如果直接使用$Z$，将毫无意义，因为在LLM中，变量$Z$将使得模型规模翻一倍。因此基于假设，作者提出将变量$Z$分解为两个低维度的变量$A$与$B$，并满足$Z=AB$、变量$A$与$B$的秩（RANK）远小于变量$Z$。在初始化时，变量$A$满足正太分布、变量$B$为零矩阵。这个思想与ALBERT中分解Embedding层的思想非常相似，只是LORA的作用范围主要应用在LLM中的注意力层。

LORA方法使得其具有以下优点：

• 共享预训练模型参数，降低下游任务开发部署成本。
• 由于仅需微调一部分参数，因此降低了训练LLM的门槛与成本。
• 线性结构设计$W+Z$使得模型并没有引入额外的计算开销——部署模型时，可以合并冻结的预训练参数与新引入的模型参数。
• 不同于Prompt tuning类方法，不占用模型有效输入的长度。
• 可以与Prompt tuning类方法结合使用。

注意在LORA中有两个重要的超参数，第一个是秩超参数$r$，如果$r$的取值与变量$W$的秩值相同，则相当于Fine-tuning同等规模的模型参数，因此参数$r$的值应该远小于变量$W$的秩值。另一个超参数为$\alpha$，超参数$\alpha$会对新引入的权重进行$\frac{\alpha }{r}$缩放，控制新引入权重对预训练权重的影响程度。