什么是数据结构
数据结构的研究对象
- 研究一组有特定关系的数据的存储与处理
- 通过抽象的方法
数据结构的研究内容
-
数据之间的逻辑关系:存储实现(如何存储某种逻辑关系)
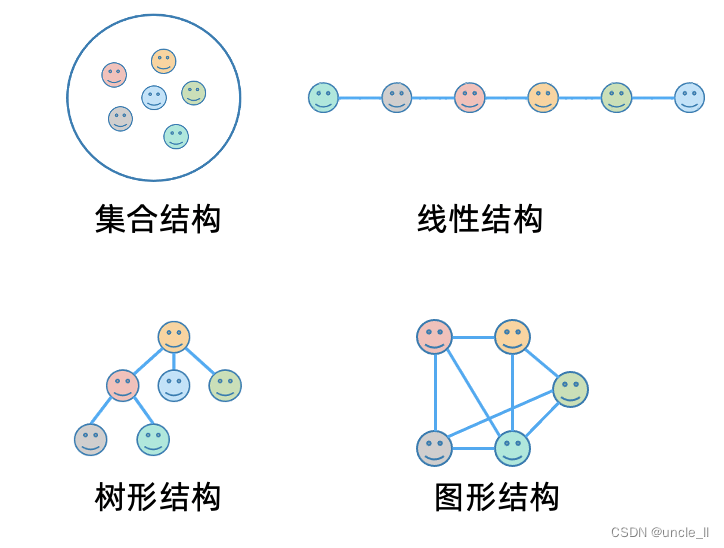
- 集合结构:数据元素放在一起,但是元素间没有关系
- 线性结构:数据元素的有序序列,每个元素有一个前趋和一个后继
- 树形结构:层次关系的数据,除了根元素,每个元素有且只有一个前趋,后继数目不限
- 图形结构:元素之间相互关联,每个元素可以有多个前趋和后继
-
关系对应的操作:运算实现(在这种存储模式下,如何实现相关操作)
- 创建:创建空的数据结构
- 清除:清空数据结构
- 插入:在指定位置插入新元素
- 删除:删除某个元素
- 搜索:搜索满足特定条件的元素
- 更新:修改某个元素的值
- 访问:访问数据结构中的某个元素
- 遍历:按照某种次序,访问每个元素有且只有一次
-
存储实现
- 需要储存的信息
- 一组数据元素
- 数据元素之间的关系
- 物理结构
- 存储结点
- 数据元素之间的关系的存储
- 附加信息
- 关系的存储
- 顺序存储
- 链接存储
- 哈希存储
- 索引存储
- 需要储存的信息
-
运算实现
- 操作怎么实现
- 每个运算对应一个算法
- 每个算法用一个函数表示
- 每个数据结构有一组函数
- 操作怎么实现
-
时间性能
- 时间性能的衡量
- 标准操作
- 时间复杂度
- 最好情况的时间复杂度
- 最坏情况的时间复杂度
- 平均情况的时间复杂度
- 大O表示法(上界)
- 两个定理
- 求和定理
- 求积定理
-
空间性能
- 空间复杂度
- 算法处理过程中所需的额外工作量
- 一般按最坏情况处理
- 用大O表示法
- 空间复杂度
-
算法优化问题提出
- 慢慢分析,逐步优化
- 最大连续子序列和问题
-
O ( N 3 ) O(N^3) O(N3)的算法
- 枚举法
-
O ( N 2 ) O(N^2) O(N2)的算法
- 枚举子序列
-
O ( N l o g N ) O(NlogN) O(NlogN)的算法
- 分治法
- 情况1:答案位于前半部,可递归计算
- 情况2:答案位于后半部,可递归计算
- 情况3:答案从前半部开始但在后半部结束
- 情况3的解决
- 从两半部分的边界开始
- 通过从右到左的扫描来找到左半段的最长序列
- 从左到右的扫描找到右半段的最长序列
- 把这两个子序列组合起来,形成跨越分割边界的最大连续子序列
- 算法总结
- 递归地计算整个位于前半部的最大连续子序列
- 递归地计算整个位于后半部的最大连续子序列
- 通过两个连续循环,计算从前半部开始在后半部结束的最大连续子序列的和
- 选择三个值中的最大值
- 分治法
-
O(N)的算法
- 在枚举法的基础上改进
- 现象:和为负的子序列不可能是最大连续子序列的开始部分
- 结论:当检测出一个负的子序列时,可以让start直接增加到j+1
- 在枚举法的基础上改进
数据结构的存储实现
-
需要储存的
信息
- 一组数据元素
- 数据元素之间的关系
-
物理结构
- 存储结点:一个简单变量、结构体变量或者对象
- 存储数据元素之间的关系:用结点间的关系来表达
- 存储附加信息:便于运算的“哑结点”
-
如何存储
元素及其关系
- 顺序存储:用存储的位置表示元素之间的关系,主要用数组实现
- 链接存储:用指针显式指出元素之间的关系,如链表
- 哈希存储:主要用于表示集合这种元素间没有关系的结构,方便查找
- 索引存储:分为数据区和索引区,在索引区存放关系
数据结构的运算实现
- 操作怎么实现
- 每个运算对应一个算法
- 每个算法用一个函数表示
- 每个数据结构有一组函数表示其对应的操作
算法优化
算法优化指的是优化算法的时间性能和空间性能。需要慢慢分析,逐步优化。
以最大连续子序列和问题为例来看算法优化问题。
给定整数序列,寻找最大的子序列和,例如,对于序列{-2, 11, -4, 13, -5, 2},答案是20。
- O ( N 3 ) O(N^3) O(N3)算法:枚举法:
这是最直观的算法。用起点和终点来确认一个子序列,这样我们就可以用两层的嵌套循环,枚举出所有的子序列:
int maxSubsequenceSum(int a[], int size, int &start, int &end) {
int maxSum = 0;
// 枚举起点 i
for (int i = 0; i < size; i++ ) {
// 枚举终点 j
for( int j = i; j < size; j++ ) {
int thisSum = 0;
// 计算i到j的子序列和
for( int k = i; k <= j; k++ ) thisSum += a[ k ];
// 如果是最大的,存下这个子序列的起点和终点以及最大的和
if( thisSum > maxSum ) {
maxSum = thisSum;
start = i; end = j;
}
}
}
return maxSum;
}
- O ( N 2 ) O(N^2) O(N2) 算法:枚举子序列
在枚举的时候,i到 j+1 这个子序列的和,没必要再用一个for循环,可以直接在 i到 j 这个子序列的和上再加1个数,省略到最里层的循环。
int maxSubsequenceSum(int a[], int size, int &start, int &end) {
int maxSum = 0;
for (int i = 0; i < size; i++ ) {
int thisSum = 0;
for( int j = i; j < size; j++ ) {
// 直接在之前的计算结果上加上一个数,就能得到i到j的子序列和
thisSum += a[ j ];
if( thisSum > maxSum ) {
maxSum = thisSum;
start = i; end = j
}
}
}
return maxSum;
}
- O ( N l o g N ) O(NlogN) O(NlogN) 算法:分治法
分成不同的情况来解决:
- 情况1:最大和子序列位于前半部,可递归计算
- 情况2:最大和子序列位于后半部,可递归计算
- 情况3:最大和子序列从前半部开始但在后半部结束
- 从两半部分的边界开始
- 通过从右到左的扫描来找到左半段的最长序列
- 从左到右的扫描找到右半段的最长序列
- 把这两个子序列组合起来,形成跨越分割边界的最大连续子序列
int maxSum(int a[ ], int left, int right , int &start, int &end) {
int maxLeft, maxRight, center;
int leftSum = 0, rightSum = 0;
int maxLeftTmp = 0, maxRightTmp = 0;
int startL , startR, endL, endR;
// 递归的终止条件
if (left == right) {
start = end = left;
return a[left] > 0 ? a[left] : 0;
}
center = (left + right) / 2;
// 递归地计算整个位于前半部的最大连续子序列
maxLeft = maxSum(a, left, center, startL, endL);
// 递归地计算整个位于后半部的最大连续子序列
maxRight = maxSum(a, center + 1, right, startR, endR);
// 计算从前半部开始在后半部结束的最大连续子序列的和
// 选择三个值中的最大值
if (maxLeft > maxRight )
if (maxLeft > maxLeftTmp + maxRightTmp) {
start = startL;
end = endL;
return maxLeft;
}
else return maxLeftTmp + maxRightTmp;
else
if (maxRight > maxLeftTmp + maxRightTmp) {
start = startR;
end = endR;
return maxRight;
}
else return maxLeftTmp + maxRightTmp;
}
- O(N) 算法:在枚举法的基础上改进
- 现象:和为负的子序列不可能是最大连续子序列的开始部分
- 结论:当检测出一个负的子序列时,可以让start直接增加到j+1
int maxSubsequenceSum(int a[], int size, int &start, int &end) {
// starttmp用于保存前面的最优方案
int maxSum, starttmp, thisSum;
start = end = maxSum = starttmp = thisSum = 0;
for( int j = 0; j < size ; ++j ) {
thisSum += a[j];
if ( thisSum <= 0 ) {
thisSum = 0;
starttmp = j+1;
} else if (thisSum > maxSum ) {
maxSum = thisSum;
start = starttmp;
end = j;
}
}
return maxSum;
}






![Qt Xml文件的创建和解析[xml和dom方式]](https://img-blog.csdnimg.cn/b381a98a8e47447790a319816442ccc6.png)