[BOI2009] Radio Transmission 无线传输

题目描述

给你一个字符串 $s_1$，它是由某个字符串 $s_2$ 不断自我连接形成的（保证至少重复 $2$ 次）。但是字符串 $s_2$ 是不确定的，现在只想知道它的最短长度是多少。

输入格式

第一行一个整数 $L$，表示给出字符串的长度。

第二行给出字符串 $s_1$ 的一个子串，全由小写字母组成。

输出格式

仅一行，表示 $s_2$ 的最短长度。

样例 #1

样例输入 #1

8
cabcabca

样例输出 #1

3

提示

样例输入输出 1 解释

对于样例，我们可以利用 $\text{abc}$ 不断自我连接得到 $\text{abcabcabc}$，读入的 $\text{cabcabca}$，是它的子串。

规模与约定

对于全部的测试点，保证 $1<L\le 10^6$。

分析

#include<bits/stdc++.h>
using namespace std;
int m;
void getfail(char *p,int *f){
	m=strlen(p+1);
	f[1]=0;int j=0;
	for (int i=1;i<m;i++){
		while(j and p[j+1]!=p[i+1]) j=f[j];
		if (p[j+1]==p[i+1]) ++j;
		f[i+1]=j;
	}
	return;
}
char a[1000000];int f[100000];
int main(){
	cin>>a+1;
	getfail(a,f);
	for (int i=1;i<=m;i++) cout<<a[i]<<' ';
	cout<<endl;
	for (int i=1;i<=m;i++) cout<<i<<' ';
	cout<<endl;
	for (int i=1;i<=m;i++) cout<<f[i]<<' ';
	
	return 0;
} 

上面是一个推算过程，展现了KMP算法的预处理过程，譬如：

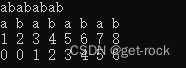
这是原数组，下标，与失配的关系，具体可以说：我们输入字符串S，S具有一定的周期串T，那么对$$m-f[m],m=|S|$$
可以发现在此串中，周期串"ab"的长度为2，而$8-f[8]$也是为2，我们便得到了一个结论：
$$m-f[m]=|T|$$(想一想，为什么）

#include<bits/stdc++.h>
using namespace std;
int n,m;
void getfail(char *p,int *f){
	m=strlen(p+1);
	f[1]=0;int j=0;
	for (int i=1;i<m;i++){
		while(j>0 and p[j+1]!=p[i+1]) j=f[j];
		if (p[j+1]==p[i+1]) ++j;
		f[i+1]=j;
	}
	return;
}
void find(char *t,char *p,int *f,int &ans){
	getfail(p,f);
	int j=0;
	for (int i=0;i<n;i++){
		while(j>0 and p[j+1]!=t[i+1]) j=f[j];
		if (p[j+1]==t[i+1]) j++;
		if (m==j) 
		{	
			j=0;
			ans++;
		}
	}
}
char* a=new char[10000000];
int*  f=new int[10000000];
int main(){
	cin>>n;
	scanf("%s",a+1);
	getfail(a,f);
	cout<<n-f[n];
	return 0;
} 

通过此公式，便通过此题了