Open-World Class Discovery with Kernel Networks (ICDM 2020)

摘要

我们研究了一个开放世界类发现问题，在这个问题中，训练样本是来自旧类有标签的样本，而我们从没有标记的测试样本中发现新的类。解决这一范式有两个关键的挑战:(a)将知识从旧类转移到新类，(b)将从新类学到的知识整合到原始模型中。我们提出了一种深度学习框架——类发现扩展核网络(CD-KNet-Exp)，该框架利用Hilbert Schmidt独立性准则将有监督信息和无监督信息系统地连接在一起，从而适当地提取旧类中的知识以发现新类。与竞争方法相比，CD-KNet-Exp在三个公开可用的基准数据集和具有挑战性的真实世界无线电频率指纹数据集上显示优越的性能。

希尔伯特施-密特独立性准则

希尔伯特-施密特独立准则(Hilbert schimidt Independence Criterion, HSIC)是一种两个随机变量之间的统计依赖性度量方式。就像互信息一样（Mutual Information, MI），能够捕捉到两个随机变量之间的非线性依赖。和互信息相比，该独立性判断经上验计算简单，避免了联合概率分布的显式估计。考虑到这一点，它被广泛应用到不同领域，例如特征选择、维度约减、选择聚类以及深度聚类。
考虑到独立同分布的样本元组$\{(p_i,q_i){\}}_{i=1}^N$，让每一行元素分布对应相应的样本，构建矩阵$P\in {\mathbb{R}}^{N\times d}$和$Q\in {\mathbb{R}}^{N\times c}$，并令$k_p:{\mathbb{R}}^d\times {\mathbb{R}}^d\to \mathbb{R}$和$k_q:{\mathbb{R}}^c\times {\mathbb{R}}^c\to \mathbb{R}$分别作为$p_i,q_i$的核函数。比如说高斯核以及线性核：


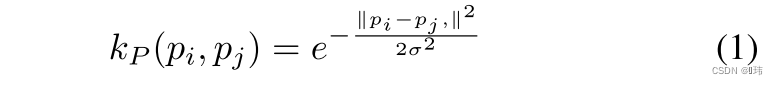
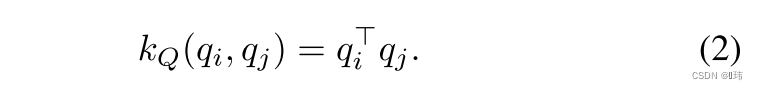
进一步定义$K_P,K_Q$作为$P,Q$的核矩阵，其中 K P = { k P ( p i , p j ) } i , j } ∈ R N × N K_P=\{k_P(p_i,p_j)\}_{i,j}\} \in \mathbb{R}^{N \times N} KP​={kP​(pi​,pj​)}i,j​}∈RN×N， K Q = { k Q ( q i , q j ) } i , j } ∈ R N × N K_Q=\{k_Q(q_i,q_j)\}_{i,j}\} \in \mathbb{R}^{N \times N} KQ​={kQ​(qi​,qj​)}i,j​}∈RN×N。
$P,Q$之间的HSIC在核函数$k_P,k_Q$的作用下一般可以定义为以下形式：

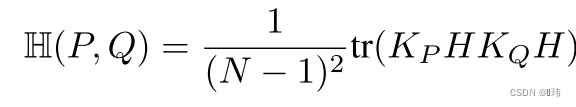
监督学习设置

假设数据矩阵KaTeX parse error: Expected 'EOF', got '}' at position 16: X \in \mathbb(R}̲_{N \times d_0}包含$N$个每行$d_0$维的样本，并且标签矩阵 Y ∈ { 0 , 1 } N × m Y \in \{0,1\}_{N \times m} Y∈{0,1}N×m​表示$m$个标签的one hot编码形式。我们可以通过HSIC以监督学习的设置进行维度缩减。我们可以通过最大化输入数据的非线性特征映射和标签之间的依赖程度来实现上述目的。将$K_X$设置为高斯核，$K_Y$设置维线性核，则该优化问题如下形式：

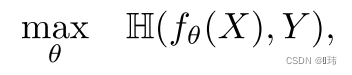
通过最大化两者之间的依赖，直觉上，这会迫使特征提取器最大化依赖标签。同时也缩减了维度，因此一个浅层分类器可以被用来从低维表征中学习标签。

无监督学习设置

在无监督的情况下，我们可以利用HSIC最大化输入数据的非线性映射和一个可学习的潜在簇嵌入$U$（可以先简单理解为一种聚类方法给出的伪标签）之间的依赖来进行无监督学习，输入数据的采用一个归一化的高斯核函数：

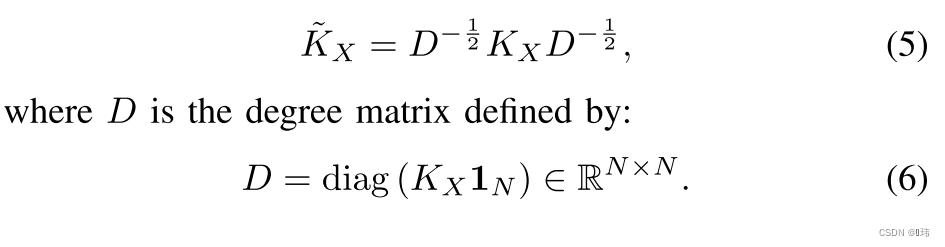
对于$U$也采用线性核，按照以下优化问题优化：

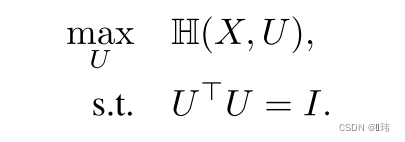
联系之前通过监督训练得到的特征提取器，上述优化问题可以改写成以下形式：

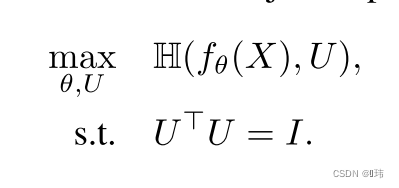
类别发现的核网络方法

该部分，我们提供了我们所提方法的概述，称为Class Discovery Kernel Network(CD-KNet)，用于解决开放世界中新类发现的问题。并展示了一个神经网络的拓展策略来引入发现的新类中的信息反馈。

CD-KNet with Expansion概述

该方法将开放世界新类发现问题分成三个阶段：

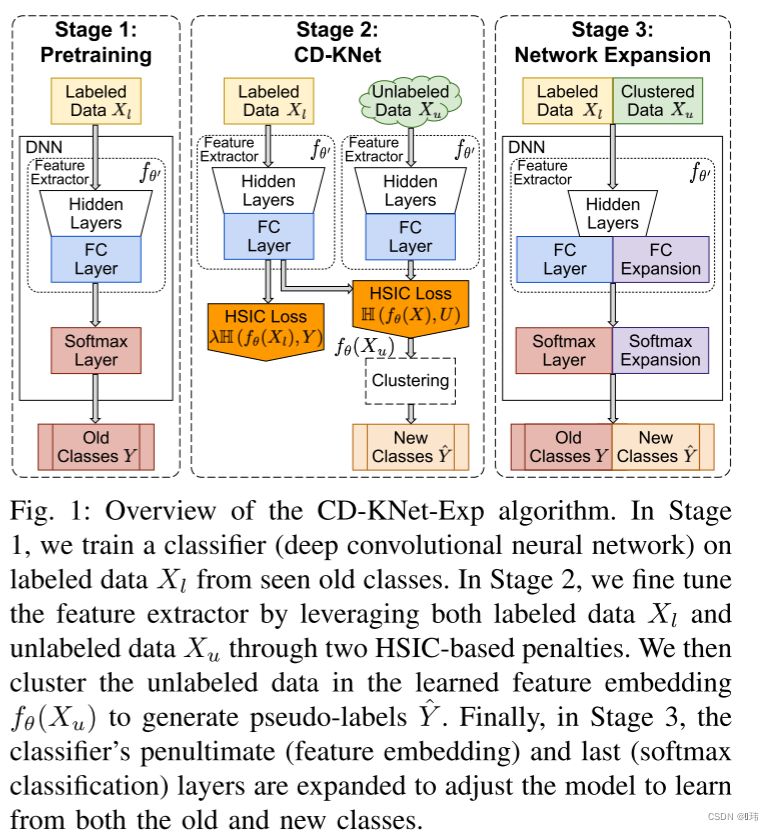
第一阶段：在有标签数据集上训练一个特征提取器，将输入数据映射为$d$维的表征向量，再加一个softmax分类器，通过标准损失函数训练（平方误差，交叉熵等）

第二阶段：通过第一阶段，学习得到一个特征提取器。第二阶段的目的就是发现新的类别。但是从标注数据学到的特征嵌入空间可能存在较大的偏差，从而导致不能很好的泛化到无标签数据上。
在我们的工作中，我们没有直接使用从第一阶段获得的特征提取器，而是对它进行了更新，迫使它同时适应有监督的旧类和无监督的新类。

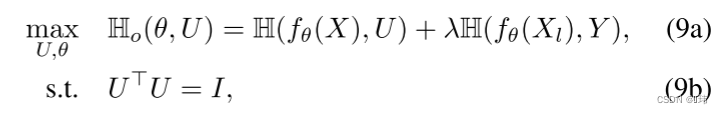
直观地说，第一项鼓励所有类别分离（旧的和新的），两者都应该是“可聚类”的，就像对低秩正交矩阵u的高度依赖所捕获的那样。第二项引入监督信息，确保潜在嵌入保持旧类之间的分离，因为旧类与其标签保持对齐。
作为第二阶段的最后一步，我们取新数据集的潜在嵌入，并对其进行聚类。更详细地说，在收敛性的基础上，特征提取器被细化到一定程度，融合了有标记的旧类和无标记的新类的信息，形成了一个能够很好地分离新旧类的特征空间。然后，我们可以执行任何聚类方法，例如K-means，以得到簇分配。注意，这些簇构成了我们的新类。我们将所得到的聚类标签称为伪标签。

第三阶段：DNN可以看作是一个特征提取器和一个softmax层的组合，例如，最后的稠密层采用softmax激活。扩展网络的一个简单的启发式方法是，通过添加与我们发现的新类数量相同的节点来扩展softmax层。这一策略在以往的一些研究中已经在不同的语境下被采用，如迁移学习。
然而，我们还需要考虑特征提取器的表示能力。当旧类和新类合并时，特征提取器自然需要更大的容量，即更多的参数，以表示更复杂的数据集。Zeiler等人认为，DNN中较浅层通常提取不同任务之间共同的一般性、抽象特征，而较深层则捕获与任务/数据集密切相关的特定特征。因此我们决定只扩展特征提取器的最后一层，即整个DNN的倒数第二层，其余的特征提取器保持不变。在实践中，我们发现扩展浅层并不会对最终性能产生太大的影响，因为在浅层很容易发生过拟合。
为了达到这个目的，在第三阶段，我们在最后一层加入等同于新类的数目的输出节点，在倒数第二层加入25%的神经元来扩展网络。然后通过标注数据和伪标注数据对扩展模型进行微调。特别是，该模型在未标注数据上进行了微调，用伪标签监督加入了新的类。此外，我们还加入了部分p%的旧类数据，以加强之前从旧类上看到的知识。

emmmm

不知道去掉HSIC这块会怎样，如果修改第二阶段变成：通过聚类方法得到伪标签，然后直接和标注数据一起训练模型，然后动态修改无标注数据的聚类标签，如果改成这样不知道会怎样。我想通过HSIC提高有标签数据中输入和类别之间的依赖，以及无标签输入和伪标签之间的依赖，为什么不直接映射过去，让两者相等呢？