原题链接：

Problem - 1737C - Codeforces

题目描述：

The problem, which involves a non-standard chess pieces type that is described below, reads: given 33 white crickets on a n⋅nn⋅n board, arranged in an "L" shape next to each other, there are no other pieces on the board. Ela wants to know with a finite number of moves, can she put any white cricket on the square on row xx, column yy?

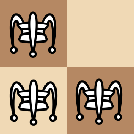
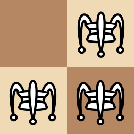
An "L"-shape piece arrangement can only be one of the below:

For simplicity, we describe the rules for crickets on the board where only three white crickets are. It can move horizontally, vertically, or diagonally, but only to a square in some direction that is immediately after another cricket piece (so that it must jump over it). If the square immediately behind the piece is unoccupied, the cricket will occupy the square. Otherwise (when the square is occupied by another cricket, or does not exist), the cricket isn't allowed to make such a move.

See an example of valid crickets' moves on the pictures in the Note section.

Input

Each test contains multiple test cases. The first line contains the number of test cases tt (1≤t≤1041≤t≤104). The description of the test cases follows.

The first line of each test case contains nn (4≤n≤1054≤n≤105) — denotes the size of the chessboard.

The second line of each test case contains 6 numbers: r1r1, c1c1, r2r2, c2c2, r3r3, c3c3 (1≤r1,c1,r2,c2,r3,c3≤n1≤r1,c1,r2,c2,r3,c3≤n) — coordinates of the crickets. The input ensures that the three crickets are arranged in an "L" shape that the legend stated.

The third line of each test case contains 2 numbers: xx, yy (1≤x,y≤n1≤x,y≤n) — coordinates of the target square.

Output

For each test case, print "YES" or "NO" to denotes whether Ela can put a cricket on the target square.

题目大意：

略（点题目链接，然后复制题目自行翻译吧，挺麻烦的）。

解题思路：

分类讨论：

1、四种特殊情况，L紧贴角落，则只能平移一行的两个或者一列的两个

2、常规情况，平移L，如果目标点不在一个完整的区域中，可以先到达邻近的区域，再进行一至两步操作到达终点，如果目标正好在2*2区域的孔雀位置，则无解

代码（CPP）：

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 1e3 + 10;
const int INF = 0x3fffffff;

void solve()
{
    int n, a[4][2];
    cin >> n;
    map<pair<int, int>, int> mp;
    for (int i = 1; i <= 3; i++)
    {
        cin >> a[i][0] >> a[i][1];
        mp[{a[i][0], a[i][1]}]++;
    }
    int x, y;
    cin >> x >> y;

    // 四种特殊情况，L紧贴角落
    if(mp[{1, 1}] && mp[{1, 2}] && mp[{2, 1}])
    {
        if(x == 1 || y == 1)
            cout << "YES\n";
        else
            cout << "NO\n";
        return;
    }
    if(mp[{1, n}] && mp[{1, n - 1}] && mp[{2, n}])
    {
        if(x == 1 || y == n)
            cout << "YES\n";
        else
            cout << "NO\n";
        return;
    }
    if(mp[{n, 1}] && mp[{n, 2}] && mp[{n - 1, 1}])
    {
        if(x == n || y == 1)
            cout << "YES\n";
        else
            cout << "NO\n";
        return;
    }
    if(mp[{n, n}] && mp[{n, n - 1}] && mp[{n - 1, n}])
    {
        if(x == n || y == n)
            cout << "YES\n";
        else
            cout << "NO\n";
        return;
    }

    // 常规情况，平移L，如果目标点不在一个完整的区域中，可以先到达邻近的区域，再进行一至两步操作到达终点
    // 如果目标正好在2*2区域的孔雀位置，则无解
    int xx = a[1][0] + a[2][0] + a[3][0] - 2 * max({a[1][0], a[2][0], a[3][0]});
    int yy = a[1][1] + a[2][1] + a[3][1] - 2 * max({a[1][1], a[2][1], a[3][1]});
    if((xx - x) % 2 == 0 && (yy - y) % 2 == 0)
        cout << "NO\n";
    else
        cout << "YES\n";
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cout << fixed;
    cout.precision(18);

    int t;
    cin >> t;
    while(t--)
    {
        solve();
    }
    return 0;
}