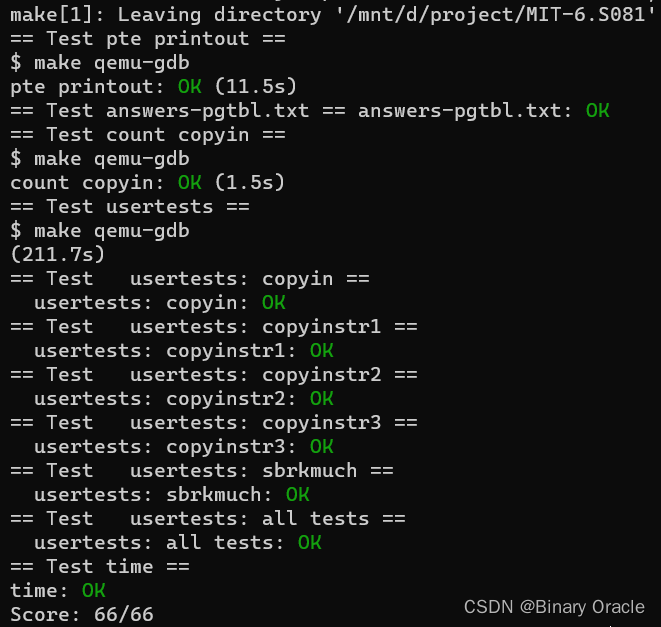
本文结合实例详细讲解了如何使用Python对栅格数据进行空间聚类，关注公众号GeodataAnalysis，回复20230616获取示例数据和代码，包含整体的写作思路，上手运行一下代码更容易弄懂。

带有非空间属性的空间数据聚类分析是空间聚类研究的热点和难点，聚类结果的应用领域很广，典型的就比如公众号之前介绍过的地理探测器¹。

地理探测器擅长自变量为类型量、因变量为数值量的分析，当自变量为数值量时，要采用一定的离散化方法将其转化为类型量。但很多影响因子是空间上连续分布的数值型变量，既具有地理域上的连续性，又具有属性域上的相似性。因此在聚类方法的选择上不仅要考虑属性特征的相似性，还要考虑对象的空间邻近性。坐标与属性一体化的空间聚类方法在对空间对象进行空间相似性度量时，将属性特征和地理位置特征同时纳入到距离测度中，以提高空间聚类分析的质量。

本文介绍的ACA-Cluster方法²基于一体化法进行改进，一体化法是将空间要素的位置（即坐标）和非空间属性数据都视为空间要素的属性数据，并使用属性距离函数计算相似度，再结合k-means算法进行聚类的方法。

1 相似度距离定义

聚类分析中常用的距离有近１０种，最常采用的距离之一曼哈顿距离。

假设任意两个空间对象 $P_i$ 、 $P_j$ 的中心坐标分别为 $x_i \, y_i)$ 和 $x_j \, y_j)$ ； $a_{ik}$ 和 $a_{jk}$ 分别是 $P_i$ 和 $P_j$ 上的值第k维度的属性值，则对象 $P_i$ 和 $P_j$ 之间的位置曼哈顿距离（ $D_p$ ）和属性曼哈顿距离（ $D_a$ ）可分别表示为：
$D_p = \frac{\lvert x_i - x_j \rvert + \lvert y_i - y_j \rvert}{2} \\ D_a = \frac{1}{M} \sum_{k=1}^M \lvert a_ik - a_jk \rvert$

其中， $D_p$ 表示位置距离，用以表达地物之间的邻近程度； $D_a$ 表示属性距离，用以刻画地物之间属性特征的相似性。此外，采用归一化方法去除位置距离和属性距离之间的单位限制。位置距离可以表达地物之间的邻近程度，属性距离则刻画地物之间属性特征的相似性。在聚类分析中，一般要求同类的地物既要在空间上邻近，又要在属性特征上相似。由此可见，单独采用位置距离或属性距离作为聚类分析的尺度，均不能很好地满足这一要求。为此，作者定义3种把位置距离和属性距离结合在一起的空间距离。

第一种定义方法是把空间坐标和属性特征同等对待：

$D_s = D_p + D_a$

第二种定义方法是对位置距离和属性距离进行加权，分别为 $w_p$ 和 $w_a$ ：

$D_s = w_p \cdot D_p + w_a \cdot D_a$

事实上，坐标中的两个坐标值对聚类分析的作用可能是不同的，其重要性用向量 $W(p) = (w_x, w_y)$ 表示；同样，属性特征集中的m个特征对聚类分析的作用也可能是不一样的，其重要性可用权重向量 $(w_1, w_2, w_3, \dots, w_m)$ 来表示，于是有了不等加权空间距离：

$D_a = w_x \cdot \lvert x_i - x_j \rvert + w_y \cdot \lvert y_i - y_j \rvert + \frac{1}{M} \sum_{k=1}^M w_k \cdot \lvert a_ik - a_jk \rvert$

2 基于空间位置和属性特点的空间聚类算法

算法实现：ACA-Cluster

输入：簇的数目k和包含ｎ个样品的数据集

输出：k个类别的矩阵

计算步骤：

设置最大迭代次数iternum。
随机取k个样品作为聚类中心。
计算其余样本到这k类的距离，将它们归为距离最近的类。至此，所有的样本都归类完毕。
计算各个类中心所有样品特征值的平均值作为该聚类中心的特征值。随着聚类中心的改变，样本的类号也在改变。
循环第３和第４步，直至不再有样本类号发生变化或达到了最大迭代次数。

3 代码实现

import numpy as np
import rasterio as rio
from osgeo import gdal
from sklearn_extra.cluster import KMedoids

class Cluster():

    def __init__(self, paths, std_method='feature') -> None:
        self.paths = paths
        self._check_data(self.paths)
        self._get_valid_coors()
        self.data = self._get_data()
        self._std(std_method)

    def _check_data(self, paths):
        '''检查所有数据文件是否横列数和空间范围全部相同，同时返回其行列数'''
        ds = gdal.Open(paths[0])
        RasterXSize, RasterYSize = ds.RasterXSize, ds.RasterYSize
        gt = ds.GetGeoTransform()
        proj = ds.GetProjection()
        for i in range(1, len(paths)):
            ds = gdal.Open(paths[i])
            assert RasterXSize == ds.RasterXSize
            assert RasterYSize == ds.RasterYSize
            assert gt == ds.GetGeoTransform()
            assert proj == ds.GetProjection()
    
    def _get_valid_coors(self):
        data = rio.open(self.paths[0])
        nodata = data.nodata
        array = data.read(1).astype(np.float32)
        array[array==nodata] = np.NAN
        coors = np.where(~np.isnan(array))
        self.coors_x, self.coors_y = coors[0], coors[1]
        self.input_shape = array.shape

    def _get_data(self):
        data = np.zeros((self.coors_x.size, len(self.paths)+2), dtype=np.float32)
        for i, path in enumerate(self.paths):
            src = rio.open(path)
            array = src.read(1)
            data[:, i] = array[self.coors_x, self.coors_y]
        data[:, -2] = self.coors_x
        data[:, -1] = self.coors_y
        return data

    def _std(self, mode):
        if 'feature' == mode:
            self.data =  (self.data-np.min(self.data, axis=0))/(np.max(self.data, axis=0)-np.min(self.data, axis=0))
        elif 'mean' == mode:
            self.data =  (self.data-np.mean(self.data, axis=0))/np.std(self.data, axis=0)
        else:
            raise ValueError

    def _geo_distance(self, x, y):
        a1, a2 = x[:-2], y[:-2]
        d1, d2 = x[-2:], y[-2:]

        d_p = np.abs(d1-d2) * self.w_p
        d_p = np.mean(d_p)

        d_a = np.abs(a1-a2) * self.w_a
        d_a = np.mean(d_a)

        return d_p + d_a

    def cluster(self, centerNum, max_iter=300, w_p=1, w_a=1):
        self.centerNum = centerNum
        self.w_p = np.array(w_p)
        self.w_a = np.array(w_a)
        kmedoids_custom = KMedoids(n_clusters=centerNum, metric=self._geo_distance, max_iter=max_iter)
        self.k = kmedoids_custom.fit(self.data)

        matrix = np.zeros(self.input_shape, dtype=np.int32)
        matrix[self.coors_x, self.coors_y] = self.k.labels_+1
        return matrix

4 实战演示

实验数据为分辨率为0.25度的降雨栅格数据，2014-2017年。

4.1 一维数据聚类

import numpy as np
from glob import glob
import rasterio as rio
from cluster import Cluster
import matplotlib.pyplot as plt

# 对2014年的降雨数据进行聚类
paths = [r'./pre/y2014.tif']
cluster = Cluster(paths, std_method='mean')

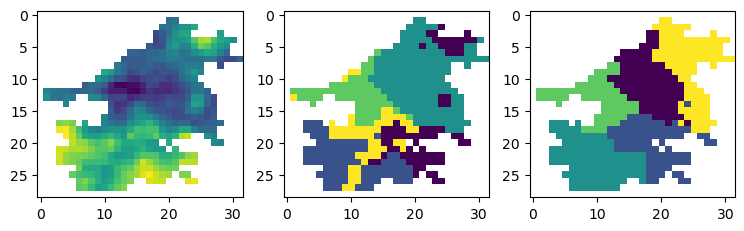
# 展示降雨数据
src = rio.open('./pre/y2014.tif')
pre = src.read(1)
pre = np.ma.masked_array(pre, mask=pre==src.nodata)

cluster_array1 = cluster.cluster(5, w_p=1, w_a=1)
cluster_array1 = np.ma.masked_array(cluster_array1, mask=cluster_array1==0)
cluster_array2 = cluster.cluster(5, w_p=2, w_a=1)
cluster_array2 = np.ma.masked_array(cluster_array2, mask=cluster_array2==0)

fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(9, 4))
ax1.imshow(pre)
ax2.imshow(cluster_array1)
ax3.imshow(cluster_array2);

最左侧为2014年的降雨数据，右侧的两个分别为按照第一种和第二种距离定义的聚类结果。

4.2 二维数据聚类

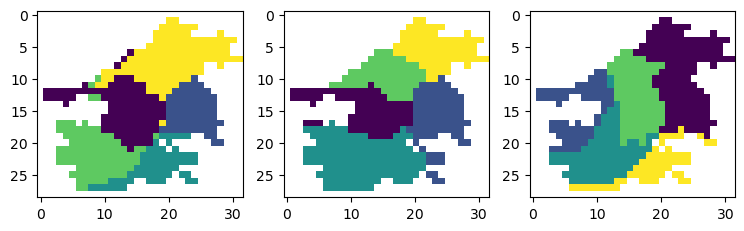
# 读取四年的降雨数据
paths = glob(r'./pre/*.tif')
cluster = Cluster(paths, std_method='mean')
cluster_array = cluster.cluster(5)

cluster_array1 = cluster.cluster(5, w_p=1, w_a=1)
cluster_array1 = np.ma.masked_array(cluster_array1, mask=cluster_array1==0)
cluster_array2 = cluster.cluster(5, w_p=2, w_a=1)
cluster_array2 = np.ma.masked_array(cluster_array2, mask=cluster_array2==0)
cluster_array3 = cluster.cluster(5, w_p=[1, 2], w_a=[1, 1, 2, 3])
cluster_array3 = np.ma.masked_array(cluster_array3, mask=cluster_array3==0)

fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(9, 4))
ax1.imshow(cluster_array1)
ax2.imshow(cluster_array2)
ax3.imshow(cluster_array3);

三个图分别为三种不同距离定义的聚类结果。

4.3 保存聚类结果

# numpy数组转tif
def array_to_tif(out_path, arr, crs, transform, nodata=None):
    # 获取数组的形状
    if arr.ndim==2:
        count = 1
        height, width = arr.shape
    elif arr.ndim==3:
        count = arr.shape[0]
        _, height, width = arr.shape
    else:
        raise ValueError
    
    with rio.open(out_path, 'w', 
                  driver='GTiff', 
                  height=height, width=width, 
                  count=count, 
                  dtype=arr.dtype, 
                  crs=crs, 
                  transform=transform, 
                  nodata=nodata) as dst:
        # 写入数据到输出文件
        if count==1:
            dst.write(arr, 1)
        else:
            for i in range(count):
                dst.write(arr[i, ...], i+1)

array_to_tif('./cluster.tif', cluster_array3.data, src.crs, src.transform, nodata=0)

参考文献：

[1]: 石亚冰，黄予。一种基于位置距离和属性特征结合的聚类方法。软件导刊，2013，12(3): 51-54.

[2]: Junwu Dong, Pengfei Liu, et al. Effects of anthropogenic precursor emissions and meteorological conditions on PM2.5 concentrations over the “2+26” cities of northern China. Environmental Pollution, 2022, 315: 120392.