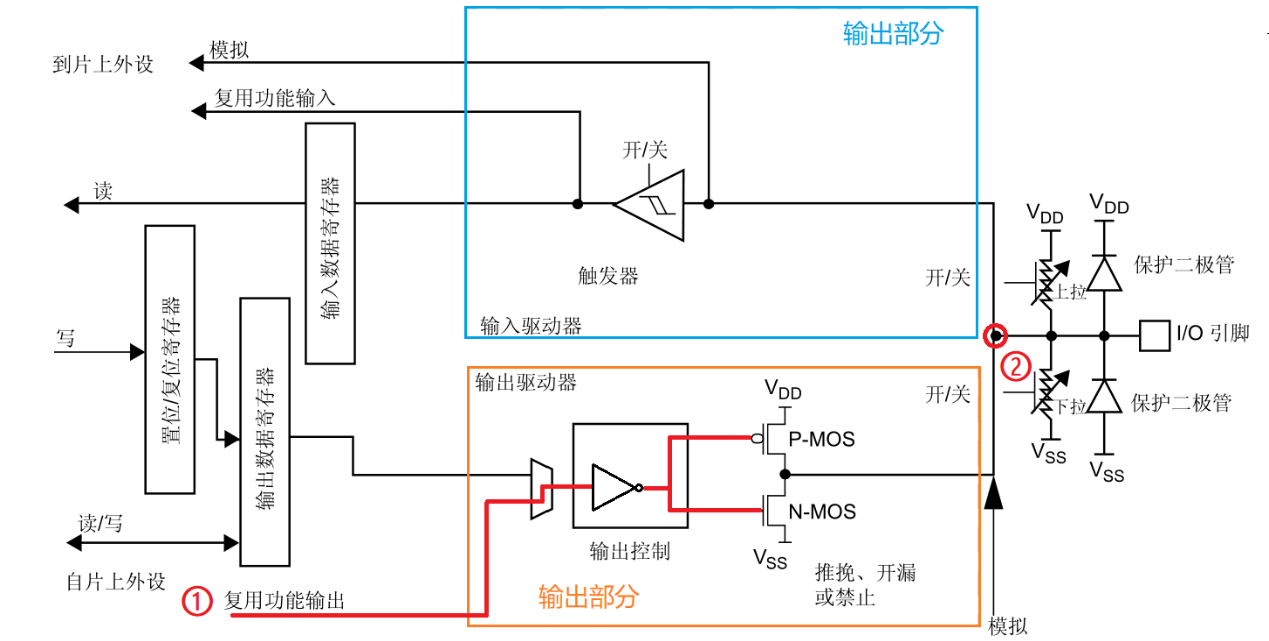
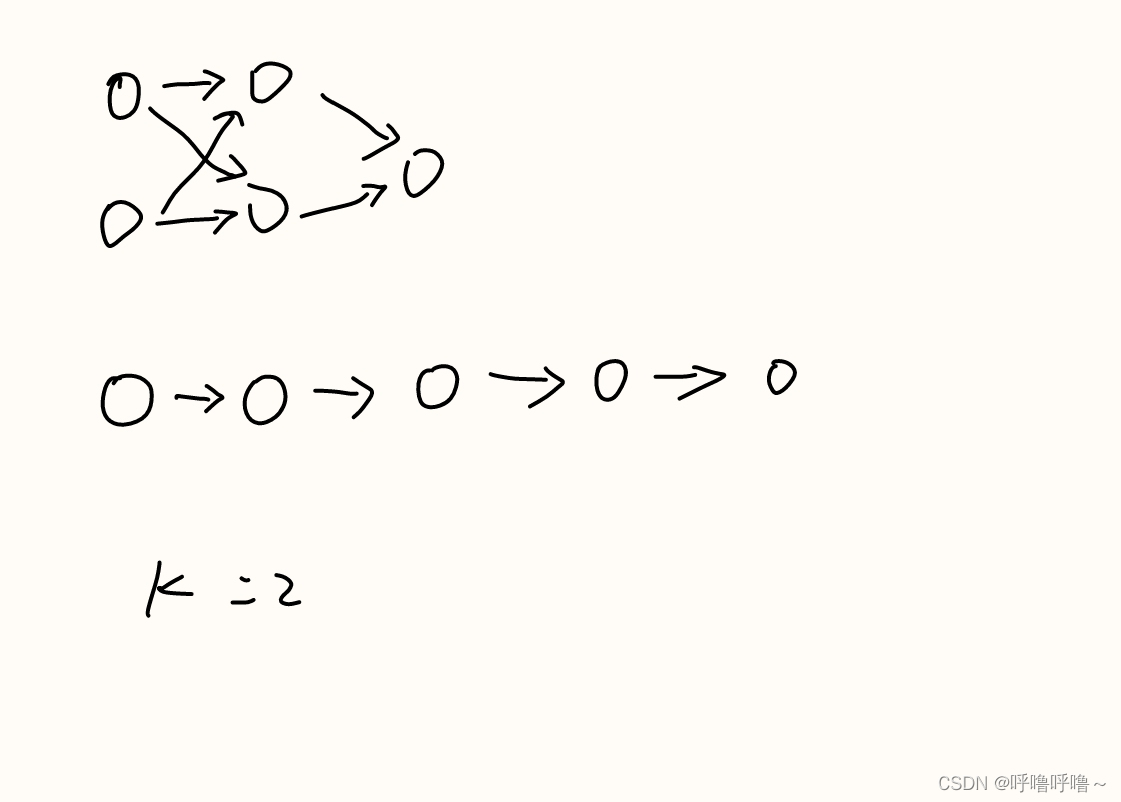【备战秋招】每日一题:4月23日美团春招第二题:题面+题目思路 + C++/python/js/Go/java带注释

news2024/11/17 1:34:49

为了更好的阅读体检，为了更好的阅读体检，，可以查看我的算法学习博客第二题-制作骰子

在线评测链接:P1246

题目内容

塔子哥是一个喜欢手工制作的人，他经常用各种材料制作一些有趣的物品。他最近想要制作一个骰子，但是他不想用普通的六面骰子，他想要制作一个更有挑战性的骰子。他想要制作一个总共有 n 面的骰子，而且每一面的数字也不同于普通的骰子，这 n 面的数字分别是 $a_1$ , $a_2$ ,…, $a_n$ 。

塔子哥知道，要制作一个合法的骰子，必须满足一个条件：所有相对的两面之和都需要相等。比如，如果一个骰子有六个面，分别是 1,2,3,4,2,3 ，那么可以把它摆成这样：上面是 1 ，下面是 4 ，前面是 2 ，后面是 3 ，左边是 2 ，右边是 3 。这样就满足了条件，因为相对的两面之和都是 5 。但是，如果一个骰子有六个面，分别是 1,2,4,5,6,7 ，那么就无法摆成合法的骰子，因为无论怎么摆，都会有相对的两面之和不相等。

塔子哥想要知道，给定 n 和 $a_1$ , $a_2$ ,..., $a_n$ ，能否制作出一个合法的骰子。他会给你总共若干次询问，每次询问他会告诉你 n 和 $a_1$ , $a_2$ ,..., $a_n$ 的值。你需要帮助塔子哥判断，在每次询问中，他是否能够制作出一个合法的骰子。

特别的，你不需要考虑只有 2 面或者只有 4 面的骰子是如何拼出来的，这方面塔子哥自然会解决，也就是说不需要从几何意义上考虑骰子面数是否满足条件。

输入描述

输入第一行为一个整数 T( $1 \leq T \leq 100$ ) ，表述询问数据的组数。

对于每组询问：

输入第一行为一个正整数 n( $1 \leq n \leq 100000$ ) ,表示骰子的面数，保证为偶数。

接下来输入一行为 n 个整数，分别为 a_1,a_2,...,a_n(1 \leq a_i \leq 1e6) 。

输出描述

对于每组询问，输出 Yes 或者 No 表示能否拼成骰子

样例1

输入

2
6
1 2 3 4 2 3
6
1 2 4 5 6 7

输出

Yes
No

样例2

输入

4
10
2 3 4 4 3 3 2 1 1 2
20
3 1 3 3 3 4 3 2 1 4 1 1 3 1 1 3 4 4 2 2
18
4 2 1 4 2 3 2 4 2 1 3 4 1 3 2 3 1 3
4
4 2 3 2

输出

Yes
No
Yes
No

思路

简化题意

给定一个长度为 n 的数组，每两个数一组，是否可以使得每组的和都相同？

这里为了方便描述，假设每个数都不一样，且 $a_1$ < $a_2<a_3<\cdots<a_n$

观察

容易看出来的是：最小值a_1 和最大值 a_n 必须一组

证明

反证法,如果 $a_1$ 不和 $a_n$ 一组，则 $a_1$ 和 $a_j$ (1<j<n) 一组， $a_k(1<k<n,k\neq j)$ 和 $a_n$ 一组。首先有 $a_k>a_1$ ，再者有 $a_n>a_j$ ，故 $a_n+a_k>a_1+a_j$ 。此时无论怎么分组，都有至少这两组的和不同。

下一步

这显然成为一个子问题。即 $a_2$ 到 $a_{n-1}$ 这 n-2 个数分成两两一组，使得各组之和相同。同样是 $a_{2}$ 和 $a_{n-1}$ 必须一组。

故最后的分组为： $(a_1,a_n),(a_2,a_{n-1}),\cdots,(a_{n/2},a_{n/2+1})$ 。然后判断各组之和是否都相等即可。

时间复杂度：O(n\log n)，排序的复杂度

类似题目推荐

这是比较简单的贪心题。

Leetcode

LeetCode上的贪心题，代码随想录总结的非常好了，见贪心 - 代码随想录

Codefun2000

美团还是挺喜欢考贪心的，但是大部分是简单贪心吧，如下所示 , 可以过一遍

P1137 美团 2023.04.01-第一题-整理
P1077 美团 2023.3.11-第一题-字符串修改
P1024 百度 2022.9.13-01反转
P1235. 美团 2023.04.15-实习-第一题-字符串前缀
P1089 美团 2023.3.18.10点-第三题-塔子哥的回文串

代码

CPP

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;
int a[N], n;
void solve() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
    sort(a + 1, a + n + 1);
    // 最大最小必须在同一组
    int sum = a[1] + a[n];
    bool ok = true;
    // 子问题，往内收缩，比较
    int l = 2, r = n - 1;
    while (l < r) {
        if (a[l] + a[r] != sum) {
            ok = false;
            break;
        }
        l += 1;
        r -= 1;
    }

    puts(ok ? "Yes" : "No");
}

int main()
{
    int T = 1;
    scanf("%d", &T);
    while (T--) {
        solve();
    }

    return 0;
}

Java

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static final int N = 100010;
    static int[] a = new int[N];
    static int n;

    private static Scanner sc = new Scanner(System.in);


    public static void solve() {
        n = sc.nextInt();
        for (int i = 1; i <= n; ++i) a[i] = sc.nextInt();
        Arrays.sort(a, 1, n + 1);
        // 最大最小必须在同一组
        int sum = a[1] + a[n];
        boolean ok = true;
        int l = 2, r = n - 1;
        // 子问题，往内收缩，比较
        while (l < r) {
            if (a[l] + a[r] != sum) {
                ok = false;
                break;
            }
            l += 1;
            r -= 1;
        }

        System.out.println(ok ? "Yes" : "No");
    }

    public static void main(String[] args) {
        int T = 1;
        T = sc.nextInt();
        while (T-- > 0) {
            solve();
        }
    }
}

Python

N = 100010
a = [0] * N
n = 0


def solve():
    global a, n
    n = int(input())
    a = list(map(int, input().split()))
    a.sort()
    # 最大最小必须在同一组
    sum_ = a[0] + a[-1]
    ok = True
    l, r = 1, n - 2
    # 子问题，往内收缩，比较
    while l < r:
        if a[l] + a[r] != sum_:
            ok = False
            break
        l += 1
        r -= 1

    print('Yes' if ok else 'No')


T = int(input())
while T:
    solve()
    T -= 1

Go

package main

import (
    "fmt"
    "sort"
)

var (
    N = 100010
    a = make([]int, N)
    n int
)

func solve() {
    nScan, _ := fmt.Scanln(&n)
    if nScan == 0 {
        return
    }

    for i := 0; i < n; i++ {
        fmt.Scan(&a[i])
    }
    sort.Ints(a[:n])

    // 最大最小必须在同一组
    sum_ := a[0] + a[n-1]
    ok := true
    l, r := 1, n-2
    // 子问题，往内收缩，比较
    for l < r {
        if a[l]+a[r] != sum_ {
            ok = false
            break
        }
        l++
        r--
    }

    if ok {
        fmt.Println("Yes")
    } else {
        fmt.Println("No")
    }
}

func main() {
    var T int
    fmt.Scanln(&T)
    for T > 0 {
        solve()
        T--
    }
}

Js

process.stdin.resume();
process.stdin.setEncoding('utf-8');
let input = '';
process.stdin.on('data', (data) => {
    input += data;
    return;
});

process.stdin.on('end', () => {
    const lines = input.trim().split('\n');
    let [T, ...testCases] = lines;

    function solve(a) {
        a.sort((a, b) => a - b);
        const n = a.length;

        // 最大最小必须在同一组
        const sum = a[0] + a[n - 1];
        let ok = true;
        let l = 1, r = n - 2;

        // 子问题，往内收缩，比较
        while (l < r) {
            if (a[l] + a[r] != sum) {
                ok = false;
                break;
            }
            l++;
            r--;
        }

        console.log(ok ? "Yes" : "No");
    }

    for (let i = 0; i < T; i++) {
        const n = Number(testCases[i * 2]);
        const a = testCases[i * 2 + 1].split(" ").map(Number);
        solve(a);
    }
});

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/655221.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！