[ 目录 ]
- 0. 前言
- 1. 耳切法
- (1)基础的概念
- (2)耳点判断
- (3)判断角度类型
- (4)点是否在三角形内
- (5)判断顺逆时针
- 2. 耳切法小优化
- 3. 耳切法实现
- (1)基础定义
- (2)实现
- 4. 测试
- 5. 结束咯
0. 前言
有个小需求是分割一下多边形,顺带记录一下。通常来说多边形的形状都比较复杂,不好进行操作,这个时候如果我们可以把一个多边形分隔为若干个三角形,回归到简单基础的形状就方便我们操作。三角形化在渲染显示中还是挺多用的。下文未列出,但涉及到的代码链接如下。
链接:https://pan.baidu.com/s/1kl7kwksYMHn3YerpimvL3w?pwd=wsad
提取码:wsad
1. 耳切法
(1)基础的概念
先了解一下耳切法的基础概念。
- 耳切法: 耳点在简单多边形中是一个凸顶点,将该点移除之后,多边形边数减少1,重复改过程,最终完成三角化。
- 耳点: 多边形顶点相邻两个点连成一条线段,这条线段完全落在这个多边形的内部。
- 简单多边形: 几何学中将互不相交的线段成对连接形成的闭合路径的平面图形。
所以我们可以发现使用耳切法就是重复找耳点删耳点这个过程,如下。
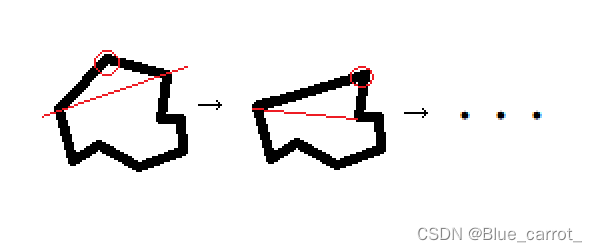
那我们的问题就变换成了如何去判断这个耳点
(2)耳点判断
那耳点怎么找呢,这个可以分解为两个条件。
- 突出的点,和两边的点的夹角需要小于180度
- 和两边的点组成的三角形内不包含多边形内的其他点
其实看图也比较好理解,下图中0就是满足两个条件的耳点,而1,2分别是不满足这个两个条件的非耳点
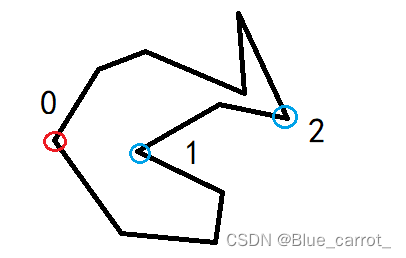
(3)判断角度类型
判断耳点条件的话,可以通过两个向量的叉乘外积的方式来判断
//OA和OB的角在180度一下
private bool IsAngleLessThan180(Vector3 o,Vector3 a,Vector3 b)
{
return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x) > 0;
}
这里有一个要注意的是,那一边才是多边形的里面。如果是多边形按顺时针排序点的话的话,就可以如上判断,但如果是逆时针的话其实是相反的。分别是顺、逆时针的图。后面我们再讲下如何判断多边形给的角的旋转角度。
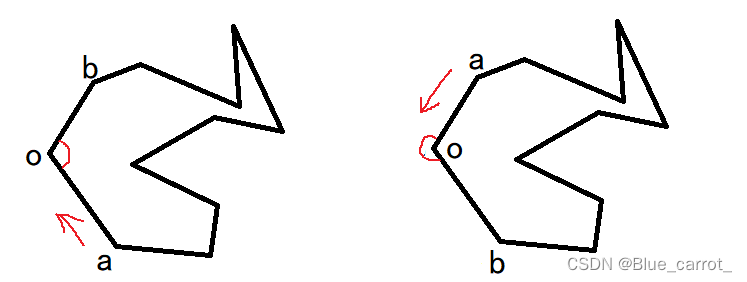
(4)点是否在三角形内
这里通过向量叉乘来判断点是否在线的左边或者右边,然后3条边对于这个点p都应该在同一边的话,说明点在三角形内,如果不是则说明在三角形内。
private bool IsContain(Vector3 a, Vector3 b, Vector3 c, Vector3 p)
{
var c1 = (b.x - a.x) * (p.y - b.y) - (b.y - a.y) * (p.x - b.x);
var c2 = (c.x - b.x) * (p.y - c.y) - (c.y - b.y) * (p.x - c.x);
var c3 = (a.x - c.x) * (p.y - a.y) - (a.y - c.y) * (p.x - a.x);
return c1 > 0f && c2 > 0f && c3 > 0f || c1 < 0f && c2 < 0f && c3 < 0f;
}
(5)判断顺逆时针
去判断顺逆时针的话也是计算叉乘的方式,至于为什么这样就能判断顺逆时针,有点类似于(3)。
private bool IsClockWise(Vector2[] points)
{
// 通过计算叉乘来确定方向
float sum = 0f;
double count = points.Length;
Vector3 va, vb;
for (int i = 0; i < points.Length; i++)
{
va = points[i];
vb = (i == count - 1) ? points[0] : points[i + 1];
sum += va.x * vb.y - va.y * vb.x;
}
return sum < 0;
}
好咯,所有的条件都已经去判断了,耳切法就可以去实现了。
2. 耳切法小优化
通过1,我们已经实现了耳切法,但是有特殊情况,比如多边形如下
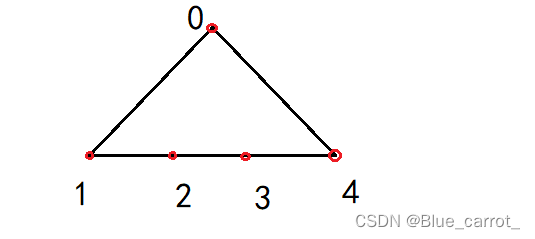
1234点在同一个直线,那么当0被判断为耳点并移除之后,其他的点在同一条直线上无法组成三角形的。虽然也没有关系,因为三角形也分隔完了,但这样就会有多余的点留,剩下的点也无法判断为是耳点。我们尽量让所有点都可以被界定,除非是非简单多边形。
所以我们先做一个小调整,就判断内角的时候先判断是不是平角,如果是平角直接移除中间的点。这里我们先定义一下角度
enum AngleType
{
/// <summary>
/// 平角 = 180
/// </summary>
StraightAngle = 0,
/// <summary>
/// 优角 >180
/// </summary>
ReflexAngle = 1,
/// <summary>
/// 劣角 <180
/// </summary>
InferiorAngle = 2,
}
判断角度的函数 IsAngleLessThan18,重新调整一下, 另外加入我们之前考虑过的顺逆时针的条件,那么可以调整为
/// <summary>
/// 判断角的类型,oa & ob 之间的夹角,(右手法则)
/// </summary>
private AngleType GetAngleType(Vector2 o, Vector2 a, Vector2 b, bool isClockWise)
{
float f = (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x);
bool flag = isClockWise ? f > 0 : f < 0;
if (f == 0)
{
return AngleType.StraightAngle;
}
else if (flag)
{
return AngleType.InferiorAngle;
}
else
{
return AngleType.ReflexAngle;
}
}
3. 耳切法实现
(1)基础定义
先定义三角形Triangle,多边形Polygon两个结构体。
public struct Triangle
{
public Vector2 a;
public Vector2 b;
public Vector2 c;
}
public struct Polygon
{
public Vector2[] points;
}
此外,考虑到多边形是一个环形,而且我们要频繁的去移除这些点,所以用一个双向链表的结构来处理会更好。C#也有提供了,但也不是很方便,因为多边形还要首尾相连会更合适。我们自己先定义一下这个节点
public class PointNode
{
public Vector2 Position;
public PointNode PreviousNode;
public PointNode NextNode;
public PointNode(Vector2 Position)
{
this.Position = Position;
}
}
(2)实现
前面的把流程都说完好了,这里就单纯发一下函数把。
/// <summary>
/// 三角形化
/// </summary>
/// <returns></returns>
public Triangle[] Triangulate()
{
if (points.Length < 3)
{
return new Triangle[0];
}
else
{
// 节点数量
int count = points.Length;
// 确定方向
bool isClockWise = IsClockWise();
// 初始化节点
PointNode curNode = GenPointNote();
// 三角形数量
int triangleCount = count - 2;
// 获取三角形
List<Triangle> triangles = new List<Triangle>();
AngleType angleType;
while (triangles.Count < triangleCount)
{
// 获取耳点
int i = 0, maxI = count - 1;
for (; i <= maxI; i++)
{
angleType = GetAngleType(curNode, isClockWise);
if (angleType == AngleType.StraightAngle)
{
// 等于180,不可能为耳点
// 移除当前点,三角形数量少一个
curNode = RemovePoint(curNode);
count--;
triangleCount--;
}
else if (angleType == AngleType.ReflexAngle)
{
// 大于180,不可能为耳点
curNode = curNode.NextNode;
}
else if (IsInsideOtherPoint(curNode, count))
{
//包含其他点,不可能为耳点
curNode = curNode.NextNode;
}
else
{
// 当前点就是ear,添加三角形,移除当前节点
triangles.Add(GenTriangle(curNode));
curNode = RemovePoint(curNode);
count--;
break;
}
}
// 找不到ear
if (i > maxI)
{
triangles.Clear();
break;
}
}
return triangles.ToArray();
}
}
4. 测试
写一个简单的脚本来测试一下效果,下面脚本的作用是鼠标点击然后绘点,再用耳切法分隔,并画出图形
using System.Collections;
using System.Collections.Generic;
using GDT;
using GenericShape;
using UnityEngine;
public class TestPMono : MonoBehaviour
{
public List<Vector2> points;
public Triangle[] triangles;
// Start is called before the first frame update
void Start()
{
points = new List<Vector2>();
// points.Add(new Vector2(0, 100));
// points.Add(new Vector2(0, 200));
// points.Add(new Vector2(0, 300));
// points.Add(new Vector2(200, 200));
// points.Add(new Vector2(0, 0));
PolygonNode node = new PolygonNode(points.ToArray());
triangles = node.Triangulate();
Debug.Log("triangles:" + triangles.Length);
}
void OnMouseDown()
{
points.Add(Input.mousePosition);
if (points.Count > 3)
{
PolygonNode node = new PolygonNode(points.ToArray());
triangles = node.Triangulate();
}
}
// Update is called once per frame
void Update()
{
// 画多边形
DebugUtil.DrawPolygon(points, Color.red);
for (int i = 0; i < points.Count; i++)
{
DebugUtil.DrawCricle(points[i], 8, 0.1f, Color.red);
}
// 画三角形
if (triangles != null)
{
for (int i = 0; i < triangles.Length; i++)
{
DebugUtil.DrawTriangle(
triangles[i].a, triangles[i].b, triangles[i].c, Color.red);
}
}
}
}
画图形的 DebugUtil.DrawTriangle等如下,后面如果有机会,再整理一下这种调试用的Draw吧
public static void DrawTriangle(Vector2 a, Vector2 b, Vector2 c, Color color, float duration = 0)
{
Debug.DrawLine(a, b, color, duration);
Debug.DrawLine(b, c, color, duration);
Debug.DrawLine(c, a, color, duration);
}
public static void DrawCricle(Vector2 center, float radius, float thetaDelta, Color color, float duration = 0)
{
float thetaMax = Mathf.PI * 2;
Vector2 first = new Vector2(radius, 0) + center;
Vector2 a = first, b;
for (float theta = 0; theta < thetaMax; theta += thetaDelta)
{
b = a;
a.y = radius * Mathf.Sin(theta);
a.x = radius * Mathf.Cos(theta);
a += center;
Debug.DrawLine(a, b, color, duration);
}
Debug.DrawLine(first, a, color, duration);
}
public static void DrawPolygon(Vector2[] points, Color color, float duration = 0)
{
if (points.Length > 0)
{
for (int i = 1; i < points.Length; i++)
{
Debug.DrawLine(points[i - 1], points[i], color, duration);
}
Debug.DrawLine(points[0], points[points.Length - 1], color, duration);
}
}
public static void DrawPolygon(List<Vector2> points, Color color, float duration = 0)
{
if (points.Count > 0)
{
for (int i = 1; i < points.Count; i++)
{
Debug.DrawLine(points[i - 1], points[i], color, duration);
}
Debug.DrawLine(points[0], points[points.Count - 1], color, duration);
}
}
简单测试一下。
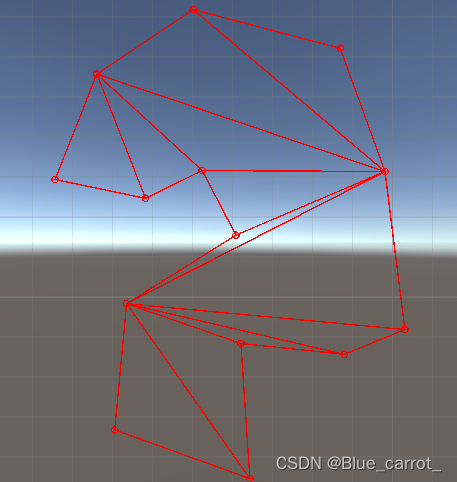
好耶,没什么问题,终于写完了…。
5. 结束咯
终于写完了…之后估计会考虑一下非简单多边形怎么处理,比如有两线交叉的情况。第二个情况是多边形中间有岛洞的情况,这两种情况后续有时间再考虑吧。没时间处理了。
相关参考文献
耳切法(应该是原论文)
https://www.geometrictools.com/Documentation/TriangulationByEarClipping.pdf
耳切实现(虽然是日文的,但有图例,写的很清楚,非常推荐)
https://qiita.com/fujii-kotaro/items/a411f2a45627ed2f156e
其他介绍
https://blog.csdn.net/u010019717/article/details/52753855/
https://blog.csdn.net/THUNDERDREAMER_OR/article/details/104184589