练习:有限状态机测试
1 FSM 示例
在练习中,我们将使用两个 FSM。 两者都有输入字母 X = {a, b} 和输出字母 Y = {0,1}。 第一个 FSM 将称为 M1 并由以下有向图表示。
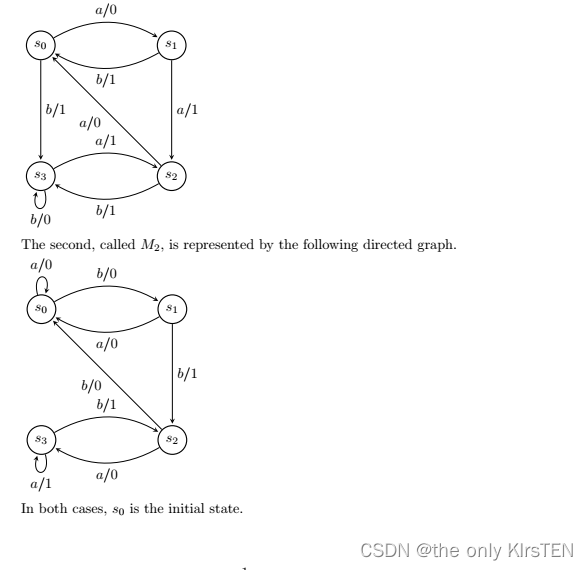
对于上面给出的每个 FSM Mi:
1.确定以下值,显示您的工作。
(a) δ*(s0, abbab)。
(b) λ*(s0, abbab)。
δ is a state transfer function of type S x X ->S
λ is a output function of type S x X ->Y
For M1, so (a) is {s1,s0,s3,s2,s3} and (b) is abbab
For M2, so (a) is {s0,s1,s2,s3,s2} and (b) is abbab
2.对于 Mi 的每个状态 s,找到一个使 Mi 从其初始状态到状态 s 的输入序列。 在每种情况下,确定这是否是最短的此类输入序列。
For M1:
to s1,(s0,s1,a/0)
to s2,(s0,s1,a/0) (s1,s2,a/1)
to s3,(s0,s3,b/1)
For M2:
to s1,(s0,s1,b/0)
to s2,(s0,s1,b/0) (s1,s2,b/1)
to s3, (s0,s1,b/0) (s1,s2,b/1) (s2,s3,a/0)
3.导出过渡游。
For M1,
(s0,s3,b/1) (s3,s3,b/0) (s3,s2,a/1) (s2,s0,a/0) (s0,s1,a/0) (s1,s0,b/1) (s0,s1,a/0) (s1,s2,a/1) (s2,s3,b/1)
For M2,
(s0,s0,a/0) (s0,s1, b/0) (s1,s0,a/0) (s0,s1, b/0) (s1,s2,b/1) (s2, s3,a/0) (s3,s3,a/1) (s3,s2,b/1) (s2,s0,b/0)
4.评论这是否是最短的过渡游。 如果不是,则生成最短的过渡行程。
yes it is


3 FSM 示例
相同的 M1 和 M2
对于上面给出的每个 FSM Mi:
- 判断Mi的每个状态是否有UIO。
- 哪里有一个状态的UIO,就找到这样一个UIO。
- 为 Mi 找到一个特征集。
- 应用 W 方法(无额外状态)。
For M1
在示例中,b/0 为状态 s3 形成一个 UIO:
从状态 s0 输出序列为 1
从状态 s1 输出序列为 1
从状态 s2 输出序列为 1
从状态 s3 输出序列为 0
because s3 has UIO so that in order to go to s3 so that
t = (s0,s3,b/1)
so through b could go to
| state | aa |
|---|---|
| s0 | 01 |
| s1 | 10 |
| s2 | 00 |
| s3 | 10 |
| state | ab |
|---|---|
| s0 | 01 |
| s1 | 11 |
| s2 | 01 |
| s3 | 00 |
V is {empty,a,aa,b)
W IS {aa,ab}
X is {a,b}
Answers:

if there did not give the m, then we normally consider m = n so that is V W U V X W
if m = n+1, then
V W U V X W U V XX W
and the reason it only therefore obtain V X W is because it automatically included V W
For M2
在示例中,a/1 为状态 s3 形成一个 UIO:
从状态 s0 输出序列为 0
从状态 s1 输出序列为 0
从状态 s2 输出序列为 0
从状态 s3 输出序列为 1
and b/0 did not have because s0 and s2 would produce that
and b/1 not have because s3 and s1 have so that
only s3 has a UIO and s0,s1,s2 did not have.
because s3 has UIO so that in order to go to s3 so that
t = (s0,s1,b/0) (s1,s2,b/1) (s2,s3,a/0)
so through bba could go to
| state | b |
|---|---|
| s0 | 0 |
| s1 | 1 |
| s2 | 0 |
| s3 | 1 |
| state | ab |
|---|---|
| s0 | 00 |
| s1 | 00 |
| s2 | 01 |
| s3 | 11 |
V is {empty, b,bb,bba}
W is {b,ab}
X is {a,b}
![[MySQL]不就是SQL语句](https://img-blog.csdnimg.cn/b5811955fd124f52b3f8713ba33da5b6.png)