⭐️前言⭐️
动态规划是一个很难的模块,如果一道动态规划的题目直接去推出动态转移方程来解题,是很难的,所以应该先想出暴力解决的方法,再去用空间换时间优化,得出动态规划的解法。
🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁
🍉博主将持续更新学习记录收获,友友们有任何问题可以在评论区留言
🍉博客中涉及源码及博主日常练习代码均已上传GitHub

📍内容导读📍
- 🍅机器人走路
- 🍅拿牌游戏
🍅机器人走路
题目:
假设有排成一行的N个位置记为1~N,N一定大于或等于2
开始时机器人在其中的M位置上(M一定是1~N中的一个)
如果机器人来到1位置,那么下一步只能往右来到2位置;
如果机器人来到N位置,那么下一步只能往左来到N-1位置;
如果机器人来到中间位置,那么下一步可以往左走或者往右走;
规定机器人必须走K步,最终能来到P位置(P也是1~N中的一个)的方法有多少种
给定四个参数 N、M、K、P,返回方法数
题解思路1:
暴力递归,列举所有可能性,确定结束递归的条件,把所有的可能性加起来就是结果。
代码实现:
public class RobotWalk {
/**
* @param N 有1~N个位置
* @param start 起始位置
* @param aim 目标位置
* @param k 要走k步
* @return
*/
public static int ways(int N,int start,int aim,int k) {
return process(start,k,aim,N);
}
/**
* @param cur 目前所在位置
* @param rest 剩余步数
* @param aim 目标位置
* @param N 有N个位置
* @return
*/
public static int process(int cur,int rest,int aim,int N) {
if(rest==0) {
return cur==aim?1:0;
}
if(cur==1) {
return process(2,rest-1,aim,N);
}
if(cur==N) {
return process(N-1,rest-1,aim,N);
}
return process(cur-1,rest-1,aim,N)+process(cur+1,rest-1,aim,N);
}
}
题解思路2:
记忆化搜索、从顶向下的动态规划
假设一开始在位置3,剩余4步,那么下一步可能走到位置2,剩余3步;或者位置4,剩余3步;这两个位置都能走到位置3,剩余2步,位置3到达aim的可能性只由该位置决定,与怎样到达位置3的没关系,所以为了减少重复计算,可以增加缓存表,把之前的结果记录下来,当后续其他分支又走到该位置时,可以直接使用不需要再计算。
代码实现:
public class RobotWalk {
public static int ways2(int N,int start,int aim,int k) {
int[][] dp=new int[N+1][k+1];
for (int i = 0; i <=N; i++) {
for (int j = 0; j <=k; j++) {
dp[i][j]=-1;
}
}
return process2(start,k,aim,N,dp);
}
public static int process2(int cur, int rest, int aim, int N, int[][] dp) {
if(dp[cur][rest]!=-1) {
return dp[cur][rest];
}
int ans=0;
if(rest==0) {
ans=cur==aim?1:0;
}else if(cur==1) {
ans=process2(2,rest-1,aim,N,dp);
}else if(cur==N) {
ans=process2(N-1,rest-1,aim,N,dp);
}else {
ans=process2(cur-1,rest-1,aim,N,dp)+process2(cur+1,rest-1,aim,N,dp);
}
dp[cur][rest]=ans;
return ans;
}
}
题解思路3:
动态规划最终版本,假设共有5个位置,2为起始位置,4为目标位置,需要走6步,那动态转移结果如下:
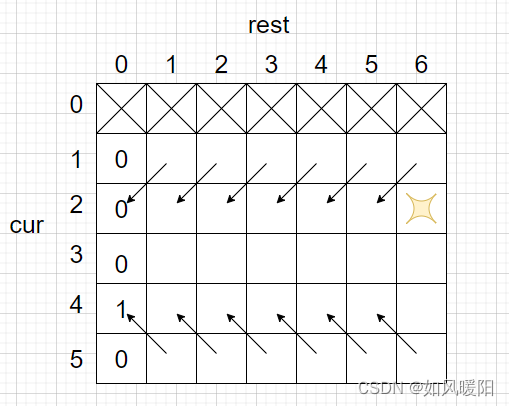
即求cur=2,rest=6位置的结果,cur=1时,结果依赖于与cur=2,rest-1位置的结果;
cur=5时,结果依赖于cur=4,rest-1位置的结果;中间位置的结果,依赖于(cur-1,rest-1)+(cur+1,rest-1)位置的结果。根据以上的规则,来完成dp表的填写,最终返回(2,6)位置的结果即可。
代码实现:
public class RobotWalk {
public static int ways3(int N,int start,int aim,int k) {
int[][] dp=new int[N+1][k+1];
dp[aim][0]=1;
for (int rest = 1; rest <=k ; rest++) {
dp[1][rest]=dp[2][rest-1];
for (int cur = 2; cur < N; cur++) {
dp[cur][rest]=dp[cur-1][rest-1]+dp[cur+1][rest-1];
}
dp[N][rest]=dp[N-1][rest-1];
}
return dp[start][k];
}
}
结果测试:

🍅拿牌游戏
题目:
给定一个整型数组arr,代表数值不同的纸牌排成一条线
玩家A和玩家B依次拿走每张纸牌
规定玩家A先拿,玩家B后拿
但是每个玩家每次只能拿走最左或最右的纸牌
玩家A和玩家B都绝顶聪明
请返回最后获胜者的分数
题解思路1:
拿牌有先手和后手两种姿态:
先手拿牌,所能拿到的最大分数为
1.arr[L]+后手在[L+1,R]范围取到的最小值(因为是后手所以取到的只能是最小值)
2.arr[R]+后手在[L,R-1]范围内取到的最小值
1、2中的最大值。
如果只剩一张牌,那就直接拿走。
后手拿牌,所能拿到的最大分数为
1.先手在[L+1,R]范围内的最大值
2.先手在[L,R-1]范围内的最大值
1、2中的最小值,因为为后手取牌,所以得到的结果肯定为较小的结果。
如果只剩一张牌,那么只能拿到0。
代码实现:
public class CardsInLine {
// 根据规则,返回获胜者的分数
public static int win1(int[] arr) {
if(arr==null||arr.length==0) {
return 0;
}
int first=f1(arr,0,arr.length-1);
int second=g1(arr,0,arr.length-1);
return Math.max(first,second);
}
// arr[L..R] 先手获得的最好分数返回
public static int f1(int[] arr, int L, int R) {
if(L==R) {
return arr[L];
}
int p1=arr[L]+g1(arr,L+1,R);
int p2=arr[R]+g1(arr,L,R-1);
return Math.max(p1,p2);
}
// arr[L..R] 后手获得的最好分数返回
public static int g1(int[] arr, int L, int R) {
if(L==R) {
return 0;
}
int p1=f1(arr,L+1,R); // 对手拿走了L位置的数
int p2=f1(arr,L,R-1); // 对手拿走了R位置的数
return Math.min(p1,p2);
}
}
题解思路2:
由下图的依赖关系可得,还是会有重复的计算,所以可以通过缓存来减少重复的计算。
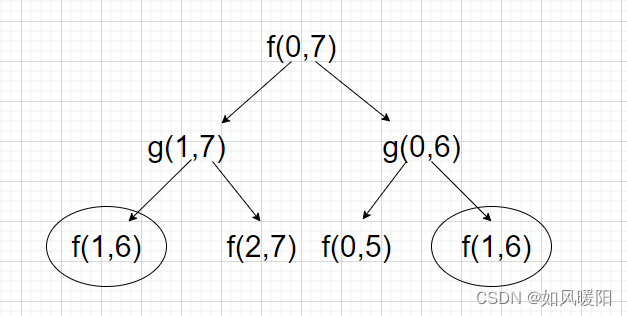
代码实现:
public class CardsInLine {
public static int win2(int[] arr) {
if(arr==null||arr.length==0) {
return 0;
}
int N= arr.length;
int[][] fmap=new int[N][N];
int[][] gmap=new int[N][N];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
fmap[i][j]=-1;
gmap[i][j]=-1;
}
}
int first=f2(arr,0,arr.length-1,fmap,gmap);
int second=g2(arr,0,arr.length-1,fmap,gmap);
return Math.max(first,second);
}
public static int f2(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {
if(fmap[L][R]!=-1) {
return fmap[L][R];
}
int ans=0;
if(L==R) {
ans=arr[L];
}else {
int p1=arr[L]+g2(arr,L+1,R,fmap,gmap);
int p2=arr[R]+g2(arr,L,R-1,fmap,gmap);
ans=Math.max(p1,p2);
}
fmap[L][R]=ans;
return ans;
}
public static int g2(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {
if(gmap[L][R]!=-1) {
return gmap[L][R];
}
int ans=0;
if(L!=R) {
int p1=f2(arr,L+1,R,fmap,gmap); // 对手拿走了L位置的数
int p2=f2(arr,L,R-1,fmap,gmap); // 对手拿走了R位置的数
ans=Math.min(p1,p2);
}
gmap[L][R]=ans;
return ans;
}
}
题解思路3:
状态转移表,根据暴力递归解法,来推断出表格中的结果。
假设一组数据为[7,4,16,15,1],那么对应的两张表的状态如下:
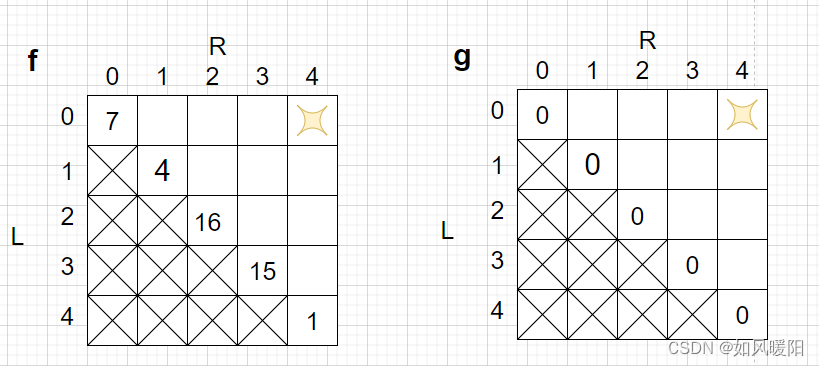
在f表中,如果L == R,即返回该位置的值,而在g表中,作为后手姿态,L==R时,只能获得0.
因为L<=R,所以表格中不合法区域直接用×排除
最终即判断f表中(0,4)与g表中(0,4)两个位置的结果大小,返回较大的即可。
其余位置的填写规则,可以由暴力递归的解法来得出。
比如g(0,1)位置,其结果依赖于f(1,1)与f(0,0)两个位置的结果;f(0,1)位置,其结果依赖于g(1,1)与g(0,0)两个位置的结果;即可得出规则,填写结果依赖于另一张表对应位置的左、下位置的结果。
代码实现:
public class CardsInLine {
public static int win3(int[] arr) {
if(arr==null||arr.length==0) {
return 0;
}
int N=arr.length;
int[][] fmap=new int[N][N];
int[][] gmap=new int[N][N];
for (int i = 0; i < N; i++) {
fmap[i][i]=arr[i];
}
for (int i = 1; i < N; i++) {
int L=0;
int R=i;
while (R<N) {
fmap[L][R]=Math.max(arr[L]+gmap[L-1][R],arr[R]+gmap[L][R-1]);
gmap[L][R]=Math.min(fmap[L-1][R],gmap[L][R-1]);
L++;
R++;
}
}
return Math.max(fmap[0][N-1],gmap[0][N-1]);
}
}
⭐️最后的话⭐️
总结不易,希望uu们不要吝啬你们的👍哟(^U^)ノ~YO!!如有问题,欢迎评论区批评指正😁