题目:
噪声过程由IID零均值,PDF为
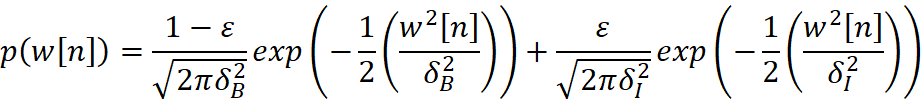
的随机变量组成,其中0<ε<1 。这样的PDF成为高斯混合PDF,它用来模拟![]() 具有方差为
具有方差为![]() 的高斯噪声以及剩余的服从方差
的高斯噪声以及剩余的服从方差![]() 的高斯噪声。一般
的高斯噪声。一般![]() ,且ε≪1 ,所以具有方差为
,且ε≪1 ,所以具有方差为![]() 的背景噪声在噪声中起主要作用。但是也包含高电平事件或者干扰,这是使用方差为
的背景噪声在噪声中起主要作用。但是也包含高电平事件或者干扰,这是使用方差为![]() 的高斯噪声来模拟的。证明这种PDF的方差为:
的高斯噪声来模拟的。证明这种PDF的方差为:
![]()
如果认为![]() 是数据,且
是数据,且![]() 假定已知,求
假定已知,求![]() 的BLUE。提示,利用习题6.12的结果。
的BLUE。提示,利用习题6.12的结果。
解答
1. 证明
已知随机变量![]() 和概率密度函数
和概率密度函数![]() ,那么根据方差的定义:
,那么根据方差的定义:

具体可以参考:
概率论与数理统计学习笔记——第三十讲——方差定义和计算公式_预见未来to50的博客-CSDN博客_概率论方差的计算公式根据题目条件:
![]()

那么:

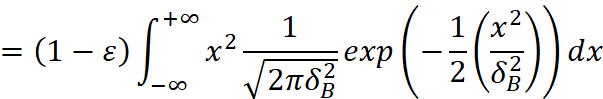

![]()
其中利用了高斯分布方差的性质:
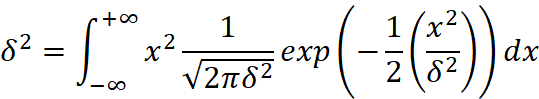
具体可以参考:
高斯分布的积分期望E(X)方差V(X)的理论推导_chaosir的博客-CSDN博客_混合高斯分布的期望与方差
证明完毕。
2. 求BLUE
由性质,![]() 独立,那么
独立,那么![]() 也相互独立
也相互独立
具体可以参考:
X1,X2,...,Xn相互独立且服从标准正态分布,为何他们的平方也相互独立? - 知乎
特殊的,如果x 服从高斯分布:
![]()
那么![]() 服从卡方分布,根据书上公式(3.19)的推导可以得到:
服从卡方分布,根据书上公式(3.19)的推导可以得到:
![]()
因此,如果我们考虑:
![]()
那么由上述分析,![]() 也是IID,因此:
也是IID,因此:
![]()
![]()
![]()
其中:
![]()
![]() 是单位矩阵。
是单位矩阵。
由![]() ,得到:
,得到:
![]()
因此:
![]()
根据BLUE,可以得到![]() 的BLUE估计为:
的BLUE估计为:

这个和MVU估计一致。
根据题目条件,已知![]() 的BLUE,且
的BLUE,且![]() 已知,他们直接存在:
已知,他们直接存在:
![]()
求![]() 的BLUE,利用习题6.12的结果,可以得到:
的BLUE,利用习题6.12的结果,可以得到:

因此:
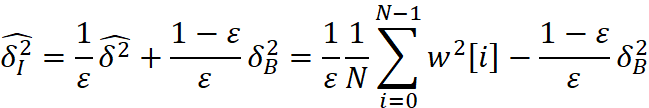
![[Java安全]—Tomcat反序列化注入回显内存马](https://img-blog.csdnimg.cn/img_convert/68fb1115241445ff6481271b7d748755.png)
![[附源码]计算机毕业设计JAVA学生信息管理系统](https://img-blog.csdnimg.cn/0dc53ca94efd4ea482ce17d1b1516459.png)






![[静态时序分析简明教程(八)]虚假路径](https://img-blog.csdnimg.cn/b7bb17870a764c6f923d00c99379c0a5.png)

![[附源码]计算机毕业设计springboot医疗器械公司公告管理系统](https://img-blog.csdnimg.cn/9c2d8d3841234e129d9f75ec69edfcf2.png)