【九章刷题录】C/C++：数组中重复的数字（JZ3）

news2024/11/25 7:19:51

  精品题解 👉 九章刷题录👈 猛戳订阅

JZ3 - 数组中重复的数字

📜 目录：

「 法一 」暴力大法（BF）

「 法二 」排序 + 遍历

「 法三 」哈希集合

「 法四 」哈希无序集

「 法五 」原地哈希

「 法六 」Map 查字典大法

「 法七 」ST 数组

🔗 题目链接：数组中重复的数字

📚 题目描述：在一个长度为 n 的数组里的所有数字都在 0 到 n-1 的范围内。 数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如，如果输入长度为 7 的数组 [2,3,1,0,2,5,3] ，那么对应的输出是 2 或者 3。存在不合法的输入的话输出 -1。 

  • 数据范围：0\leq n\leq 10000   
  • 进阶：时间复杂度 O(n)，空间复杂度 O(n)  
输入：[2,3,1,0,2,5,3]
返回值：2
说明：2或3都是对的

💭 模板：C

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 
 * @param numbers int整型一维数组 
 * @param numbersLen int numbers数组长度
 * @return int整型
 */
int duplicate(int* numbers, int numbersLen ) {
    // write code here
}

💭 模板：C++

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param numbers int整型vector 
     * @return int整型
     */
    int duplicate(vector<int>& numbers) {
        // write code here
    }
};

「 法一 」暴力大法（BF）

💡 思路：内外双 for 暴力搜索

最容易想到的方法，简单粗暴， 直接两层循环暴力遍历！外层循环依次选定一个数字作为 锚点 (Anchor) 。内层循环遍历锚点数字之后的数字 (target)，当找到相同的数字时退出循环返回该数字 (target)。全部遍历完后仍未找到，按题目要求返回 -1 即可。

两层循环时间复杂度为 O(n^2)，空间复杂度为 O(1) 。

​……​

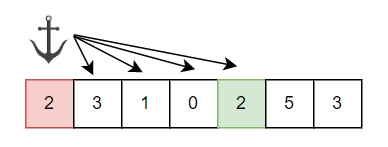
💬 代码：C

int duplicate(int* numbers, int numbersLen ) {
    // 依次设置锚点
    for (int i = 0; i < numbersLen; i++) {
        // 遍历锚点之后的数字
        for (int j = i + 1; i < numbersLen; j++) {
            if (numbers[i] == numbers[j]) {
                return numbers[i];  // 找到了
            }
        }
    }
    return -1;  // 没找到
}

💬 代码：C++

class Solution {
public:
    int duplicate(vector<int>& numbers) {
        for (int i = 0; i < numbers.size(); i++) {
            for (int j = i + 1; j < numbers.size(); j++) {
                if (numbers[i] == numbers[j]) {
                    return numbers[i];  // 找到了
                }
            }
        }
        return -1;   // 没找到
    }
};

「 法二 」排序 + 遍历

💡 思路：排序后相同的元素会紧挨着

在允许修改原数组的前提下，我们可以尝试 "排序 + 遍历" 的方法，先对数组进行排序，因为 排序后，相同的元素肯定是紧挨着的，如此一来，我们只需要一层循环遍历整个数组即可。遍历时将下标 i 设置从 1 开始，依次和 i-1 下标的元素做对比即可。

如果使用系统函数 sort，或手写堆排序等，排序所需时间复杂度为 O(nlogN)，随后只需遍历一次数组所以为 O(n)，所以总的时间复杂度为 O(nlogN)，空间复杂度为 O(1) 。相较于 "法一" 的 O(n^2) 的暴力，好多了。 

💭 代码：C

    int cmp(const void* a, const void* b) {
        return (*(int*)a - * (int*)b);
    }
int duplicate(int* numbers, int numbersLen ) {
    // 使用qsort对数组进行升序排序
    qsort(numbers, numbersLen, sizeof(int), cmp);

    // 检查相邻元素是否相等
    for (int i = 1; i < numbersLen; i++) {
        if (numbers[i] == numbers[i - 1]) {
            return numbers[i];
        }
    }
    return -1;
}

我们可以使用简单快捷的 qsort 函数，使用此函数另写一个 cmp 函数即可。排序完毕后直接遍历数组检查相邻元素是否相等即可。

💭 代码：C++

class Solution {
public:
    int duplicate(vector<int>& numbers) {
        // 直接调用 sort 排序
        sort(numbers.begin(), numbers.end());
        
        // 遍历数组，前后挨个比对
        for (int i = 1; i < numbers.size(); i++) {
            // 如果前后元素一致
            if (numbers[i] == numbers[i - 1]) {
                return numbers[i];   // 找到了
            }
        }
        return -1;    // 没找到
    }
};

C++ 做排序就更方便了，直接调 sort 就行，传入 vector 的 begin 和 end 即可。

「 法三 」哈希集合

💡 思路：集合的元素是唯一的

稍稍思考一下，既然要找重复的元素，本质上就是看是否 unique (唯一)，这让我们想到了数学中的集合，可以利用 "集合元素是唯一的" 的特点。拿题目中的例子来说，如果我们以集合的方式存储一遍该数组，那么如果在存储过程中出现重复，那么不就找到我们想要的 target 了吗？

[2,3,1,0,2,5,3]\rightarrow \left \{ 2,3,1,0,5,3 \right \}\, \, \setminus 2

回到语言角度，我们可以考虑使用 set 集合，该容器底层是红黑树，该部分时间复杂度为 O(logN) ，和 "法二" 一样只需遍历一遍数组即可，所以时间复杂度为 O(n) ，由于使用 set 要额外开空间，在悲观情况下 (没有找到返回 -1) 需要将全部元素存入，因此空间复杂度为 O(n)。

遍历数组，我们可以通过 count 接口检查集合中是否存在该数字，如果已经存在，则说明找到重复的数字了，返回该数字即可。如果该数字不在集合中 (说明是第一次出现)，我们就用 insert 将该数字加入哈希表 (杂凑表) 中。遍历结束后仍未找到按题目要求我们返回 -1 即可。

那么只有两种情况：① 在集合中  ② 不在集合中，只需在循环内做一个简单的 if-else 即可。

💭 代码：C++ 实现

class Solution {
public:
    int duplicate(vector<int>& numbers) {
        set<int> s;
        for (int i = 0; i < numbers.size(); i++) {
             // 如果表中已经存在该数字 （count返回值1为存在，0不存在）
            if (s.count(numbers[i]) == 1) {
                return numbers[i];      // 找到了
            }
            else {    // 不存在，首次出现
                s.insert(numbers[i]);   // 记录到表中
            }
        }
        return -1;    // 没找到
    }
};

我们首先定义 set，模板设为 <int>。随后遍历整个数组，我们使用 count 接口来检查是否存在该数字。count 接收一个参数，此参数表示容器中是否存在需要检查的元素。count 的返回值：如果元素存在于容器中则返回1，否则返回 0。 所以我们将当前数字传入 count，如果返回值为 1 则存在，返回即可。如果不存在我们就调用 insert，将当前数字传给 insert 将该数字添加到集合中即可。

「 法四 」哈希无序集

💡 思路：尝试把容器换成 unordered_set

此法属于 「法三」的小优化，我们知道，set 的底层是红黑树，时间复杂度为 O(logN)，但而 unordered_set 的期望复杂度能够达到 O(1)。显然使用 unordered_set 更优。

我们来简单介绍一下该容器，unordered_set 即 无序集。是一种不按特定顺序存储唯一元素的关联容器，允许根据元素的值快速检索单个元素。在 unordered_set 内部的元素不会按任何顺序排序，而是通过元素值的 hash 值将元素分组放置到各个槽中，其采用 vector + list 开链法，能通过元素值快速访问各个对应的元素，均摊耗时为 O(1)，相较于「法三」的 set 有小小的提升。但还是要遍历一次数组，所以时间复杂度还是 O(n)，并且仍然额外开空间，所以空间复杂度为 O(n)。

unordered_set 我们仍然是用 count 来检查是否在 hash 表内，用 insert 来插入。和 「法三」一样，只是容器换成了 unordered_set 而已。

⚡ 代码：C++ 实现

#include <unordered_set>
class Solution {
public:
    int duplicate(vector<int>& numbers) {
        unordered_set<int> u_set;
        for (int i = 0; i < numbers.size(); i++) {
            // 如果表中已经存在该数字 （count返回值1为存在，0不存在）
            if (u_set.count(numbers[i]) == 1) {
                return numbers[i];   // 找到了
            }
            else {   // 不存在，首次出现
                u_set.insert(numbers[i]);   // 记录到表中
            }
        }
        return -1;   // 没找到
    }
};

我们首先定义 unordered_set，模板设为 <int>。随后遍历整个数组，我们使用 count 接口来检查是否存在该数字，count 接收一个参数，此参数表示容器中是否存在需要检查的元素。如果元素存在于容器中则返回1，否则返回 0。所以我们将当前数字传入 count，如果返回值为 1 则存在，返回即可。如果不存在我们就调用 insert，将当前数字传给 insert 将该数字添加到集合中即可。

「 法五 」原地哈希

💡 思路：

再读一遍题干 —— "在一个长度为 n 的数组里的所有数字都在 0 到 n-1 的范围内" 可知：数组长度为 n，且数组中所有数字都在 [0,n-1] 内，我们可以用 swap 函数将数组中的数对应到数组下标上。首先遍历整个数组：

① 如果 numbers[i] 等于下标 i，则判断下一个下标是否对应。

② 如果 numbers[i] 不等于下标 i，那么：

  • 如果 numbers[i] == numbers[numbers[i]]，那么此时对应下标 i 的 numbers[i] 已经对应，则说明出现了重复的数字。
  • 否则 swap(numbers[numbers[i]], numbers[i]) 

③ 当遍历结束后都没有找到重复的数字，根据题目要求返回 -1。

时间复杂度为 O(n)，空间复杂度为 O(n)。

💬 代码：C++ 实现

class Solution {
public:
    int duplicate(vector<int>& numbers) {
        int i = 0;
        while (i < numbers.size()) {
            if (i == numbers[i]) {
                i++;
            }   
            else {
                if (numbers[numbers[i]] == numbers[i]) {
                    return numbers[i];
                }
                else {
                    // 交换
                    std::swap(numbers[numbers[i]], numbers[i]); 
                }
            }
        }
        return -1;
    }
};

「 法六 」Map 查字典大法

💡 思路：直接用 map 统计

在遍历的过程中使用 map 记录当前数字，存在就记为1，遍历前这个数如果已经存在则说明该数字重复。我们可以通过 count 来检查数字是否为 1，发现是 1 就说明找到了重复的了。

定义 map<int,int>，map 部分的时间复杂度为 O(nlogN)，遍历一遍数组是 O(n)。由于使用了
额外空间，空间复杂度为 O(n)。

当然，我们可以换用 unordered_map 容器，其期望复杂度为 O(1)。

💭 代码：C++ 实现

class Solution {
public:
    int duplicate(vector<int>& numbers) {
        map<int, int> m;
        for (int i = 0; i < numbers.size(); i++) {
            if (m.count(numbers[i]) > 0) {
                return numbers[i];
            }
            else {
                m[numbers[i]] = 1;
            }
        }
        return -1;
    }
};

⚡ 优化：使用 unorderd_map

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param numbers int整型vector 
     * @return int整型
     */
    int duplicate(vector<int>& numbers) {
        unordered_map<int, int> m;
        for (int i = 0; i < numbers.size(); i++) {
            if (m.count(numbers[i]) > 0) {
                return numbers[i];
            }
            else {
                m[numbers[i]] = 1;
            }
        }
        return -1;
    }
};

「 法七 」ST 数组

💡 思路：ST 数组

在遍历数组时，使用 st 数组记录当前数字，如果该数存在则说明该数字重复。由于要遍历数组，时间复杂度为 O(n)，由于使用了额外的空间开辟了新的数组，大小取决于值域，空间复杂度为 O(R(f))。

💭 代码：C++ 实现

class Solution {
public:
    int duplicate(vector<int>& numbers) {
        bool st[10000] = { 0 };   // 初始化为0
        for (int i = 0; i < numbers.size(); i++) {
            if (st[ numbers[i] ] != 0) {   // 如果不为0
                return numbers[i];
            }
            st[ numbers[i] ] = 1;    // 设置为1
        }
        return -1;
    }
};

定义布尔数组 st 用来记录每个数字是否已经出现过，并将所有元素初始化为 0。然后我们循环遍历数组 numbers 中的每个元素。对于每个元素 numbers[i]，检查 st[numbers[i]] 是否为0。如果不为0，说明该元素已经出现过，就可以返回该元素作为重复的数字。如果 st[numbers[i]] 为0，表示该元素还未出现过，将 st[numbers[i]] 设置为1，表示该元素已经出现过。如果遍历完都没有找到重复的数字，根据题意返回 -1 即可。

​

📌 [ 笔者 ]   王亦优
📃 [ 更新 ]   2023.5.24
❌ [ 勘误 ]   /* 暂无 */
📜 [ 声明 ]   由于作者水平有限，本文有错误和不准确之处在所难免，
              本人也很想知道这些错误，恳望读者批评指正！

📜 参考资料 

C++reference[EB/OL]. []. http://www.cplusplus.com/reference/.

Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. .

百度百科[EB/OL]. []. https://baike.baidu.com/.

数组中重复的数字_牛客题霸_牛客网

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/566538.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

北京筑龙作为软件服务商出席《国企阳光采购标准》研讨会

北京筑龙作为软件服务商出席《国企阳光采购标准》研讨会

近日&#xff0c;由中国企业国有产权交易机构协会市场创新专业委员会主办、青岛产权交易所有限公司承办的《国企阳光采购标准》研讨会在青岛召开&#xff0c;该会议共有19家已开展采购业务的各地产权交易机构参加&#xff0c;北京筑龙作为软件服务商出席会议。 《国企阳光采购标…
阅读更多...
【Linux】线程同步

【Linux】线程同步

文章目录 条件变量相关函数初始化条件变量-pthread_cond_init销毁条件变量-pthread_cond_destroy等待条件变量-pthread_cond_wait唤醒等待条件变量pthread_cond_broadcastpthread_cond_signal 小例子关于等待函数的补充条件变量使用规范 条件变量相关函数 初始化条件变量-pthr…
阅读更多...
多台linux设备之间设置免密登陆

多台linux设备之间设置免密登陆

1、首先&#xff0c;先搞一个公钥&#xff0c;如果已经有公钥了&#xff0c;请自行跳过 我这是有了&#xff0c;如果没有&#xff0c;也没关系&#xff0c;造一个就好&#xff0c;命令为&#xff1a; ssh-keygen -t rsa 一路回车就行&#xff0c;看下执行结果&#xff1a; 2、…
阅读更多...
使用AWTK实现汽车仪表Cluster/DashBoard嵌入式开发概述

使用AWTK实现汽车仪表Cluster/DashBoard嵌入式开发概述

AWTK=Toolkit AnyWhere，一款国产免费开源工具，ZLG开发的开源GUI引擎，为嵌入式等系统提供图形界面开发IDE。 随着汽车技术的发展，汽车仪表盘也在快速发展，从最初的机械式到电气式，再到数字化。这次电动化、智能化又一次让汽车仪表出现了飞跃式的发展，再未来，仪表板上可…
阅读更多...
【vsomeip】vsomeip安装与入门案例

【vsomeip】vsomeip安装与入门案例

&#x1f60f;★,:.☆(&#xffe3;▽&#xffe3;)/$:.★ &#x1f60f; 这篇文章主要介绍vsomeip的使用。 学其所用&#xff0c;用其所学。——梁启超 欢迎来到我的博客&#xff0c;一起学习知识&#xff0c;共同进步。 喜欢的朋友可以关注一下&#xff0c;下次更新不迷路&am…
阅读更多...
luatOS网站 lua语言学习 练习题

luatOS网站 lua语言学习 练习题

lua 教程跳转链接&#xff0c;练习题都来自这里 逻辑运算 检验大小&#xff08;自测题&#xff09; 题目&#xff1a;如果已知number变量n&#xff0c;那么如果需要判断n是否符合下面的条件&#xff1a; 3<n≤10 以下四行判断代码&#xff0c;正确的是&#xff1f; &a…
阅读更多...
【C++】运算符重载（日期类的实现）

【C++】运算符重载（日期类的实现）

【C】运算符重载&#xff08;日期类的实现&#xff09; 前言运算符重载operator全局和类中 日期类的实现成员变量的确定构造函数拷贝构造 运算符重载部分的重载思路实现GETmonthdayoperator 的重载思路实现 -的与-的重载实现 各个比较运算符的重载实现 前置与后置实现 &#xf…
阅读更多...
接口自动化【六】——接口关联之jsonpath提取+设置全局变量+通用封装

接口自动化【六】——接口关联之jsonpath提取+设置全局变量+通用封装

文章目录 前言一、jsonpath提取二、jsonpath与excel当中提取表达式结合三、类的动态属性设置四、设置全局变量&#xff08;这个模块就作为一个讲解&#xff09;五、new_handle_global_data.py六、new_handle_extract.py七、test_new_upload_image.py 文件中上传图片的代码更改八…
阅读更多...
mybatis 在当前项目中的实际应用及自定义分页的实现

mybatis 在当前项目中的实际应用及自定义分页的实现

mybatis 在当前项目中的实际应用及自定义分页的实现 项目中分页代码的解耦 实现目标 实现目标&#xff0c;使用spring 提供的分页相关的类&#xff0c;避免代码中直接使用PageHelper 具体实现 创建自定义PageHelper&#xff0c;并使用spring-data-common提供的具体实现类操…
阅读更多...
OTA升级技术概览

OTA升级技术概览

随着物联网技术的不断发展&#xff0c;越来越多的设备和系统需要进行远程升级以保持其安全性和功能性。OTA&#xff08;Over-the-Air&#xff09;升级技术是一种通过无线网络远程升级固件或软件的方法&#xff0c;已经成为现代工业、智能家居、汽车等领域中广泛应用的技术。本文…
阅读更多...
欧拉公式——最令人着迷的公式之一

欧拉公式——最令人着迷的公式之一

欧拉公式是数学里最令人着迷的公式之一&#xff0c;它将数学里最重要的几个常数联系到了一起&#xff1a;两个超越数&#xff1a;自然对数的底e&#xff0c;圆周率π&#xff1b;两个单位&#xff1a;虚数单位i和自然数的单位1&#xff0c;以及数学里常见的0。 ​而且它对数学领…
阅读更多...
generate 和 summary 配合——解析 bingchat 逻辑

generate 和 summary 配合——解析 bingchat 逻辑

generate 和 summary 配合——解析 bingchat 逻辑 new bing 微软作为 openai 公司背后的大股东&#xff0c;多年投入一朝开花结果&#xff0c;当然要把 ChatGPT 技术融入到自己的核心产品中&#xff0c;提升整体生产力。微软的第一个措施&#xff0c;就是在必应搜索引擎 bing…
阅读更多...
chatgpt赋能Python-python_span_抓取

chatgpt赋能Python-python_span_抓取

介绍 随着互联网的不断发展&#xff0c;SEO&#xff08;搜索引擎优化&#xff09;已成为所有网站主人必须面对的问题。在SEO中&#xff0c;抓取是一个非常重要的环节&#xff0c;也是一个关键性的步骤&#xff0c;它直接影响到网站的排名。 在Python编程中&#xff0c;有很多…
阅读更多...
Mac上安装多个版本的MySQL

Mac上安装多个版本的MySQL

文章目录 准备工作先确定自己机器是多少位的下载包 具体步骤1. 先安装低版本的MySQL2. 清理完后&#xff0c;再安装高版本的MySQL3. 将低版本的文件夹移回 /usr/local4. 切换版本5. 验证 扩展清理命令其他信息 准备工作 先确定自己机器是多少位的 uname -a输出X86_64&#xf…
阅读更多...
【Error】Python3.7 No module named ‘_sqlite3‘ 解决方案

【Error】Python3.7 No module named ‘_sqlite3‘ 解决方案

场景&#xff1a;docker容器运行keybert时出现错误 No module named ‘_sqlite3‘&#xff0c;是容器环境没有sqlite的库&#xff0c;如下图所示&#xff1a; 本机是能够正常导入sqlite3的&#xff0c;虚拟环境conda下也有该库。 python3.8版本的不可用于python3.7中&#xff0…
阅读更多...
【LeetCode】169. 多数元素

【LeetCode】169. 多数元素

169. 多数元素&#xff08;简单&#xff09; 方法一&#xff1a;sort排序&#xff0c;时间复杂度为O(nlogn) 思路 我自己的写法用了最简单的方法&#xff0c;首先使用 sort() 对数组元素按照从小到大进行排序&#xff0c;然后依次遍历每个元素&#xff0c;如果该元素的出现次…
阅读更多...
CompletableFuture 异步编排如何使用？

CompletableFuture 异步编排如何使用？

概述&#xff1a; 在做提交订单功能时&#xff0c;我们需要处理的事务很多&#xff0c;如&#xff1a;修改库存、计算优惠促销信息、会员积分加减、线上支付、金额计算、生成产品订单、生成财务信息、删除购物车等等。如果这些功能全部串行化处理&#xff0c;会发费很长的时间…
阅读更多...
【盘点】界面控件DevExpress WPF的几大应用程序主题

【盘点】界面控件DevExpress WPF的几大应用程序主题

DevExpress WPF控件包含了50个应用程序主题和40个调色板&#xff0c;用户可以在发布应用程序是指定主题&#xff0c;或允许最终用户动态修改WPF应用程序的外观和样式&#xff0c;其中主题带有调色板&#xff0c;可以进一步个性化您的UI&#xff01; PS&#xff1a;DevExpress …
阅读更多...
oracle WAITED TOO LONG FOR A ROW CACHE ENQUEUE LOCK问题分析

oracle WAITED TOO LONG FOR A ROW CACHE ENQUEUE LOCK问题分析

服务概述 财务系统出现业务卡顿&#xff0c;数据库实例2遇到>>> WAITED TOO LONG FOR A ROW CACHE ENQUEUE LOCK! <<<错误导致业务HANG住。 对此HANG的原因进行分析&#xff1a; 故障发生时&#xff0c;未有主机监控数据&#xff0c;从可以获取的数据库A…
阅读更多...
c++ 11标准模板（STL） std::map(三）

c++ 11标准模板（STL） std::map(三）

定义于头文件<map> template< class Key, class T, class Compare std::less<Key>, class Allocator std::allocator<std::pair<const Key, T> > > class map;(1)namespace pmr { template <class Key, class T, clas…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023