数据图形可视化

MATLAB图形窗口

函数绘制

一元函数绘制

二元函数绘图

数据图形绘制简介

离散数据可视化

连续函数可视化

二维绘图函数

基本绘图

快速方程式画图

特殊二维图形

三维绘图函数

绘制三维曲面

生成栅格数据

网格曲线绘制

隐藏线的显示和关闭

数据图形可视化

MATLAB图形窗口

MATLAB中可以使用函数Figure来建立图形窗口，在MATLAB命令框中输入Figure（x），x为正整数，就会得到图形框名称为x的图形，直接输入时默认图形框名称为1。

关闭与清除图形框

函数绘制

一元函数绘制

可以通过ezplot绘制任意一元函数：

对于显函数，fun

ezplot(fun) 绘制表达式 fun(x) 在默认定义域 -2π < x < 2π 上的图形，其中 fun(x) 仅是 x 的显函数。fun 可以是函数句柄、字符向量或字符串。

ezplot(fun,[xmin,xmax]) 绘制 fun(x) 在以下域上的图形：xmin < x < xmax。

对于隐函数，fun2(x,y)：

ezplot(fun2) 在默认域 -2π < x < 2π 和 -2π < y < 2π 中绘制 fun2(x,y) = 0。

ezplot(fun2,[xymin,xymax]) 在 xymin < x < xymax 和 xymin < y < xymax 域中制 fun2(x,y) = 0。

ezplot(fun2,[xmin,xmax,ymin,ymax]) 在 xmin < x < xmax 和 ymin < y < ymax 域中绘制 fun2(x,y) = 0。

ezplot(funx,funy) 绘制以参数定义的平面曲线 funx(t) 和 funy(t) 在默认域 0 < t < 2π 上的图形。

ezplot(funx,funy,[tmin,tmax]) 绘制 funx(t) 和 funy(t) 在 tmin < t < tmax 上的图形。

ezplot(...,fig) 将图窗绘制到由 fig 标识的图窗窗口中。使用包含一个域的上述语法中的任意输入参数组合。域选项是 [xmin xmax]、[xymin xymax]、[xmin xmax ymin ymax] 和 [tmin tmax]。

ezplot(ax,...) 将图形绘制到坐标区 ax 中，而不是当前坐标区 (gca) 中。

h = ezplot(...) 返回图形线条或等高线对象。

f='x.^3+y.^2-3';
ezplot(f)
%x.^3+y.^2-3=0的曲线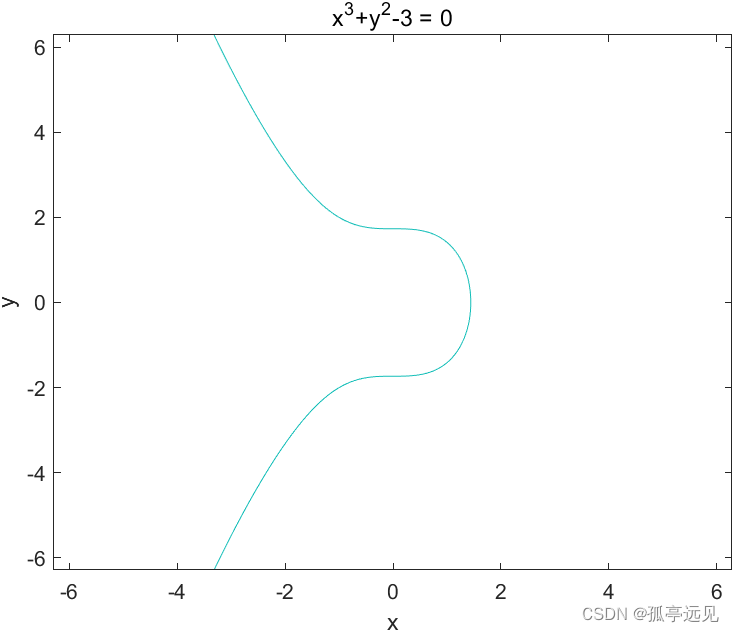

二元函数绘图

对于二元函数z=f（x，y），可以借用符号函数提供的函数ezmesh绘制各类图形，也可以用meshgrid函数获得矩阵z，或者使用循环语句for（或者while）来计算矩阵z的元素。

（1）函数ezmesh（不推荐）

ezmesh(fun) 使用 mesh 函数创建 fun(x,y) 的图形。fun 在默认域 -2π < x < 2π，-2π < y < 2π 中绘制。

ezmesh(fun,domain) 在指定的 domain 中绘制 fun。domain 可以是 4×1 向量 [xmin, xmax, ymin, ymax] 或 2×1 向量 [min, max]（其中 min < x < max，min < y < max）。

ezmesh(funx,funy,funz) 在 -2π < s < 2π 和 -2π < t < 2π 的正方形中绘制参数曲面图 funx(s,t)、funy(s,t) 和 funz(s,t)。

（2）函数fmsh

fmesh(f) 在 x 和 y 的默认区间 [-5 5] 为表达式 z = f(x,y) 创建网格图。

fmesh(f,xyinterval) 将在指定区间绘图。要对 x 和 y 使用相同的区间，请将 xyinterval 指定为 [min max] 形式的二元素向量。要使用不同的区间，请指定 [xmin xmax ymin ymax] 形式的四元素向量。

fmesh(funx,funy,funz) 在默认区间 [-5 5]（对于 u 和 v）绘制由 x = funx(u,v)、y = funy(u,v)、z = funz(u,v) 定义的参数化网格。

fmesh(funx,funy,funz,uvinterval) 在指定区间绘制参数化网格。要对 u 和 v 使用相同的区间，请将 uvinterval 指定为 [min max] 形式的二元素向量。要使用不同的区间，请指定 [umin umax vmin vmax] 形式的四元素向量。

fmesh(___,LineSpec) 设置网格的线型、标记符号和颜色。例如，'-r' 指定红色线条。在前面的任何输入参数组合之后使用此选项。

fmesh(___,Name,Value) 使用一个或多个名称-值对组参数指定网格的属性。可以将此选项与前面语法中的任何输入参数组合一起使用

（3）函数meshgrid

[X,Y] = meshgrid(x,y) 基于向量 x 和 y 中包含的坐标返回二维网格坐标。X 是一个矩阵，每一行是 x 的一个副本；Y 也是一个矩阵，每一列是 y 的一个副本。坐标 X 和 Y 表示的网格有 length(y) 个行和 length(x) 个列。

[X,Y,Z] = meshgrid(x,y,z) 返回由向量 x、y 和 z 定义的三维网格坐标。X、Y 和 Z 表示的网格的大小为 length(y)×length(x)×length(z)。

x=0:0.1:2; % 给出x 数据
y=-2:0.1:2; % 给出y 数据
[X,Y]=meshgrid(x,y); % 形成三维图形的X 和Y 数组
Z=X.^3+Y.^3;
surf(X,Y,Z);xlabel('x'),ylabel('y'),zlabel('z');
title('z=x^3+y^3')

（4）循环语句

clear all
clc
x=0:0.1:2; % 给出x 数据
y=-2:0.1:2; % 给出y 数据
z1=y.^3;
z2=x.^3;
nz1=length(z1);
nz2=length(z2);
Z=zeros(nz1,nz2);
for r=1:nz1
for c=1:nz2
Z(r,c)=z1(r)+z2(c);
end
end
surf(x,y,Z); ;xlabel('x'),ylabel('y'),zlabel('z');
title('z=x^3+y^3')

数据图形绘制简介

离散数据可视化

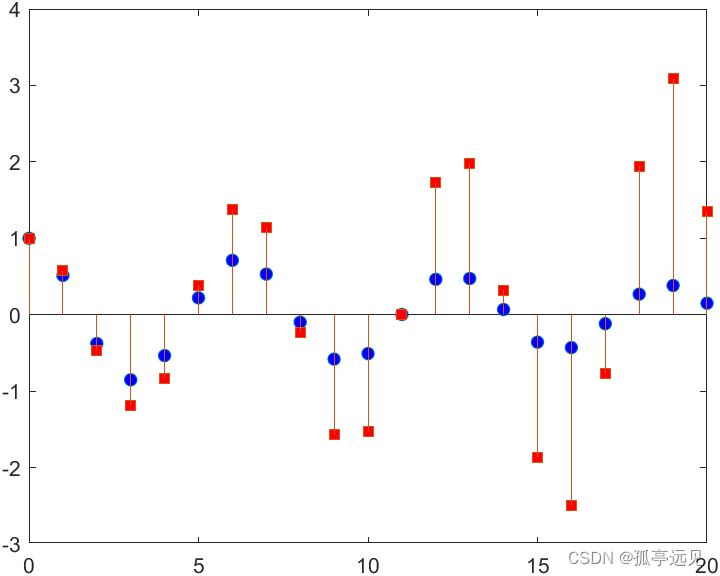
可以用stem绘制茎图：

stem(Y) 将数据序列 Y 绘制为从沿 x 轴的基线延伸的针状图。各个数据值由终止每个针状图的圆指示。

如果 Y 是向量，x 轴的刻度范围是从 1 至 length(Y)。

如果 Y 是矩阵，则 stem 将根据相同的 x 值绘制行中的所有元素，并且 x 轴的刻度范围是从 1 至 Y 中的行数。
clear all
clc
figure	
t = linspace(-2*pi,2*pi,8);
h = stem(t);
set(h(1),'MarkerFaceColor','blue')
set(h(2),'MarkerFaceColor','red','Marker','square')
stem(x,y,'option') 设置绘图时的线型、颜色等设置

stem(x,y,'filled') 填充圆。可以将此选项与前面语法中的任何输入参数组合一起使用。
clear all
clc
figure
x = 0:20;
y = [exp(-.05*x).*cos(x);exp(.06*x).*cos(x)]'; %注意此时y有两个值
h = stem(x,y);
set(h(1),'MarkerFaceColor','blue')
set(h(2),'MarkerFaceColor','red','Marker','square')

用图形表示离散函数

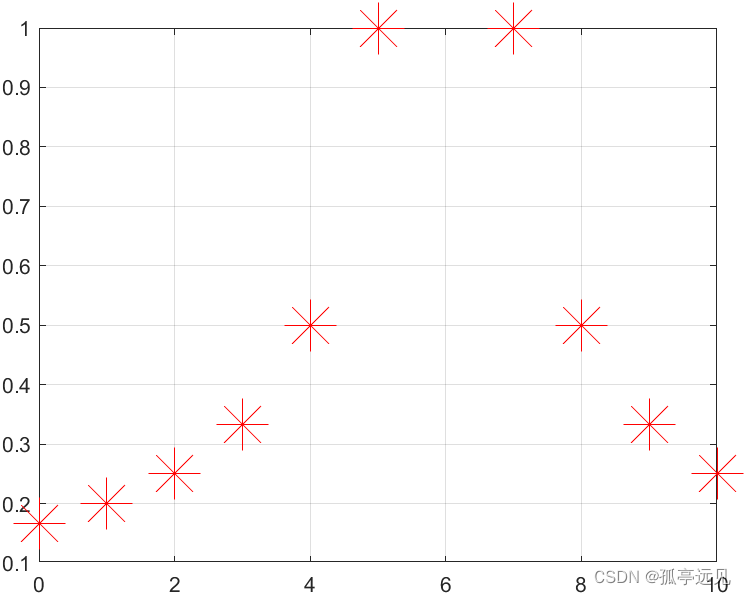
clear all
clc
n=0:10;                    % 产生一组10个自变量函数Xn
y=1./abs(n-6);               % 计算相应点的函数值Yn
plot(n,y,'r*','MarkerSize',25)
                           % 用尺寸15的红星号标出函数点
grid on                     % 画出坐标方格

连续函数可视化

对于连续函数可以取一组离散值自变量，然后计算函数值。

subplot(m,n,p) 将当前图窗划分为 m×n 网格，并在 p 指定的位置创建坐标区。按行号对子图位置进行编号。第一个子图是第一行的第一列，第二个子图是第一行的第二列，依此类推。如果指定的位置已存在坐标区，则此命令会将该坐标区设为当前坐标区。

axis(limits) 指定当前坐标区的范围。以包含 4 个、6 个或 8 个元素的向量形式指定范围。

plot(X1,Y1,LineSpec1,...,Xn,Yn,LineSpecn) 设置每个线条的线型、标记符号和颜色。您可以混用 X、Y、LineSpec 三元组和 X、Y 对组：例如plot(X1,Y1,X2,Y2,LineSpec2,X3,Y3)。

clear all
clc
t1=(0:12)/12*pi;       % 自变量取13个点
y1=sin(t1).*sin(9*t1); % 计算函数值
t2=(0:50)/50*pi;       % 自变量取51个点
y2=sin(t2).*sin(9*t2);
subplot(2,2,1);        % 在子图1上画图
plot(t1,y1,'r.');      % 用红色的点显示
axis([0,pi,-1,1]);     % 定义坐标大小
title('子图1');        % 显示子图标题
% 子图2用红色的点显示
subplot(2,2,2);
plot(t2,y2,'r.');
axis([0,pi,-1,1]);
title('子图2')
% 子图3用直线连接数据点和红色的点显示
subplot(2,2,3);
plot(t1,y1,t1,y1,'r.')
axis([0,pi,-1,1]);
title('子图3')
% 子图4用直线连接数据点
subplot(2,2,4);
plot(t2,y2);
axis([0,pi,-1,1]);
title('子图4')

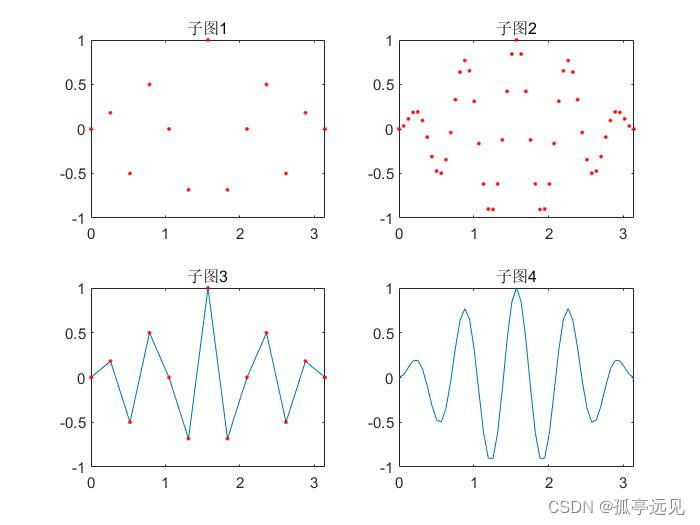
二维绘图函数

基本绘图

text(x,y,txt) 使用由 txt 指定的文本，向当前坐标区中的一个或多个数据点添加文本说明。若要将文本添加到一个点，请将 x 和 y 指定为标量。若要将文本添加到多个点，请将 x 和 y 指定为长度相同的向量。

clear all
clc
x = 0 :0.1 : 4*pi;
y = exp ( 2*cos ( x ) );

figure(1)

plot(x,y,'b.')
title('test')            % 图名
xlabel('x'); 
ylabel('y')            % 轴名
legend('e2cosx')         % 图例
text(2,0.5,'y= e2cosx ')    % 文字
axis([0,4*pi,-1,1])        %设置轴的范围
grid on           %画坐标分隔线

clear all
clc
t=(0:pi/5:2*pi)';       % 横坐标列向量
k=0.3:0.1:1;          %8个幅值
Y=cos(t)*k;          % 8条函数值矩阵
plot(t,Y)

clear all
clc
t=(0:pi/100:4*pi)';                  % 长度为101的时间采样序列，'表示转置
y1=sin(t)*[1,-1];                   % 包络线函数值，101×2矩阵
y2=sin(t).*sin(9*t);                 % 长度为101的调制波列向量
t3=pi*(0:9)/9;
y3=sin(t3).*sin(9*t3);
plot(t,y1,'r:',t,y2,'b',t3,y3,'b*')          % 绘制三组曲线
axis([0,2*pi,-1,1])                   % 控制轴的范围

clear all
clc
t=linspace(0,2*pi,100)';                              % 产生100个数
X=[cos(t),cos(2*t),cos(3*t)]+i*sin(t)*[1,1,1];             %100x3的复数矩阵
plot(X),axis square;                                 %使坐标轴长度相同
legend('1','2','3')

clear all
clc
th=[0:pi/50:2*pi]';
a =[0.5:.5:4.5];
X =cos(th)*a;
Y =sin(th)*sqrt(25-a.^2);
plot(X,Y)
axis('equal')
xlabel('x')
ylabel('y')
title('A set of Ellipses')

Z=peaks 返回在一个 49×49 网格上计算的 peaks 函数的 z 坐标。

示例

Z=peaks(n) 返回在一个 n×n 网格上计算的 peaks 函数。如果将 n 指定为长度为 k 的向量。
z = peaks
plot(z)
y=1:length(peaks)
plot(peaks,y)

快速方程式画图

fplot

clear all
clc
fplot('x-cos(x^2)-sin(2*x^3)',[-4,4])   %绘制图形

ezplot

clear all
clc
ezplot('x^2')  %绘制图形

特殊二维图形

（1）极坐标

polarplot(theta,rho) 在极坐标中绘制线条，由 theta 表示弧度角，rho 表示每个点的半径值。输入必须是长度相等的向量或大小相等的矩阵。如果输入为矩阵，polarplot 将绘制 rho 的列对 theta 的列的图。也可以一个输入为向量，另一个为矩阵，但向量的长度必须与矩阵的一个维度相等。

polarplot(theta,rho,LineSpec) 设置线条的线型、标记符号和颜色。

clear all
clc
t=0:0.1:3*pi;    %极坐标的角度.
polarplot(t,abs(cos(5*t)));

（2）对数坐标系

对数坐标曲线函数：semilogx, semilogx(y), semilogy

semilogx(X,Y) 在 x 轴上使用以 10 为底的对数刻度、在 y 轴上使用线性刻度来绘制 x 和 y 坐标。

semilogx(Y) 绘制 Y 对一组隐式 x 坐标的图,X的坐标刻度为对数，Y为线性刻度。

如果 Y 是向量，则 x 坐标范围从 1 到 length(Y)。

如果 Y 是矩阵，则对于 Y 中的每个列，图中包含一个对应的行。x 坐标的范围是从 1 到 Y 的行数。

如果 Y 包含复数，semilogx 绘制 Y 的虚部对 Y 的实部的图。

semilogy(X,Y) 在 x 轴上使用线性刻度、在 y 轴上使用以 10 为底的对数刻度来绘制 x 和 y 坐标。

clear all
clc
t = 0 : 900; 
A = 1000;  
a = 0.005; 
b = 0.005;	
z1 = A * exp ( -a * t );  		 %对数函数
z2 = sin ( b * t );      	      %正弦函数
[ haxes, hline1, hline2 ] = plotyy ( t, z1, t, z2, 'semilogy', 'plot' );
axes ( haxes ( 1 ) )
ylabel ( '对数坐标' )
axes ( haxes ( 2 ) )
ylabel ( '直角坐标' )
set (hline2, 'LineStyle', ' -- ' )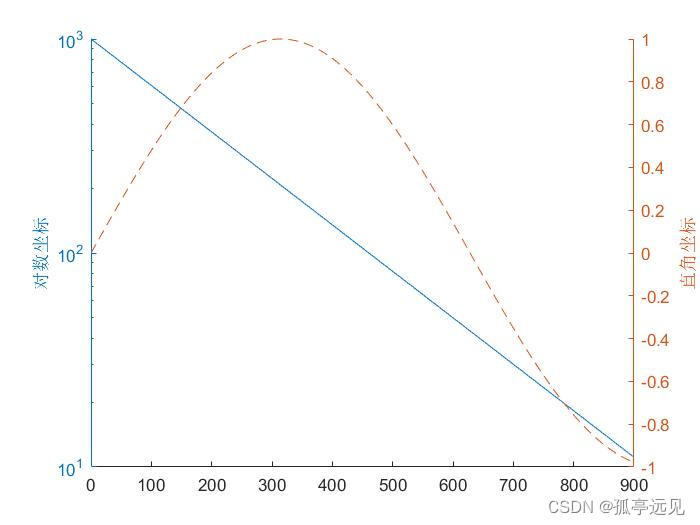

（3）柱坐标系：pol2cart

（4）球坐标系：sph2cart

(5)饼图

clear all
clc
x=[13,28,23,43,22];
pie(x)

将某一部分切开：

clear all
clc
x=[13,28,23,43,22];
y=[0 0 0 0 1]
pie(x,y)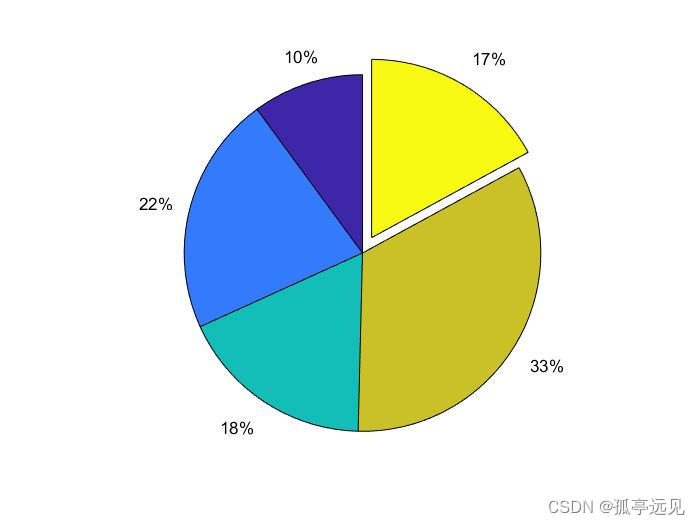

不断增加axis square后，绘制出的图形会越来越扁平

如果加入命令axis equal tight，则会绘出最扁平的椭圆图形

三维绘图函数

绘制三维曲面

可以使用mesh、meshc或者meshz来绘制不同形式的网格曲面。

使用函数surf、surfc来绘制三维网格曲面

surf(X,Y,Z) 创建一个三维曲面图，它是一个具有实色边和实色面的三维曲面。该函数将矩阵 Z 中的值绘制为由 X 和 Y 定义的 x-y 平面中的网格上方的高度。曲面的颜色根据 Z 指定的高度而变化。

surfc(X,Y,Z) 创建一个三维曲面图，其下方有等高线图。曲面图是一个具有实色边和实色面的三维曲面。该函数将矩阵 Z 中的值绘制为由 X 和 Y 定义的 x-y 平面中的网格上方的高度。曲面的颜色根据 Z 指定的高度而变化。

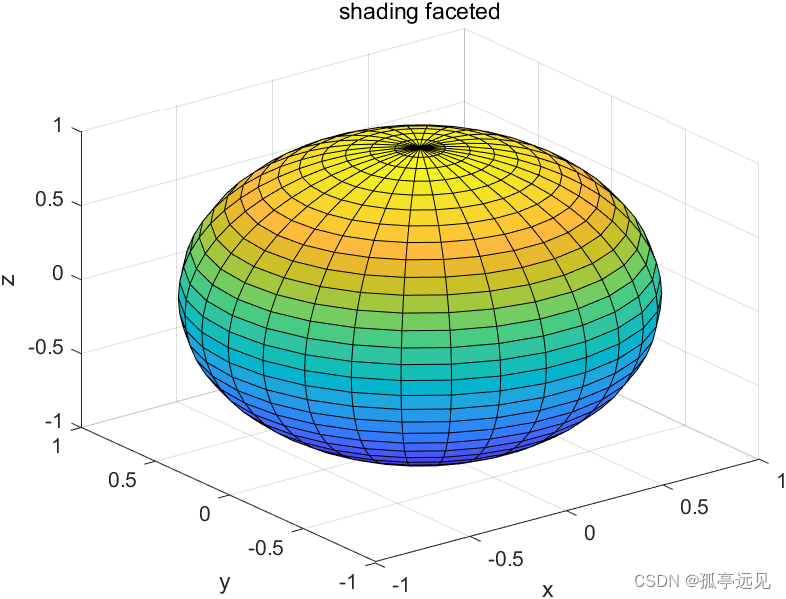
[X,Y,Z] = sphere 返回球面的 x、y 和 z 坐标而不对其绘图。返回的球面的半径等于 1，由 20×20 个面组成。该函数以三个 21×21 矩阵形式返回 x、y 和 z 坐标。要使用返回的坐标绘制球面，请使用 surf 或 mesh 函数。

[X,Y,Z] = sphere(n) 返回半径等于 1 且包含 n×n 个面的球面的 x、y 和 z 坐标。该函数以三个 (n+1)×(n+1) 矩阵形式返回 x、y 和 z 坐标。
clear all
clc
figure
[X,Y,Z]=sphere(30); 			%计算球体的三维坐标
surf (X,Y,Z); 				%绘制球体的三维图形
xlabel('x'),
ylabel('y'),
zlabel('z');
title(' shading faceted ');
注意：在图形窗口，需要将图形属性Renderer设置为Painters，才能显示出坐标名词和图形标题。

生成栅格数据

meshgrid

[X,Y] = meshgrid(x,y) 基于向量 x 和 y 中包含的坐标返回二维网格坐标。X 是一个矩阵，每一行是 x 的一个副本；Y 也是一个矩阵，每一列是 y 的一个副本。坐标 X 和 Y 表示的网格有 length(y) 个行和 length(x) 个列。

[X,Y] = meshgrid(x) 与 [X,Y] = meshgrid(x,x) 相同，并返回网格大小为 length(x)×length(x) 的方形网格坐标。

[X,Y,Z] = meshgrid(x,y,z) 返回由向量 x、y 和 z 定义的三维网格坐标。X、Y 和 Z 表示的网格的大小为 length(y)×length(x)×length(z)。

x = 1:3;
y = 1:5;
[X,Y] = meshgrid(x,y)

%结果
X = 5×3

     1     2     3
     1     2     3
     1     2     3
     1     2     3
     1     2     3

Y = 5×3

     1     1     1
     2     2     2
     3     3     3
     4     4     4
     5     5     5

网格曲线绘制

mesh(X,Y,Z) 创建一个网格图，该网格图为三维曲面，有实色边颜色，无面颜色。该函数将矩阵 Z 中的值绘制为由 X 和 Y 定义的 x-y 平面中的网格上方的高度。边颜色因 Z 指定的高度而异。

meshc：在绘图的同时，在x-y平面上绘制函数的等值线

meshz：在网格基础上在图形的底部外侧绘制三维网格图

clear all 
clc
x=-8:0.5:8;
y=x;
[X,Y]=meshgrid(x,y);
% R=sqrt(X.^2+Y.^2)+eps;
R=sqrt(X.^2+Y.^2)
Z=sin(R)./R;
mesh(X,Y,Z)
grid on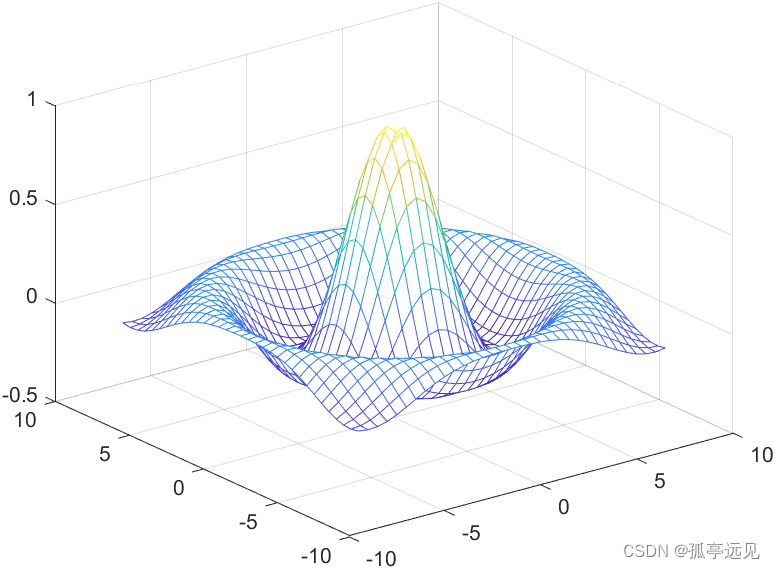

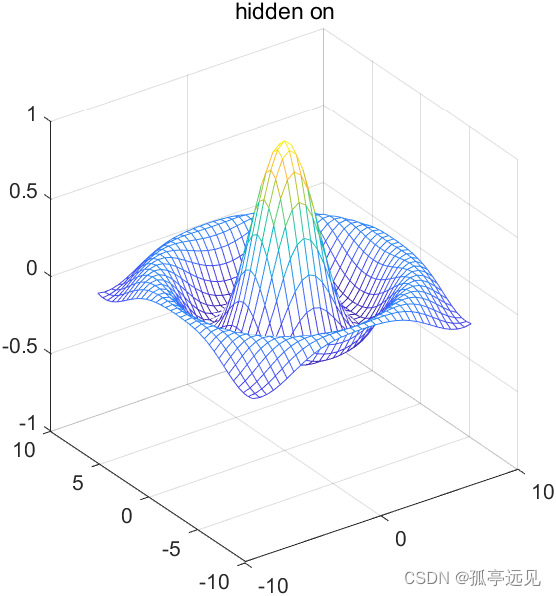
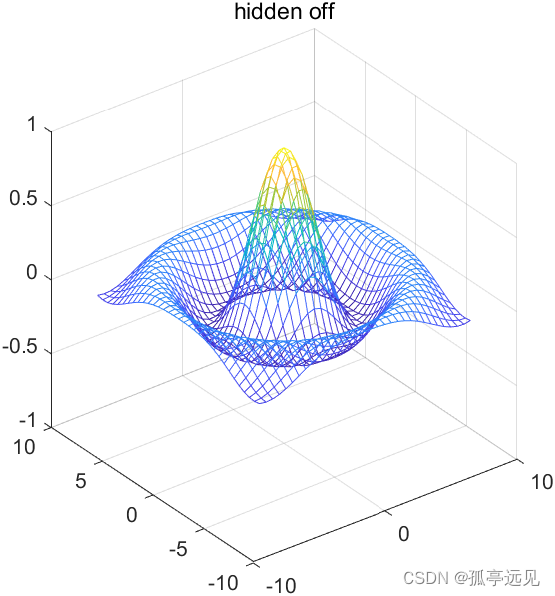
隐藏线的显示和关闭

hidden on是去掉网格曲面的隐藏线

hidden off是显示网格曲面的隐藏线

close all
clear
x=-8:0.5:8;
y=x;
[X,Y]=meshgrid(x,y);
R=sqrt(X.^2+Y.^2)+eps;
Z=sin(R)./R;
subplot(1,2,1)
mesh(X,Y,Z)
hidden on
grid on
title('hidden on')
axis([-10 10 -10 10 -1 1])
subplot(1,2,2)
mesh(X,Y,Z)
hidden off
grid on
title('hidden off')
axis([-10 10 -10 10 -1 1])