🎇C++笔试强训
- 博客主页:一起去看日落吗
- 分享博主的C++刷题日常,大家一起学习
博主的能力有限,出现错误希望大家不吝赐教- 分享给大家一句我很喜欢的话:夜色难免微凉,前方必有曙光 🌞。
💦🔥
选择题
💦 第一题
在有序双向链表中定位删除一个元素的平均时间复杂度为
A O(1)
B O(N)
C O(logN)
D O(N*logN)
查找是需要遍历,和链表数据的个数有关,所以是O(n)
这道题的答案是B
💦 第二题
在一个以 h 为头指针的单循环链表中,p 指针指向链尾结点的条件是( )
A p->nextNULL
B p->nexth
C p->next->nexth
D p->data-1
这是带头结点的单循环链表
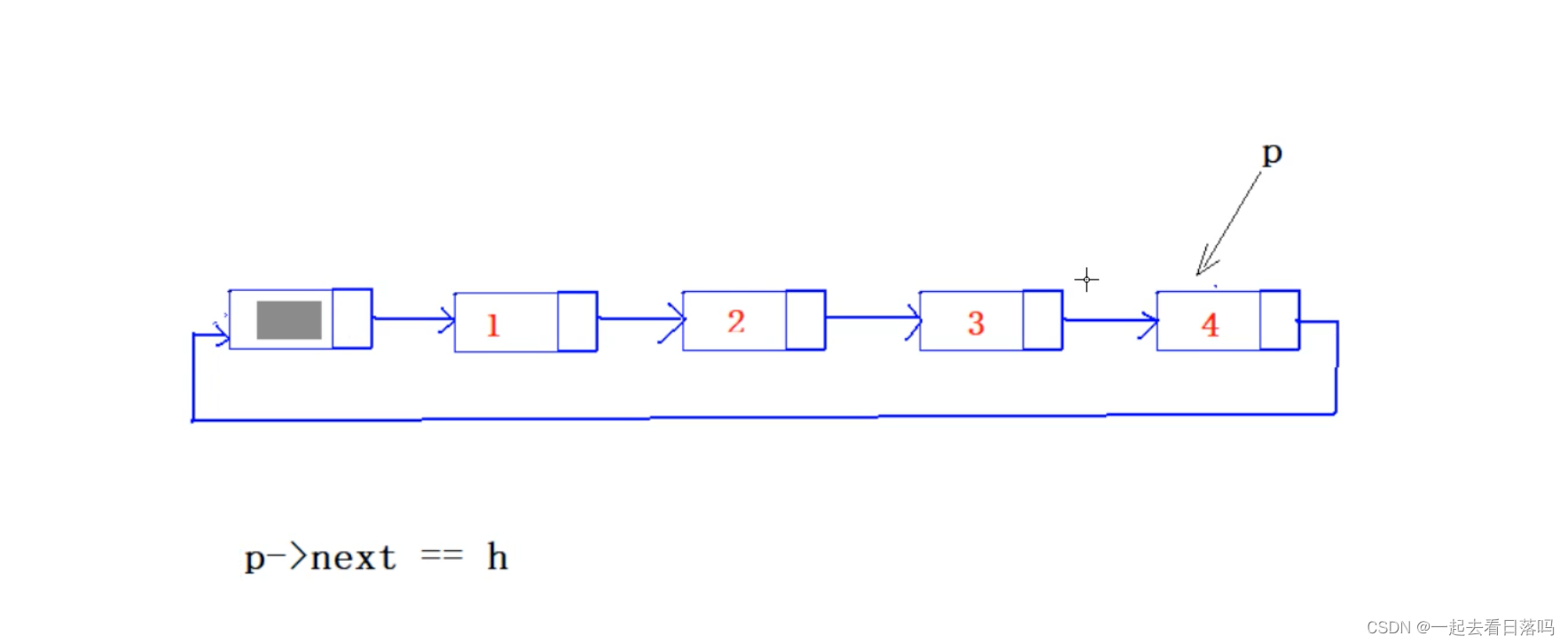
这道题的答案是B
💦 第三题
在双向链表中指针p的结点前插入一个指针q的结点操作是()
A p->Llink=q;q->Rlink=p;p->Llink->Rlink=q;q->Llink=q;
B p->Llink=q;p->Llink->Rlink=q;q->Rlink=p;q->Llink=p->Llink;
C q->Rlink=p;q->Llink=p->Llink;p->Llink->Rlink=q;p->Llink=q;
D q->Llink=p->Llink;q->Rlink=q;p->Llink=q;p->Llink=q;
数据结构的题目记得多画图!!!!
根据选项来看答案,Llink代表前驱,Rlink是后驱
A p->Llink->Rlink=q;修改没变
B p->Llink->Rlink=q 修改没变
D q->Rlink=q 修改没变

这道题的答案是C
💦 第四题
若用数组S[0…n]作为两个栈S1和S2的存储结构,对任何一个栈只有当S全满时才不能做入栈操作。为这两个栈分配空间的最佳方案是
A S1的栈底位置为0,S2的栈底位置为n
B S1的栈底位置为0,S2的栈底位置为n/2
C S1的栈底位置为1,S2的栈底位置为n/2
这道题只要读懂题就很简单
要求栈全满才能不能入栈,s1 栈底是0,s2 栈底是n
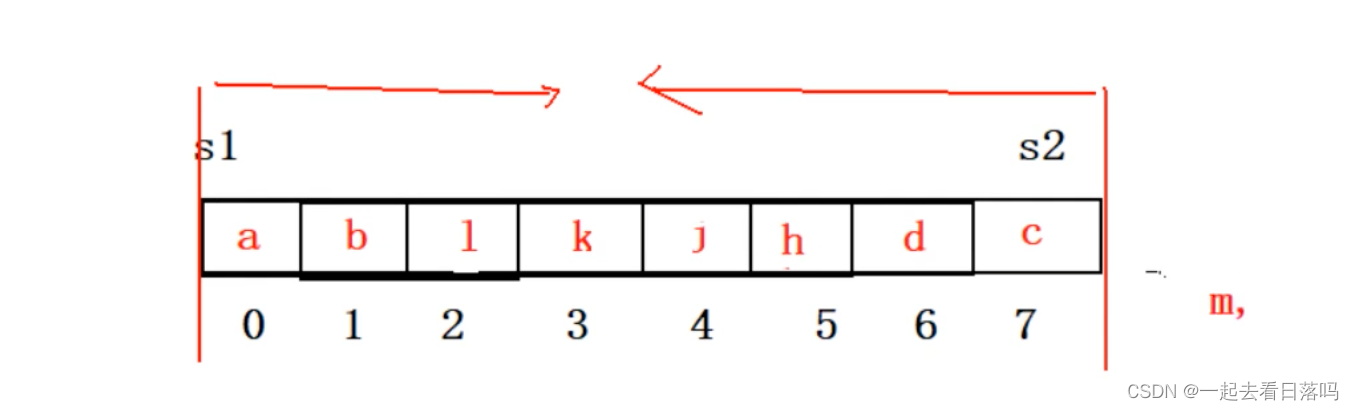
这道题的答案是A
💦 第五题
循环队列的存储空间为 Q(1:200) ,初始状态为 front=rear=200 。经过一系列正常的入队与退队操作后,front=rear=1 ,则循环队列中的元素个数为( )
A 0或200
B 1
C 2
D 199
画两百个空间和八个是一样的,所以直接画八个也可以类比画图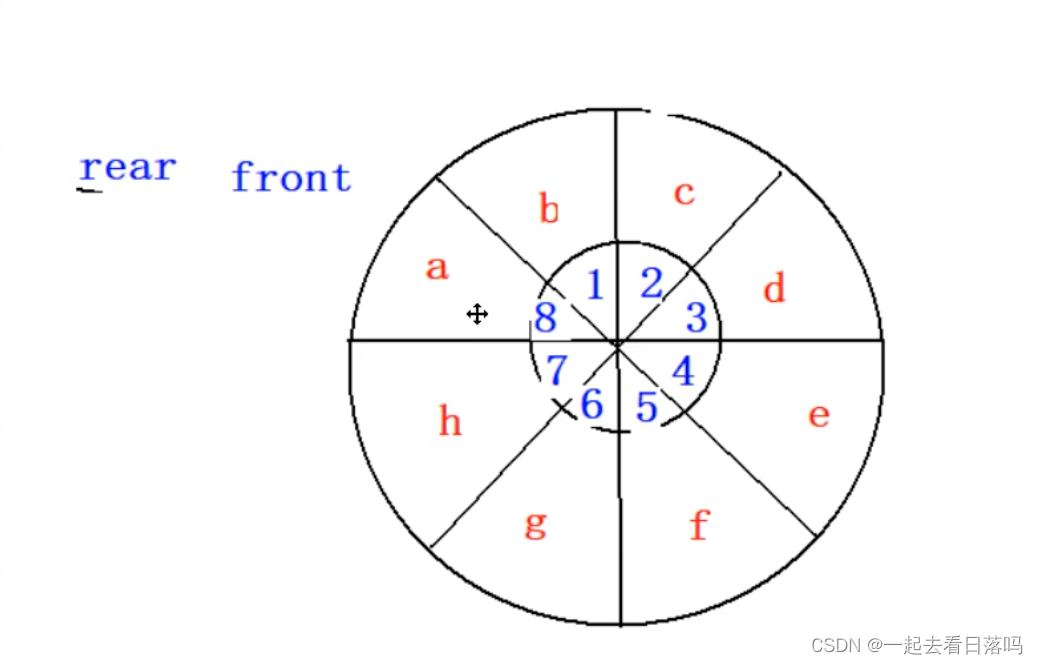
所以队满和队空都有可能,如果要判断这种情况,我们一般平时设计循环队列的时候都会设计少用一个空间,但是这个题不是这样的所以两种情况都有可能
这道题的答案是A
💦 第六题
将一棵二叉树的根结点放入队列,然后递归的执行如下操作,将出队结点所有子结点加入队。以上操作可以实现哪种遍历()
A 前序遍历
B 中序遍历
C 后序遍历
D 层序遍历
记住如果是通过栈,就有可能是前中后序,如果是队列,那就一定是层序遍历
这道题的答案是D
💦 第七题
已知数据元素为(34,76,45,18,26,54,92,65),按照依次插入节点的方法生成一棵二叉排序树,则该树的深度为()
A 7
B 6
C 4
D 5
只要画图就可以知道答案了。所以数据结构画图是必要的技能
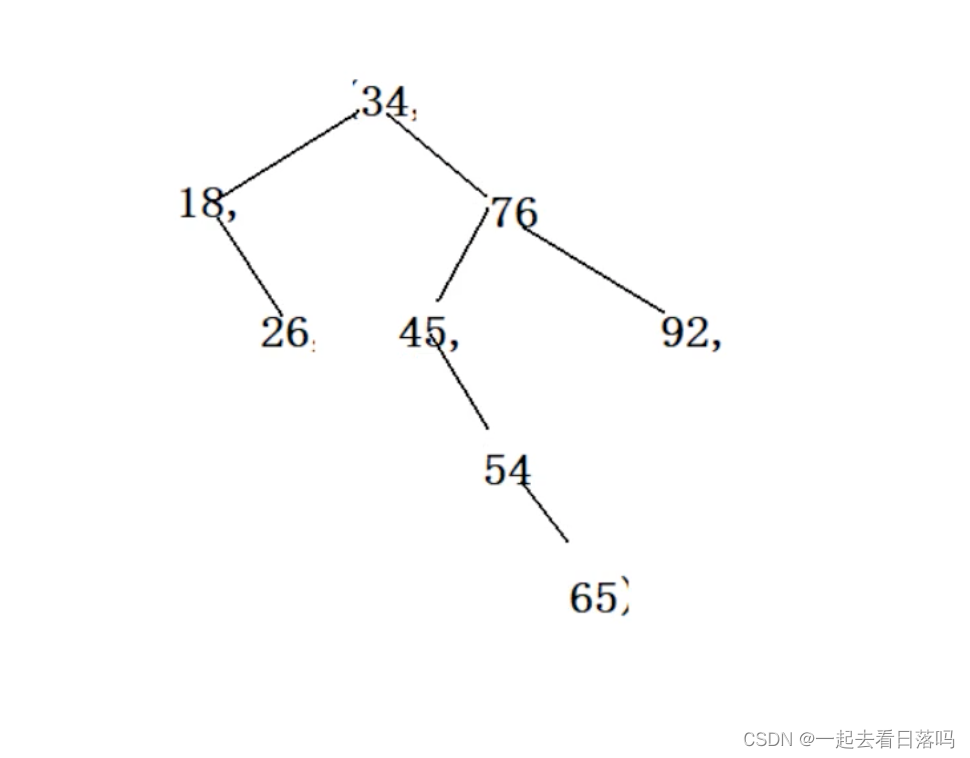
这道题的答案是D
💦 第八题
有 1000 个无序的整数,希望使用最快的方式找出前 50 个最大的,最佳的选择是( )
A 冒泡排序
B 基数排序
C 堆排序
D 快速排序
只要能排序,都能找出来,但是需要找的是最优解
冒泡排序 基数排序 快速排序 都是严格排序,都需要把所有数据排序好,堆排序只关心堆顶元素,不见得其他数据是排序好的,堆排序是个弱排序,只关心最大值。
这道题的答案是C
💦 第九题
已知一个线性表(38,25,74,63,52,48),假定采用散列函数h(key) = key%7 计算散列地址,并散列存储在散列表A[0…6]中,若采用线性探测方法解决冲突,则在该散列表上进行等概率成功查找的平均查找长度为()
A 1.5
B 1.7
C 2.0
D 2.3
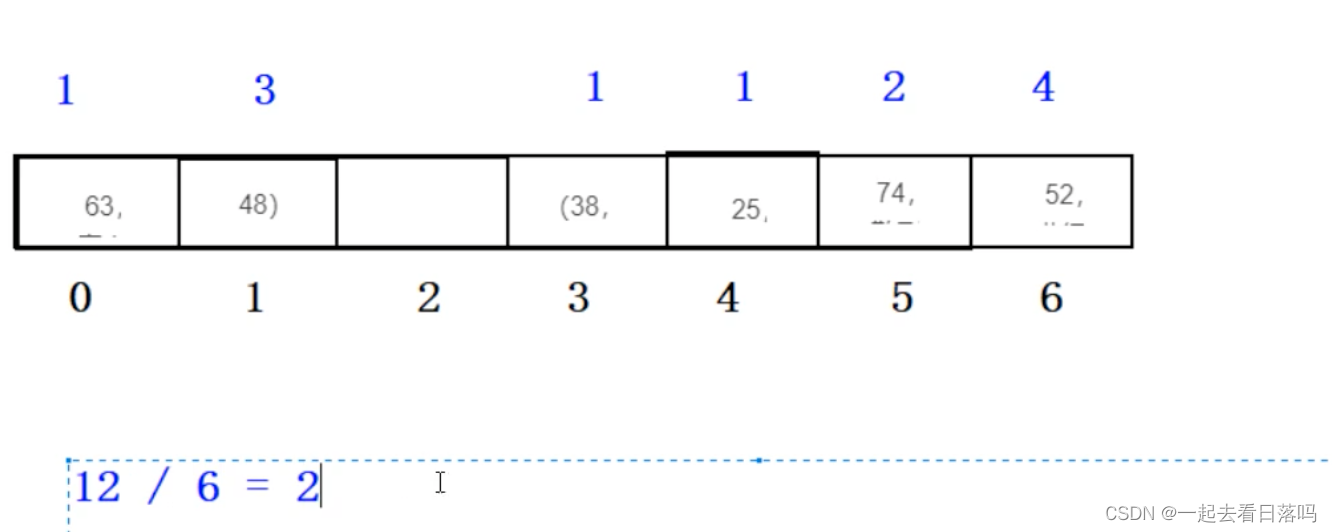
这道题的答案是C
💦 第十题
下面的排序方法中,关键字比较次数与记录的初始排列无关的是______。
A 希尔排序
B 冒泡排序
C 直接插入排序
D 直接选择排序
希尔排序是插入排序的一种,跟插入的数据是有关系的,需要进行比较
冒泡排序需要拿前面的数据和后面的进行比较,和选择的数据也有关
直接插入排序和希尔排序一样
直接选择排序正着排和倒着排都需要找最小值,每次都是遍历整个序列,所以和初始排列无关
这道题的答案是D
编程题
🔥 第一题
链接:小易的升级之路
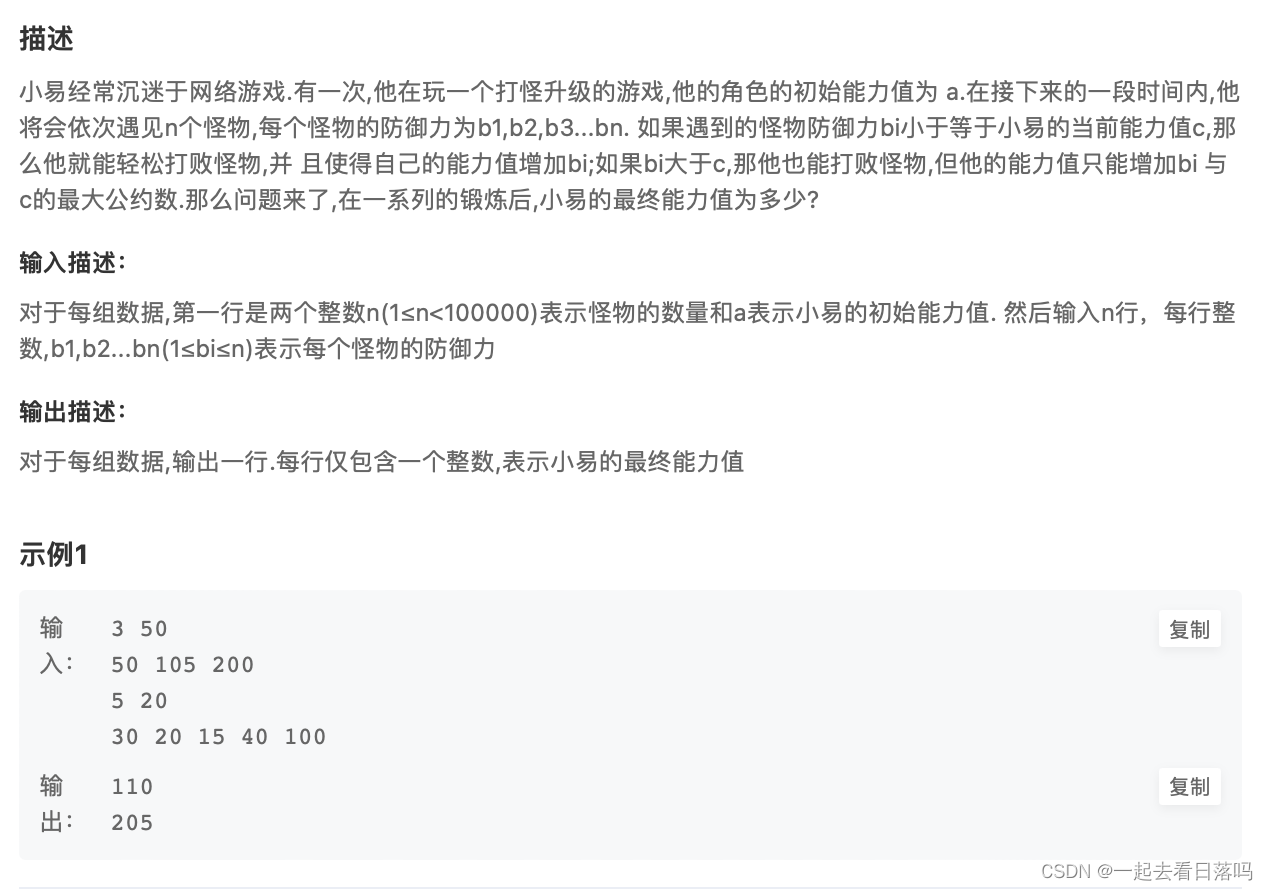
- 解题思路
本题的能力值的累加分两种情况,一种是直接相加bi,一种是累加当前能力值于bi的最大公约数。最大公约数可以通过碾转相除法求得:a与b的最大公约数相当于b与a,b余数的最大公约数。如果求余结果为0, 则b为所求结果
- 代码演示
#include <iostream>
#include <vector>
using namespace std;
int GCD(int a,int b)
{
//辗转相除法
int c;
while(c=a%b)
{
a = b;
b = c;
}
return b;
}
int getPower(int n,int a)
{
vector<int> num(n);
for(int i = 0;i < n;i++) //输入敌人的防御值
{
cin >> num[i];
}
for(int i = 0;i < n;i++)
{
if(a >= num[i])
a += num[i];
else
a += GCD(a,num[i]);
}
return a;
}
int main()
{
int n,a;
int power;
while(cin >> n >> a)
{
power = getPower(n,a);
cout << power << endl;
}
return 0;
}
🔥 第二题
链接:找出字符串中第一个只出现一次的字符
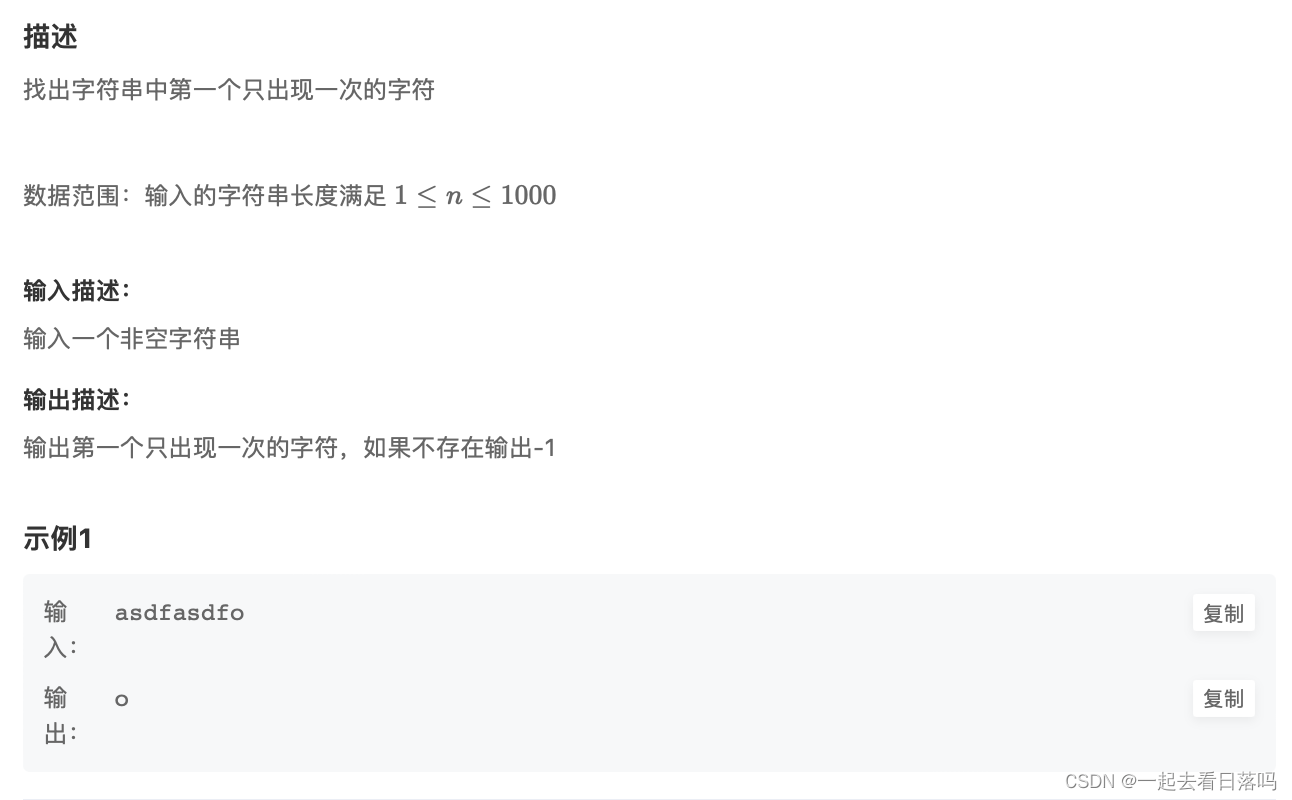
- 解题思路
用一个数组的每一个位置表示对应的位置。对应的字符位置存放字符出现的次数。统计完之后,遍历输入字符,遇到第一个只出现一次的字符就停止
- 代码演示
#include <iostream>
#include <string>
using namespace std;
//方法一:暴力法
char getFirstOneChar_1(const string &str)
{
int j;
for(int i = 0;i < str.size();++i)
{
for(j = 0;j < str.size();++j)
{
if(j == i)
{
continue;
}
if(str[j] == str[i])
{
break;
}
}
if(j >= str.size())
return str[i];
}
return -1;
}
//方法二:哈希法
char getFirstOneChar_2(const string &str)
{
int hash[256] = {0};
for(int i = 0;i < str.size();++i)//统计字符的次数
hash[str[i]]++;
for(int i = 0;i < str.size();++i)
{
if(hash[str[i]] == 1)
return str[i];
}
return -1;
}
//方法三:string 类函数查找法
char getFirstOneChar_3(const string &str)
{
for(int i = 0;i < str.size();++i)
{
int index1 = str.find(str[i]);
int index2 = str.rfind(str[i]);
if(index1 == index2)
return str[i];
}
return -1;
}
int main()
{
string str;
char res;
while(getline(cin,str))
{
//res = getFirstOneChar_1(str);
//res = getFirstOneChar_2(str);
res = getFirstOneChar_3(str);
if(res == -1)
cout << -1 << endl;
else
cout << res << endl;
}
return 0;
}