一、题目（经典动态规划）

两种形状的瓷砖（一种是12的，另一种是12+11的形状），拼2N面积，有多少种拼法（旋转图形算两种不同的，不算成同一种。）

二、解题思路

1. 铺满2*N面积：

翻译过来也即：

1. 第N-1列及之前列全满；
2. 第N列全满；
3. 第N+1列及之后列全空。

2. 对于第i列，有4种情况：

1. 一个正方形都没有被覆盖，记为状态 0；
2. 只有上方的正方形被覆盖，记为状态 1；
3. 只有下方的正方形被覆盖，记为状态 2；
4. 上下两个正方形都被覆盖，记为状态 3。

例如本题最后第N列是满的，所以i=N的时候对应状态3。

3. N-1 -> N 转移方程：

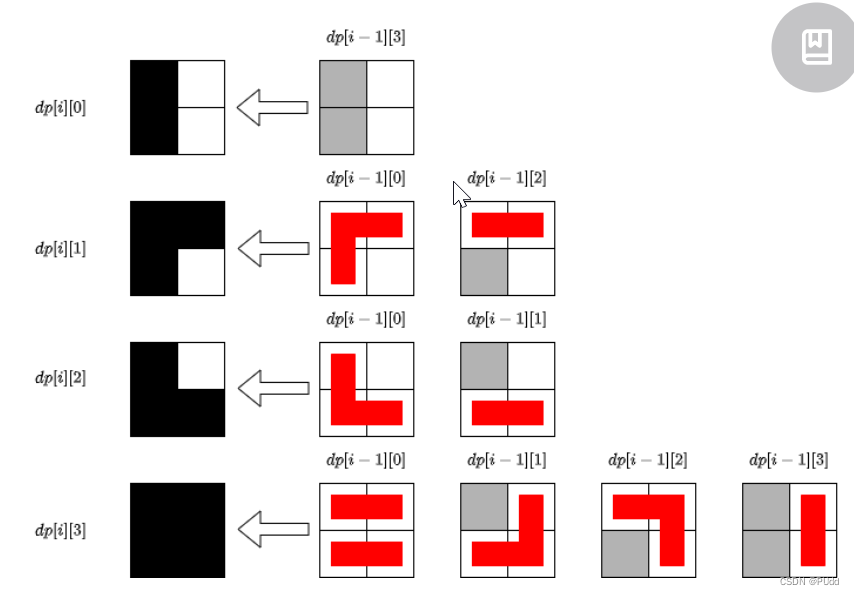
三、核心代码

dp[0][3]=1;
for(int i = 1;i <= n; i++)
{
	dp[i][0] = dp[i-1][3];
	dp[i][1] = (dp[i-1][0]+dp[i-1][2]);
	dp[i][2] = (dp[i-1][0]+dp[i-1][1]);
	dp[i][3] = (dp[i-1][0]+dp[i-1][1]+dp[i-1][2]+dp[i-1][3]);
}
return dp[n][3];

四、代码中存在的一些知识性问题

1. 二层vector的定义、初始化

二层vector的定义：

1. vector<vector<int>>(4);
2. vector<vector<int>>vec; 最后每个元素值都是int类型（本题由于最后的值会很大，故使用long long： vector<vector<long long>>）
3. vector<vector<int>>vec(5);此处表明：外层是5个元素，也即： [[],[],[],[],[]],最后每个元素值都是int类型
4. vector<vector<int>>vec(5,vector<int>(4));此处表明：外层是5个元素，内层是4个元素，且是vector<int>类型。此处为了同时定义内外层元素个数，采用了这种形式： vector<vector<long long>>dp(n+1,vector<long long>(4));（虽然不是很理解，但是也会用了）

vector大部分情况下会把值初始化为0：

1. vector默认初始化，即不指定元素个数和值，此时vector的元素个数为0
2. vector初始化指定元素个数，但不指定元素的值，此时元素的值默认初始化为0
3. vector初始化指定元素的个数和值
4. 通过rezise()函数重新调整二维vector的外层元素个数，则实际上内层vector的元素个数仍为0
5. 通过rezise()函数重新调整二维vector的内外层元素个数，若为指定初始值，则默认初始化为0
   所以在本题中， vector<vector<long long>>dp(n+1,vector<long long>(4));这一句实际上已经把所有元素初始化成0了

2. mod

题目说返回对 10^9 + 7 取模 的值，但是标答在转移方程中就取模了。所有的转移都是采用的加法，所以在中间步骤取模也没事。

五、代码的最终呈现

class Solution {
public:
    int numTilings(int n) 
    {
        long long mod = 1e9 + 7;
        vector<vector<long long>>dp(n+1,vector<long long>(4));
        dp[0][3]=1;
        for(int i = 1;i <= n; i++)
        {
            dp[i][0] = dp[i-1][3];
            dp[i][1] = (dp[i-1][0]+dp[i-1][2])%mod;
            dp[i][2] = (dp[i-1][0]+dp[i-1][1])%mod;
            dp[i][3] = (dp[i-1][0]+dp[i-1][1]+dp[i-1][2]+dp[i-1][3]) % mod;
        }
        
        return dp[n][3];
    }

这一题掺杂了个人的很多不恰当的理解orz