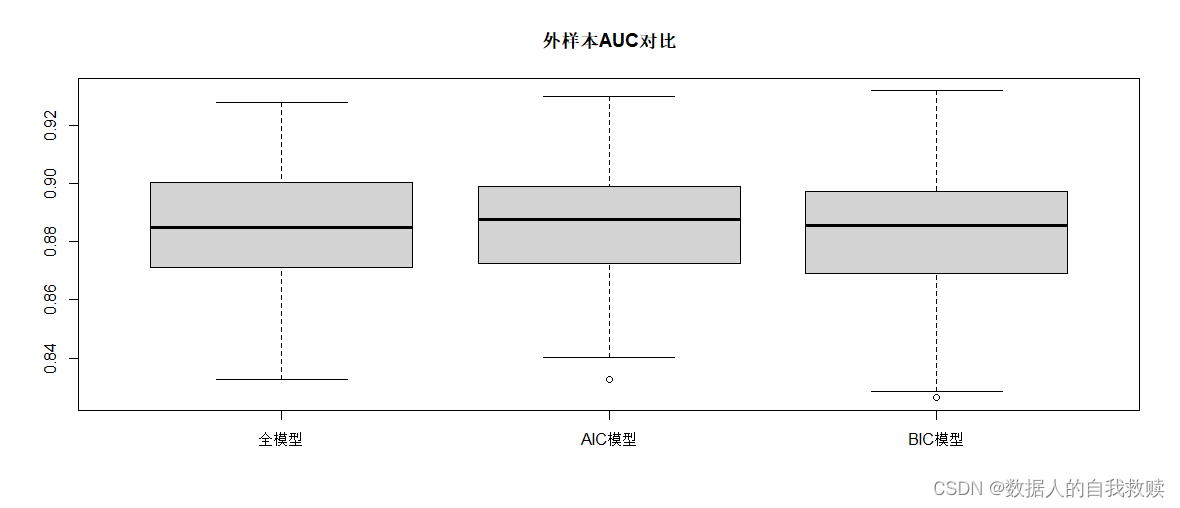
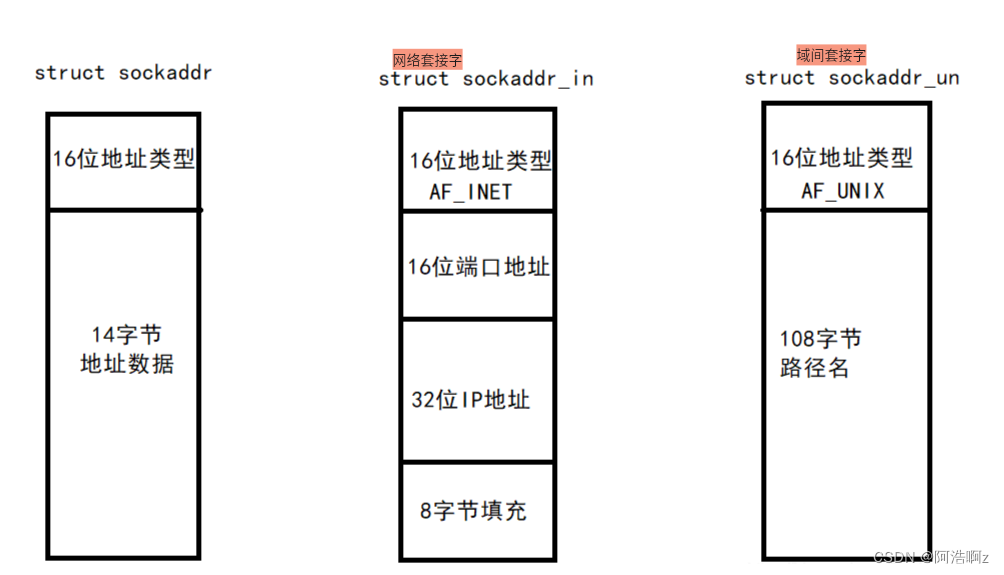
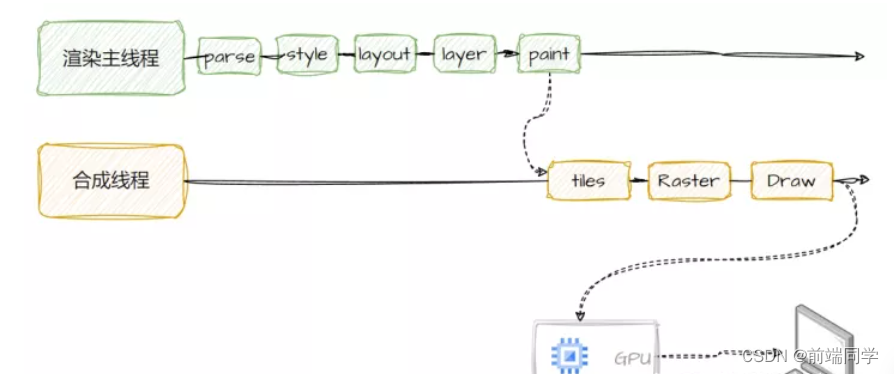
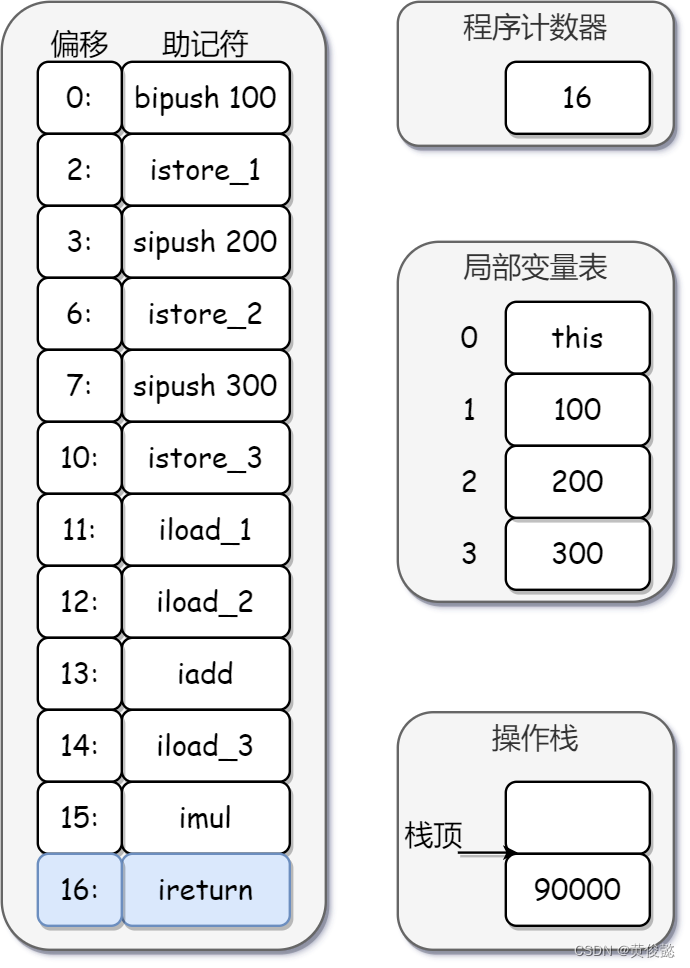
直方图均衡化(HE)

Histogram Equalization (HE)
设灰度水平在 $r_k,k\in [0，L-1]$ 内
一幅图像$f$ 的非归一化直方图定义为
$$h(r_k)=n_k$$

$$s=T(r)$$为转换后的灰度，要求函数T满足：
（1）区间内单调递增
（2）有$0\le T(r)\le L-1for0\le r\le L-1$
HE的数学表达
$$ifs=T(r)=(L-1){\int }_0^r{p}_r(w)dw$$$$then{p}_s(s)=\frac{1}{L-1}$$
采用累积分布函数（CDF）作为HE变换函数

离散化表达形式：
$$s_k=T(r_k)=(L-1)\sum _{j=0}^k{p}_r(r_j)=(L-1)\sum _{j=0}^k\frac{n_j}{n}$$

例子

均衡化前后直方图比较

小结：
（1）因为直方图是概率密度函数的近似，而且均衡化过程中不产生新的灰度级，所以直方图均衡化很少得到完全平坦的结果；
（2） 变换后灰度级减少，即出现灰度“简并”现象，造成一些灰度层次的损失。

matlab实现

H= imread('lena_gray.jpg');
%获取图片的尺寸 便于计算总像素数 即 m*n
[m,n]=size(H);
%生成一个一行 256 列的矩阵
p=zeros(1,256);
% 统计各灰度的像素个数
%find(H==i) 是在图像矩阵里面寻找灰度为 i 的点坐标
% 因为矩阵是从 1 开始的 所以为 p(i+1)
for i=0:255
	p(i+1)=length(find(H==i))/(m*n);
end
subplot(2,2,1);
imshow(H);
title('原图');
subplot(2,2,2);
% 显示原图的直方图
bar(0:255,p);
title('原图直方图');
% 利用循环 累加概率值
s=zeros(1,256);
for i=1:256
	for j=1:i
		s(i)=p(j)+s(i);
	end
end
%对 s 中的数先乘以 255，再取整
a=round(s*255);
b=H;
%更新原图像的灰度
for i=0:255
	b(find(H==i))=a(i+1);
end
subplot(2,2,3);
imshow(b)
title('均衡化后图像');
%统计更新后的概率
for i=0:255
	GPeq(i+1)=sum(p(find(a==i)));
end
subplot(2,2,4);
bar(0:255,GPeq); title('均衡化后的直方图');

直方图匹配（规定化）HS

Histogram specification (matching)

考察使输入图像的直方图均衡化的变换函数：$T(r):r\to s$
$$s=T(r)=(L-1){\int }_0^r{p}_r(w)dw$$
考察使输出图像的直方图均衡化的变换函数：$G(z):z\to s$
$$G(z)=(L-1){\int }_0^z{p}_z(t)dt=s$$
则$z=G^{-1}(s)=G^{-1}[T(r)]$
离散形式：
$s_k=T(r_k)=(L-1)\sum _{j=0}^k{p}_r(r_j)$
$z_k=G^{-1}(s_k)=G^{-1}(T(r_k))$




##备注：直方图规定化的代码后面有空再补充