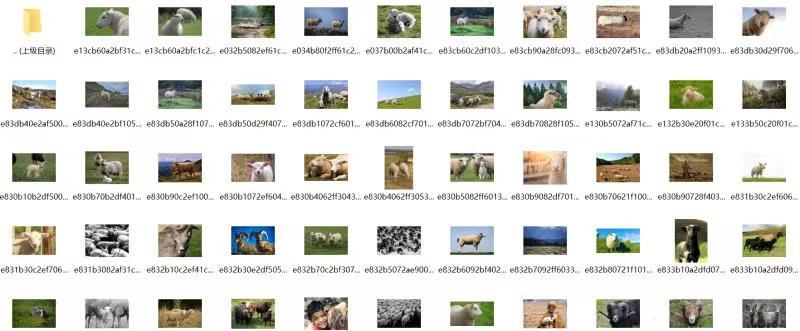
牛顿迭代法解超越方程
$$L=\frac{g{T}^2}{2\pi }tanh(\frac{2\pi }{L}d)$$

方程：

$$f(L)=L-\frac{g{T}^2}{2\pi }tanh(\frac{2\pi }{L}d)=0$$

导数为：
$$f^{{}^{\prime }}(L)=1-\frac{g{T}^{2}d}{L^{2}cos{h}^2(\frac{2\pi }{L}d)}$$

原理：

代码：

# 函数表达式x^3-2x+1
def fun(L):
    return L-9.8*10**2/(2*np.pi)*np.tanh(2*np.pi/L*40)
 
# 函数一阶导3x^2-2
def fun2(L):
    return 1+9.8*10**2*40*(1/np.cosh(2*np.pi*40/L))**2/(L**2)

# 迭代，参数：初始值、最大迭代次数、最小误差
def get_root(x0, max_iter=30, tol=1e-2):
    # 初始值浮点化
    p0 = x0 * 1.0
    # 最大50次迭代循环
    for i in range(max_iter):
        # 函数的一阶导不能为0，最普遍的说法是不能非正定
        p = p0 - fun(p0) / fun2(p0)
        # print(p)
        # 如果小于误差精度值则退出迭代
        if abs(p - p0) < tol:
            return "经过{}次迭代，我们估计的参数值是{}".format(i + 1, p)
        # 赋值重新迭代
        p0 = p
    print("无法迭代")
if __name__ == '__main__':
    print(get_root(200))
#     print(get_root(0))
#     print(get_root(-2))

输出：

经过3次迭代，我们估计的参数值是146.25131148928313