这篇文章是ICLR‘ 2022的一篇文章。
| No. | content |
|---|---|
| PAPER | {ICLR’ 2022} VOS: Learning What You Don’t Know by Virtual Outlier Synthesis |
| URL | 论文地址 |
| CODE | 代码地址 |
Motivation
· 现有OOD Detection方法大多依赖于真实的离群点数据集进行模型正则化,实际应用中过于昂贵,有时不可行。
· 作者认为导致OOD data效果差,主要是因为训练过程中缺少未知的知识,只在ID data上训练产生的决策边界对OOD Detection来说可能很糟糕。如图1-b所示,只用ID训练出来的分类器overconfident于远离ID data的区域(红色阴影部分),增加了OOD Detection的难度。作者认为模型应该学习一个更紧凑的决策边界,对于ID data应该有更低的不确定性,对OOD data有高的不确定性,如图1-c所示。
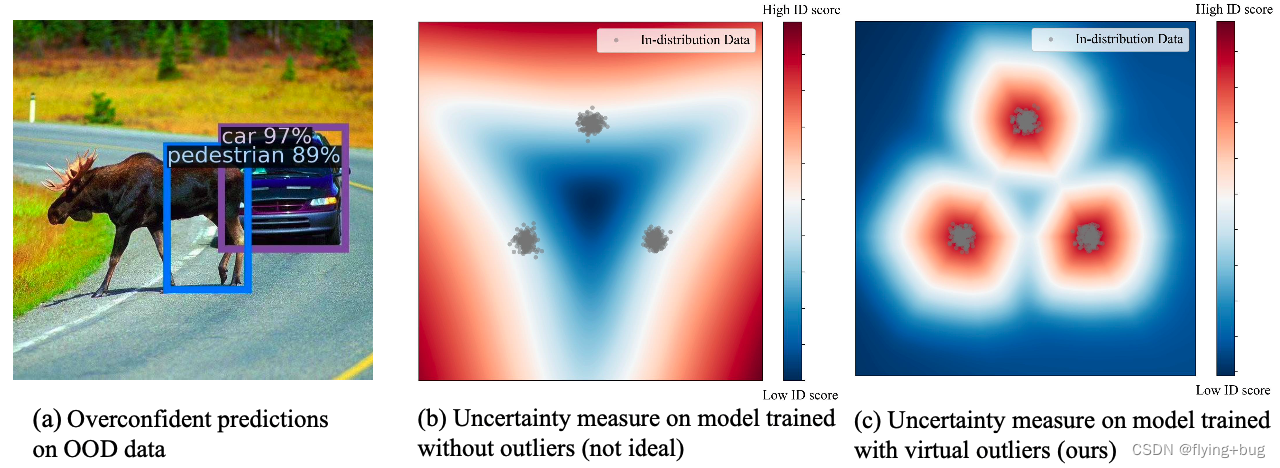
Contribution
· 提出了新的框架VOS,实现了SOTA
· VOS在feature space生成outliers的方式要比其他方法直接在高维像素空间生成的效果要好(e.g., using GAN (Lee et al., 2018a)),也优于直接使用噪声作为outliers的方法。
· 在常见的OOD Detection的benchmarks上测试了方法,还测试了一些目标检测任务。
Method

· 1. virtual outliers generation
假设特征表示满足多元类条件高斯分布:
p
θ
(
h
(
x
,
b
)
∣
y
=
k
)
=
N
(
μ
k
,
∑
)
p_{\theta}(h(x,\mathbb{b})|y=k)=\mathcal{N}(\mu_{k},\sum)
pθ(h(x,b)∣y=k)=N(μk,∑)
提取倒数第二层网络的特征,计算当前训练样本的
μ
^
k
\hat{\mu}_k
μ^k和
∑
^
\hat{\sum}
∑^
μ
^
k
=
1
N
k
∑
i
:
y
i
=
k
h
(
x
I
,
b
I
)
\hat{\mu}_k=\frac{1}{N_k}\sum_{i:y_i=k}h(x_I,b_I)
μ^k=Nk1i:yi=k∑h(xI,bI)
∑
^
=
1
N
∑
k
∑
i
:
y
i
=
k
(
h
(
x
i
,
b
i
)
−
μ
^
k
)
(
h
(
x
i
,
b
i
)
−
μ
^
k
)
T
\hat{\sum}=\frac{1}{N}\sum_{k}\sum_{i:y_i=k}(h(x_i,b_i)-\hat{\mu}_k)(h(x_i,b_i)-\hat{\mu}_k)^{T}
∑^=N1k∑i:yi=k∑(h(xi,bi)−μ^k)(h(xi,bi)−μ^k)T
得到高斯分布后,从特征空间采样outliers,
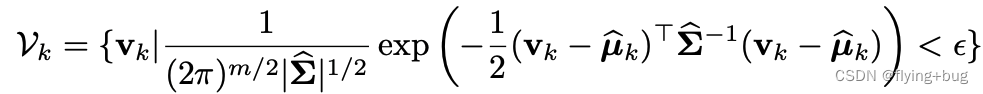
其中,
ϵ
\epsilon
ϵ应该足够小,保证采样的点很靠近类边界。
· 2. uncertainty Loss
Follow Liu et al., 2020a的思路,作者基于Energy-based model在OOD Detection uncertainty measurement优秀效果的启发,设计了uncertainty Loss。思路其实就是让ID data有更低的energy,outliers有更高的能量,作者这里直接让其分别为正值和负值了。
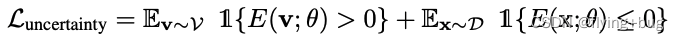
进一步,得到平滑近似版本
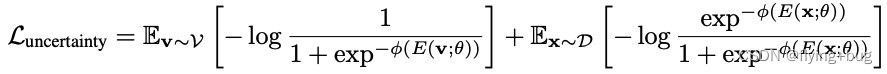
相比于Liu et al., 2020a的方法,作者认为他的方法不用再设置in- and out- of distribution data的超参阈值,效果更好。
最后总的training objective如下,
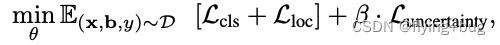
· 3. virtual outliers generation
在inference过程中,使用逻辑回归不确定性分支的输出进行OOD Detection。给定输入
x
∗
x^{*}
x∗,object detector产生
b
∗
b^{*}
b∗。OOD Detection的不确定性分数为
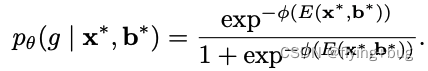
设置阈值区分ID和OOD目标
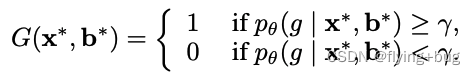
VOS整体framework:

Reference
Weitang Liu, Xiaoyun Wang, John Owens, and Yixuan Li. Energy-based out-of-distribution detection. Advances in Neural Information Processing Systems, 2020a.
Du X, Wang Z, Cai M, et al. VOS: Learning What You Don’t Know by Virtual Outlier Synthesis[C]//International Conference on Learning Representations.