前言：

算法训练系列是做《代码随想录》一刷，个人的学习笔记和详细的解题思路，总共会有60篇博客来记录，计划用60天的时间刷完。

内容包括了面试常见的10类题目，分别是：数组，链表，哈希表，字符串，栈与队列，二叉树，回溯算法，贪心算法，动态规划，单调栈。

博客记录结构上分为思路，代码实现，复杂度分析，思考和收获，四个方面。

如果这个系列的博客可以帮助到读者，就是我最大的开心啦，一起LeetCode一起进步呀；）

LeetCode1005.K次取反后最大化的数组和

1. 思路

2. 代码实现

3. 复杂度分析

4. 思考与收获

Leetcode134. 加油站

方法一：暴力解法

1. 思路

2. 代码实现

3. 复杂度分析

4. 思考与收获

方法二：宏观的贪心算法

1. 思路

2. 代码实现

3. 复杂度分析

4. 思考与收获

方法三：贪心解法

1. 思路

2. 代码实现

3. 复杂度分析

4. 思考与收获

总结

Leetcode135. 分发糖果

1. 思路

2. 代码实现

3. 复杂度分析

4. 思考与收获

LeetCode1005.K次取反后最大化的数组和

链接：1005. K 次取反后最大化的数组和 - 力扣（LeetCode）

1. 思路

本题思路其实比较好想了，如何可以让数组和最大呢？

贪心的思路，局部最优：让绝对值大的负数变为正数，当前数值达到最大，整体最优：整个数组和达到最大。

局部最优可以推出全局最优。

那么如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让数组和达到最大。

那么又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比反转5得到的-5 大多了），全局最优：整个数组和达到最大。

虽然这道题目大家做的时候，可能都不会去想什么贪心算法，一鼓作气，就AC了。

我这里其实是为了给大家展现出来经常被大家忽略的贪心思路，这么一道简单题，就用了两次贪心！

那么本题的解题步骤为：

第一步：将数组按照绝对值大小从大到小排序，注意要按照绝对值的大小
第二步：从前向后遍历，遇到负数将其变为正数，同时K--
第三步：如果K还大于0，那么反复转变数值最小的元素，将K用完
第四步：求和

2. 代码实现

# time:O(NlogN);space:O(N)
class Solution(object):
    def largestSumAfterKNegations(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: int
        """
        # 将数组nums按照绝对值大小，从大到小排序
        sortedNums = sorted(nums,key=abs,reverse=True)
        index = 0
        # 从大的开始，把负数变成正数
        while k>0 and index<len(nums):
            if sortedNums[index]<0:
                sortedNums[index] *= -1
                k -= 1
            index += 1
        # 如果所有数都变成非负数之后，K仍为正数
        # 就针对最后一个绝对值最小的数，把K都用完
        if k>0:
            sortedNums[-1] *= (-1)**k
        return sum(sortedNums)

3. 复杂度分析

时间复杂度：O(logN）

其中N为数组nums的长度，首先需要对数组nums进行排序的时间复杂度为O(NlogN）；然后需要遍历一遍数组，从大到小把尽可能多的负数变成正数，O（N），还有sum操作，复杂度O(N），总体时间复杂度O(NlogN）；
空间复杂度：O(N）

其中N为nums的长度，sorted排序新建了一个数组，O(N)；

4. 思考与收获

空间复杂度上还可以继续优化，不用sorted，而用sort，就会在原数组上进行操作，不会新建一个数组，复杂度可以降低为O(1），代码如下：

# time:O(NlogN);space:O(1)
class Solution(object):
    def largestSumAfterKNegations(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: int
        """
        # 将数组nums按照绝对值大小，从大到小排序
        nums.sort(key=abs,reverse=True)
        index = 0
        # 从大的开始，把负数变成正数
        while k>0 and index<len(nums):
            if nums[index]<0:
                nums[index] *= -1
                k -= 1
            index += 1
        # 如果所有数都变成非负数之后，K仍为正数
        # 就针对最后一个绝对值最小的数，把K都用完
        if k>0:
            nums[-1] *= (-1)**k
        return sum(nums)

贪心的题目如果简单起来，会让人简单到开始怀疑：本来不就应该这么做么？这也算是算法？我认为这不是贪心？本题其实很简单，不会贪心算法的同学都可以做出来，但是我还是全程用贪心的思路来讲解。因为贪心的思考方式一定要有！如果没有贪心的思考方式（局部最优，全局最优），很容易陷入贪心简单题凭感觉做，贪心难题直接不会做，其实这样就锻炼不了贪心的思考方式了。所以明知道是贪心简单题，也要靠贪心的思考方式来解题，这样对培养解题感觉很有帮助！

Reference：代码随想录 (programmercarl.com)

本题学习时间：30分钟。

Leetcode134. 加油站

链接：134. 加油站 - 力扣（LeetCode）

方法一：暴力解法

1. 思路

遍历每一个加油站为起点的情况，模拟一圈；

如果跑了一圈，中途没有断油，而且最后油量大于等于0，说明这个起点是ok的

2. 代码实现

# 解法一： 暴力解法
# Python 会超时
# time:O(N^2);space:O(1)
class Solution(object):
    def canCompleteCircuit(self, gas, cost):
        """
        :type gas: List[int]
        :type cost: List[int]
        :rtype: int
        """
        # 每个起点都尝试一遍
        for i in range(len(cost)):
            # 先走到i的下一步
            # 记录剩余的油量
            rest = gas[i] - cost[i]
            index = (i+1)%len(cost)
            # 模拟以i为起点跑下剩余的一圈
            while rest>0 and index!=i:
                rest += gas[index]-cost[index]
                index = (index+1)%len(cost)
            # 如果以i为起点跑一圈，剩余油量>=0，返回该起始位置
            if rest>=0 and index==i: return i 
        return -1

3. 复杂度分析

时间复杂度：O(N^2)

其中N为加油站的个数，也是gas数组和cost数组的长度，需要以每个加油站为起点，模拟跑圈跑一遍，所以时间复杂度为O(N^2)；
空间复杂度：O(1）

只有常数个变量来记录；

4. 思考与收获

for循环适合模拟从头到尾的遍历，而while循环适合模拟环形遍历，要善于使用while；
暴力的方法思路比较简单，但代码写起来也不是很容易，关键是要模拟跑一圈的过程。

方法二：宏观的贪心算法

1. 思路

直接从全局进行贪心选择，情况如下：

情况一：如果gas的总和小于cost总和，那么无论从哪里出发，一定是跑不了一圈的
情况二：rest[i] = gas[i]-cost[i]为一天剩下的油，i从0开始计算累加到最后一站，如果累加没有出现负数，说明从0出发，油就没有断过，那么0就是起点。
情况三：如果累加的最小值是负数，汽车就要从非0节点出发，从后向前，看哪个节点能这个负数填平，能把这个负数填平的节点就是出发节点。

2. 代码实现

# 解法二：宏观贪心
# time:O(N);space:O(1)
class Solution(object):
    def canCompleteCircuit(self, gas, cost):
        """
        :type gas: List[int]
        :type cost: List[int]
        :rtype: int
        """
        totalSum = 0
        totalMin = float("inf")
        n = len(gas)
        for i in range(n):
            totalSum += gas[i]-cost[i]
            totalMin = min(totalMin,totalSum)
        if totalSum<0: return -1
        if totalMin>=0: return 0
        for j in range(n-1,-1,-1):
            totalMin += gas[j]-cost[j]
            if totalMin >=0: return j

3. 复杂度分析

时间复杂度：O(N）

从头到尾遍历数组不超过两遍，所以O(N)；
空间复杂度：O（1）；

只有常数个变量需要保存；

4. 思考与收获

**其实Carl不认为这种方式是贪心算法，因为没有找出局部最优，而是直接从全局最优的角度上思考问题。**但这种解法又说不出是什么方法，这就是一个从全局角度选取最优解的模拟操作，但不管怎么说，解法毕竟还是巧妙的，不用过于执着于其名字称呼。

方法三：贪心解法

1. 思路

可以换一个思路，首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈，说明各个站点的加油站剩油量rest[i]相加一定是大于等于零的。

每个加油站的剩余量rest[i]为gas[i] - cost[i]。

i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明[0, i]区间都不能作为起始位置，起始位置从i+1算起，再从0计算curSum。

如图：

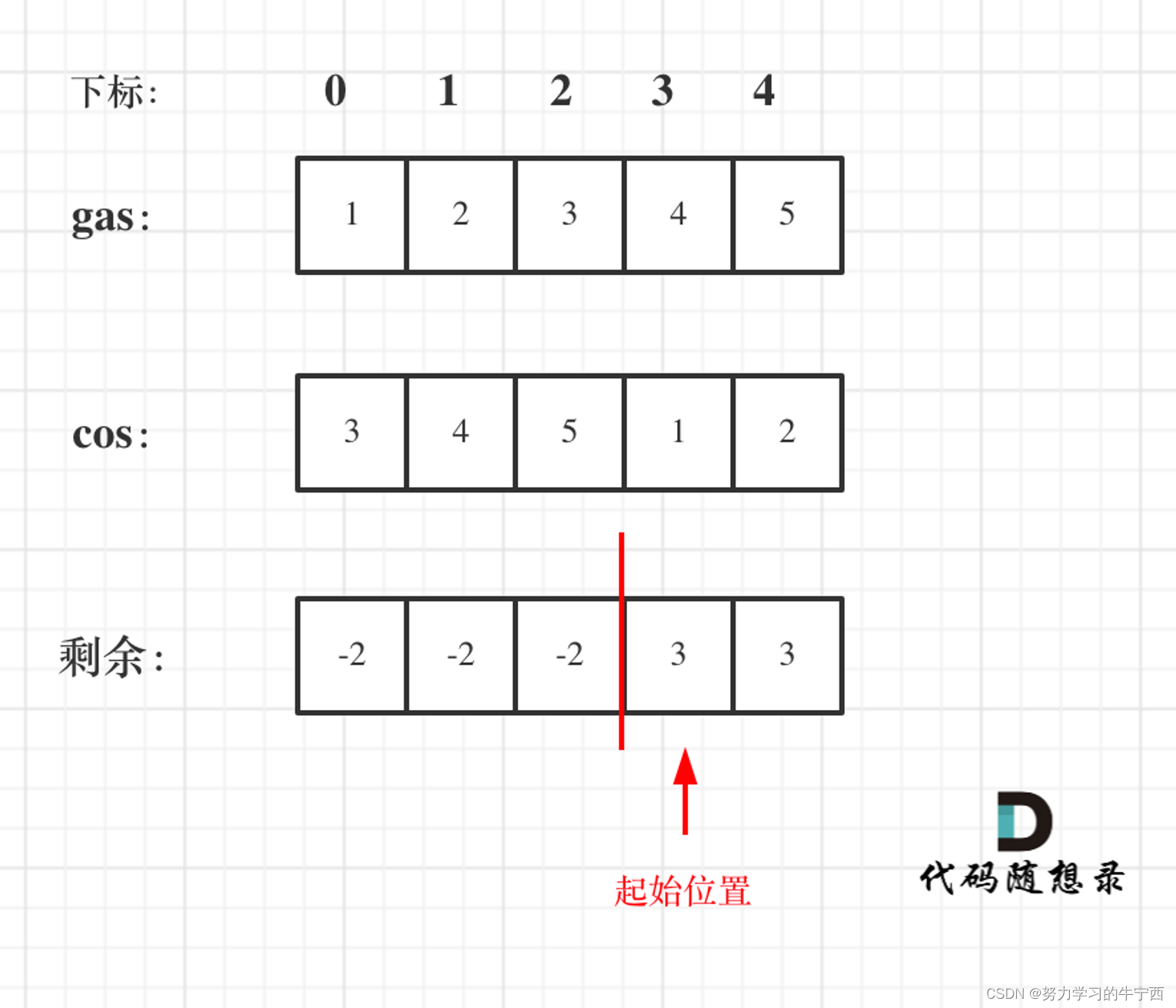
那么为什么一旦[i，j] 区间和为负数，起始位置就可以是j+1呢，j+1后面就不会出现更大的负数？

如果出现更大的负数，就是更新j，那么起始位置又变成新的j+1了。

而且j之前出现了多少负数，j后面就会出现多少正数，因为耗油总和是大于零的（前提我们已经确定了一定可以跑完全程）。

那么局部最优：当前累加rest[j]的和curSum一旦小于0，起始位置至少要是j+1，因为从j开始一定不行。全局最优：找到可以跑一圈的起始位置。

局部最优可以推出全局最优，找不出反例，试试贪心！

2. 代码实现

# 方法三： 贪心算法
# time:O(N);space:(1)
class Solution(object):
    def canCompleteCircuit(self, gas, cost):
        """
        :type gas: List[int]
        :type cost: List[int]
        :rtype: int
        """
        start = 0
        curSum = 0
        totalSum = 0
        n = len(gas)
        for i in range(n):
            curSum += gas[i] - cost[i]
            totalSum += gas[i] -cost[i]
            # 当前累加rest[i]和 curSum一旦小于0
            if curSum<0:
                # 起始位置更新为i+1,curSum从0开始
                curSum = 0
                start = i+1
        # 说明怎么走都不可能跑一圈了
        if totalSum<0: return -1
        return start

3. 复杂度分析

时间复杂度：O(N）

从头到尾遍历数组，所以O(N)；
空间复杂度：O（1）；

只有常数个变量需要保存；

4. 思考与收获

说这种解法为贪心算法，才是是有理有据的，因为全局最优解是根据局部最优推导出来的；

总结

对于本题首先给出了暴力解法，暴力解法模拟跑一圈的过程其实比较考验代码技巧的，要对while使用的很熟练；
然后给出了两种贪心算法，对于第一种贪心方法，其实我认为就是一种直接从全局选取最优的模拟操作，思路还是好巧妙的，值得学习一下；
对于第二种贪心方法，才真正体现出贪心的精髓，用局部最优可以推出全局最优，进而求得起始位置。

Reference：代码随想录 (programmercarl.com)

本题学习时间：60分钟。

Leetcode135. 分发糖果

链接：135. 分发糖果 - 力扣（LeetCode）

1. 思路

这道题目一定是要确定一边之后，再确定另一边，例如比较每一个孩子的左边，然后再比较右边，如果两边一起考虑一定会顾此失彼；

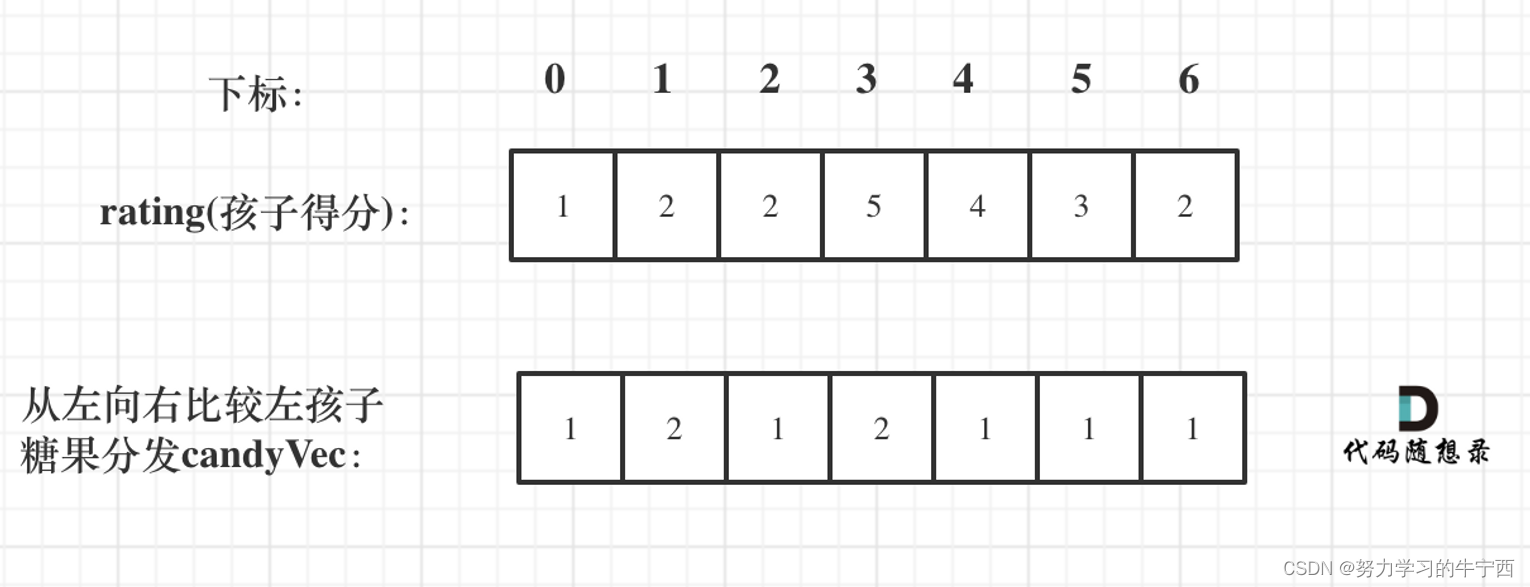
💡 先确定右边评分大于左边的情况（也就是从前向后遍历）

此时局部最优：只要右边评分比左边大，右边的孩子就多一个糖果
全局最优：相邻的孩子中，评分高的右孩子获得比左边孩子更多的糖果；局部最优可以推出全局最优。

如果ratings[i] > ratings[i - 1] 那么[i]的糖一定要比[i - 1]的糖多一个，所以贪心：candyVec[i] = candyVec[i - 1] + 1

如图：

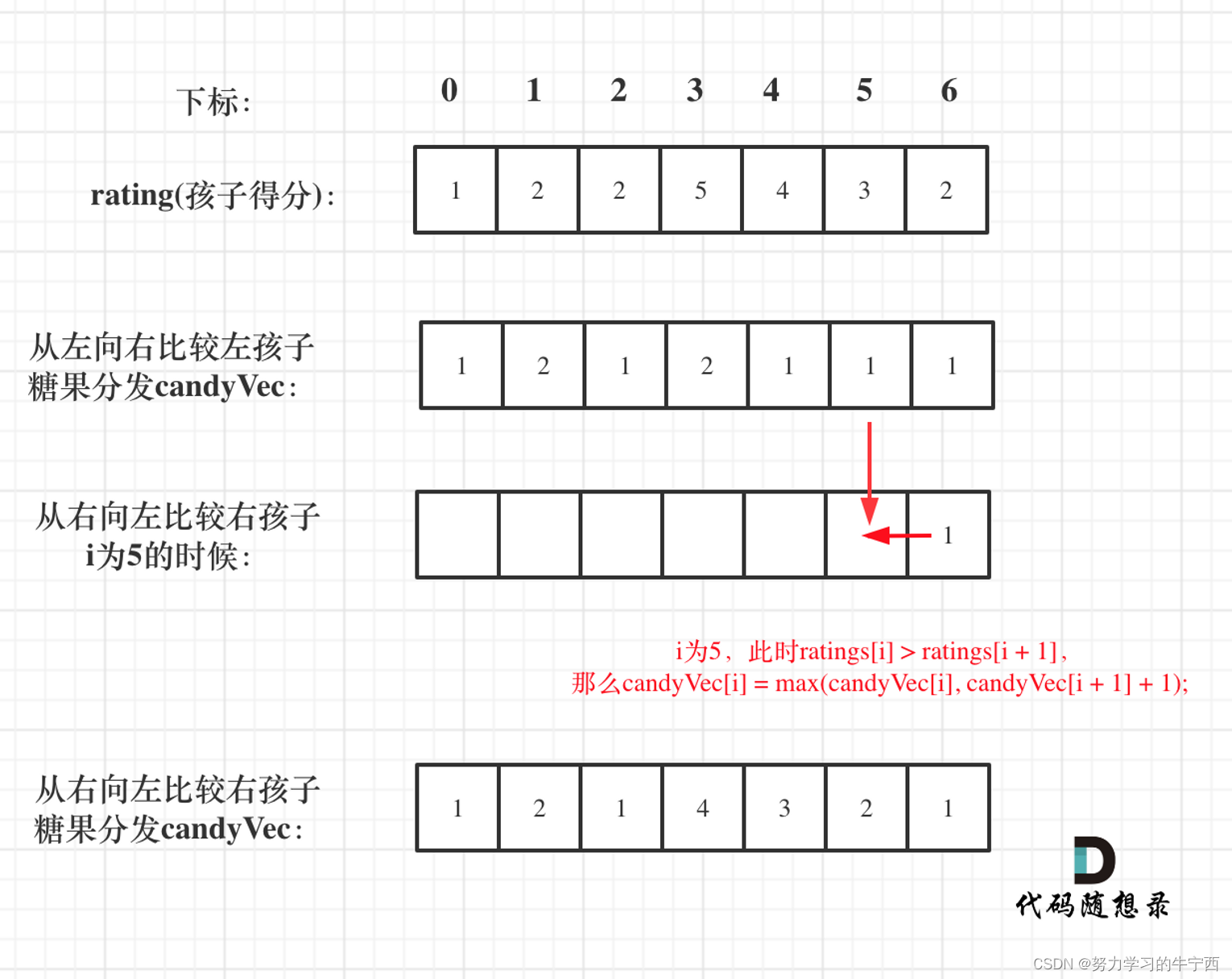
💡 再确定左孩子大于右孩子的情况（从后向前遍历）

遍历顺序这里有同学可能会有疑问，为什么不能从前向后遍历呢？

因为如果从前向后遍历，根据 ratings[i + 1] 来确定 ratings[i] 对应的糖果，那么每次都不能利用上前一次的比较结果了；

所以确定左孩子大于右孩子的情况一定要从后向前遍历！

如果 ratings[i] > ratings[i + 1]，此时candyVec[i]（第i个小孩的糖果数量）就有两个选择了，一个是candyVec[i + 1] + 1（从右边这个加1得到的糖果数量），一个是candyVec[i]（之前比较右孩子大于左孩子得到的糖果数量）。

那么又要贪心了，局部最优：取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，保证第i个小孩的糖果数量即大于左边的也大于右边的。全局最优：相邻的孩子中，评分高的孩子获得更多的糖果。

局部最优可以推出全局最优。

所以就取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多，也比右边candyVec[i + 1]的糖果多。

2. 代码实现

# 贪心算法
# time:O(N);space:O(N)
class Solution(object):
    def candy(self, ratings):
        """
        :type ratings: List[int]
        :rtype: int
        """
        candy = [1]*len(ratings)
        # 从前向后
        for i in range(1,len(ratings)):
            if ratings[i]>ratings[i-1]:
                candy[i] = candy[i-1]+1
        # 从后向前
        for i in range(len(ratings)-2,-1,-1):
            if ratings[i]>ratings[i+1]:
                candy[i] = max(candy[i],candy[i+1]+1)
        return sum(candy)

3. 复杂度分析

时间复杂度：O(N）

其中N为数组ratings的长度，也为孩子的个数；本解法需要从左到右遍历一遍，再从右向左遍历一遍，还需要sum数组candy，总的时间复杂度O(N)；
空间复杂度：O(N)

其中N为数组ratings的长度，也为孩子的个数；需要新建一个数组candy来记录每个孩子的糖果数；

4. 思考与收获

这在leetcode上是一道困难的题目，其难点就在于贪心的策略，如果在考虑局部的时候想两边兼顾，就会顾此失彼；
那么本题我采用了两次贪心的策略：
- 一次是从左到右遍历，只比较右边孩子评分比左边大的情况。
- 一次是从右到左遍历，只比较左边孩子评分比右边大的情况。
这样从局部最优推出了全局最优，即：相邻的孩子中，评分高的孩子获得更多的糖果。

Reference: 代码随想录 (programmercarl.com)

本题学习时间：60分钟。

本篇学习时间近3小时，总结字数6000+；本篇学习了三道贪心算法的题目，第一题相对简单，甚至写完了都不知道自己用了贪心算法的思路，要刻意训练自己这种意识，第二题的贪心思路不太好想，重点是方法二，第三题是不能同时两头兼顾，必须一边一边处理。（求推荐！）