1.八大排序
加一个计数排序(时间复杂度为O(n), 空间复杂度为O(max(n, range),非比较排序)。
2.希尔排序

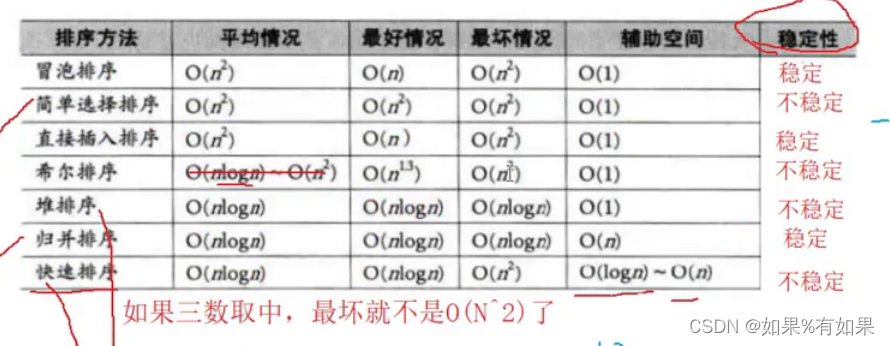
3.三个O(n^2)的排序的比较

4.归并排序和快速排序
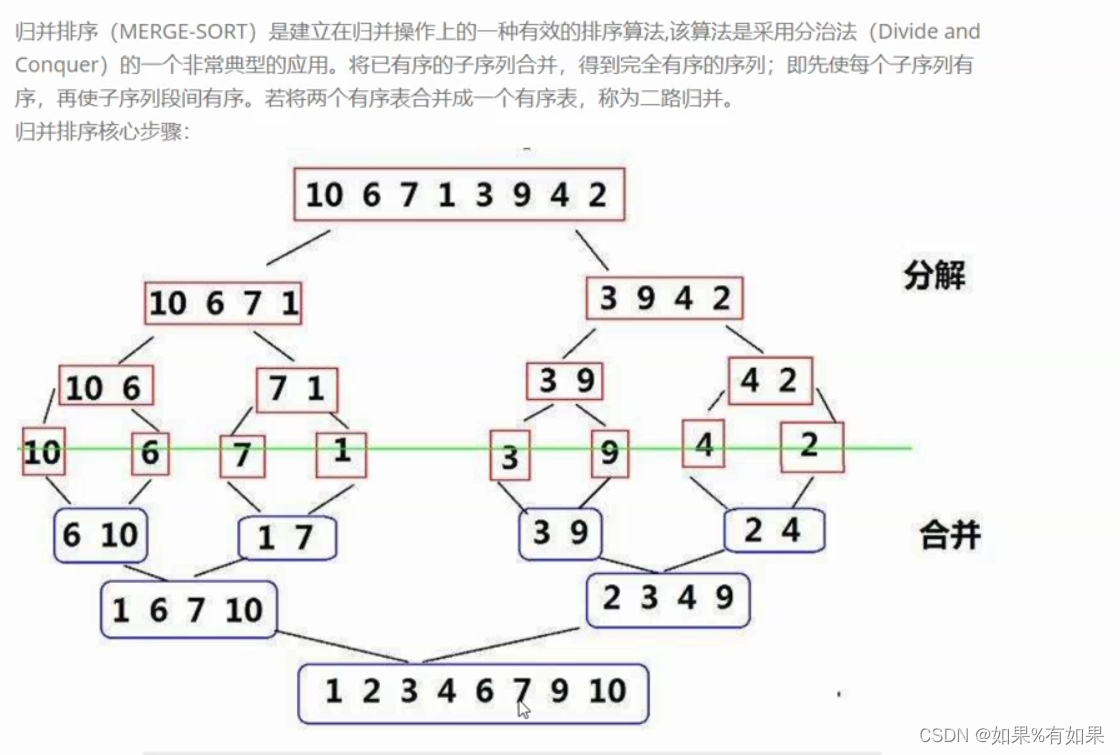
非递归:


5.排序比较
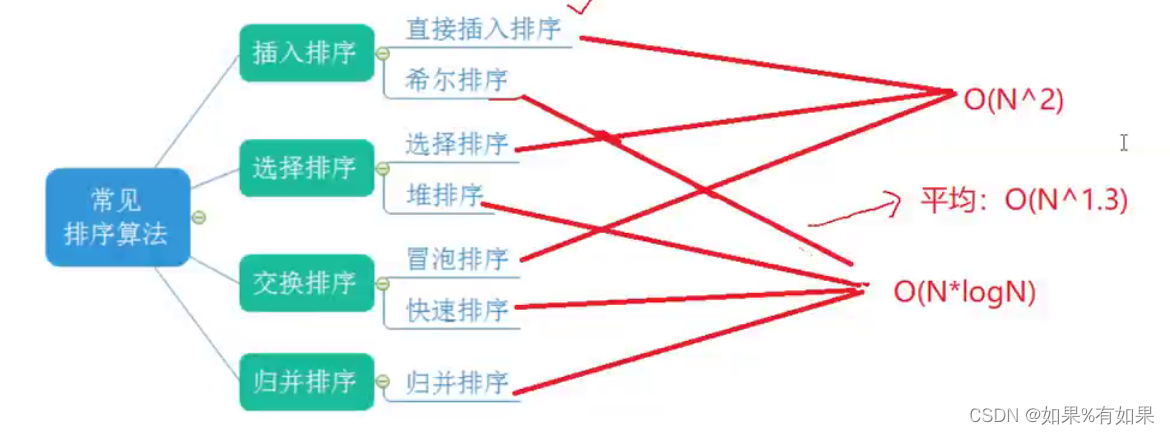
注意: 下面4种高效排序中,综合性能最好的是快速排序,但是在全都是一个相同的数的情况下,快排的效率最低,因为它无法分成大小区间,在实际中,希尔排序用的比较少,它是数据越多,越无序,优势越明显,但是面对少量数据优势就变成了劣势,归并排序空间复杂度较高,堆排序要先建堆,精确的时间复杂度是O(n + nlogn)。具体效率见下图:
1.1 十万个随机数Debug模式下:

1.2 十万个随机数Release模式下:

2.1 百万个随机数Debug模式下:

2.2 百万个随机数Release模式下:

3.1 千万个随机数Debug模式下:

3.2 千万个随机数Release模式下:

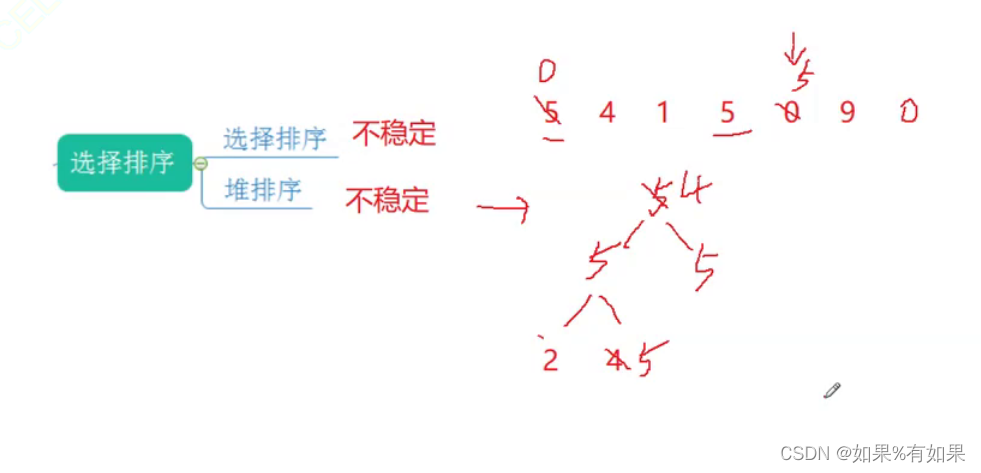
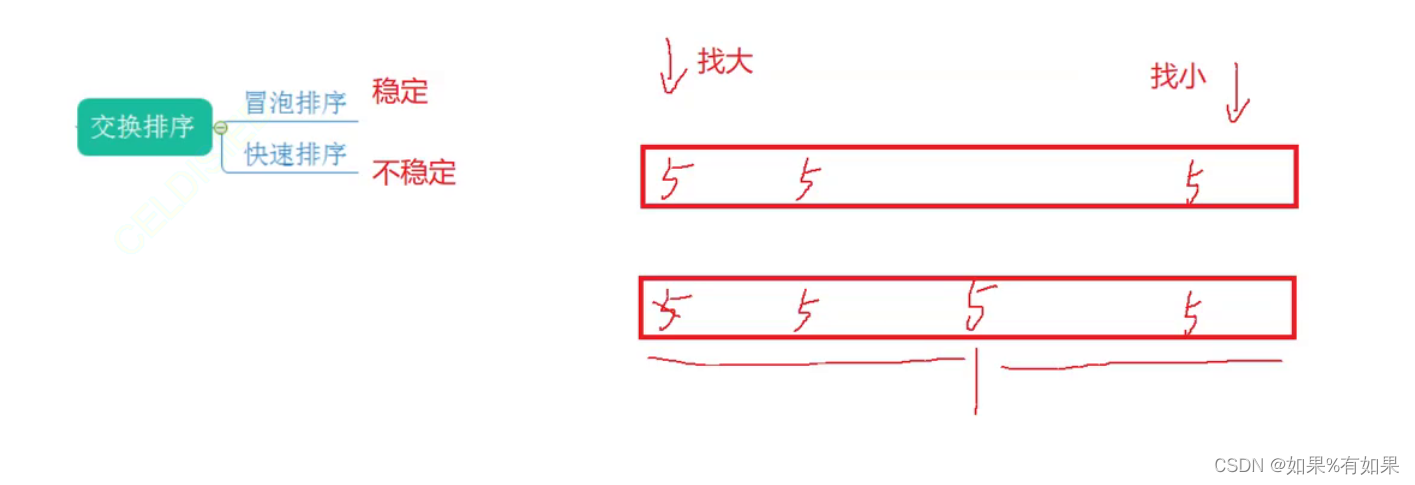
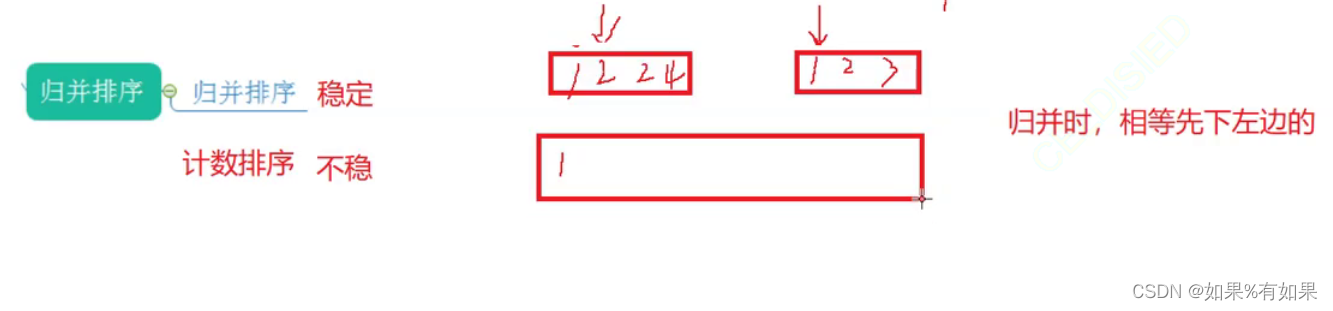
6.稳定型:
数组中相同的值,在排序之后相对位置是否变化,如果可能会变,就是不稳定的,不变就是稳定的。
所有的排序都可以不稳定。

7.堆排序参考以下博客:
4.6.2二叉树(堆和堆排序)(C语言)
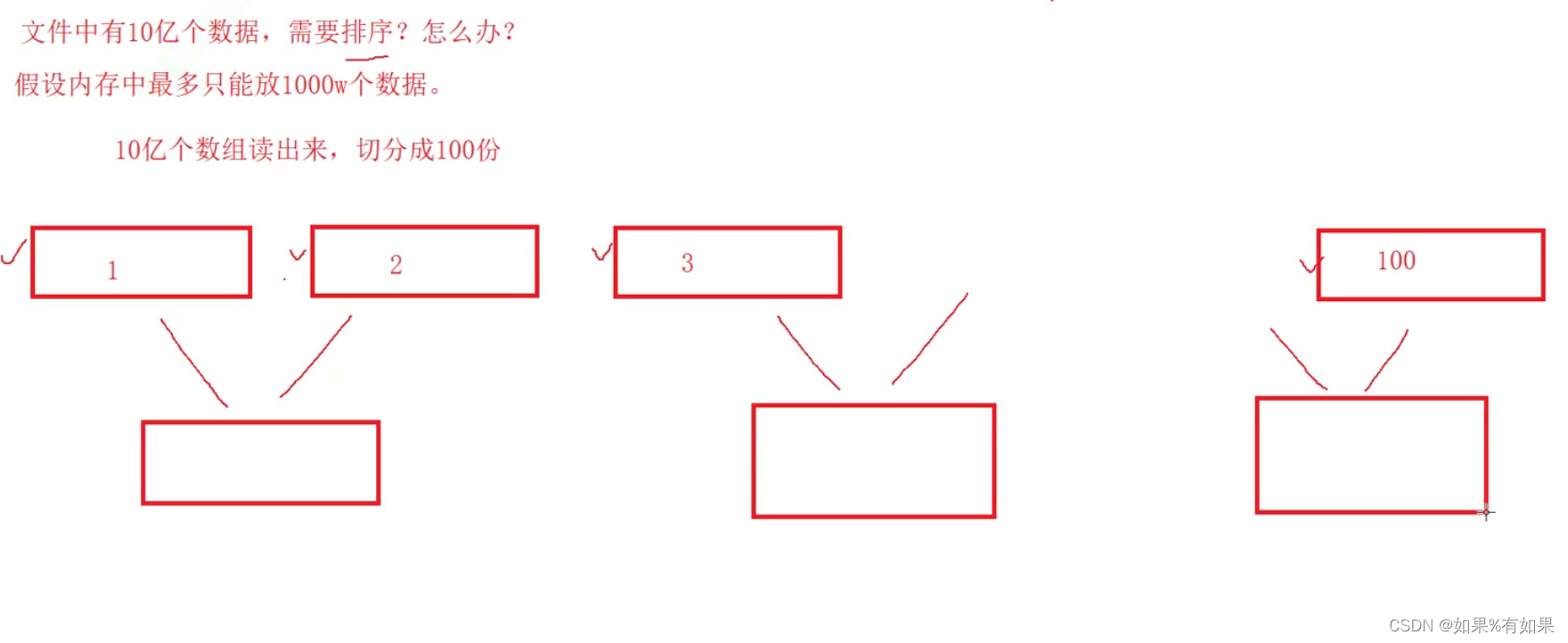
8.内排序和外排序
9.我的代码:
#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int STDataType; //重定义数据类型
typedef struct Stack
{
STDataType* data;
int top; //栈顶
int capacity; //容量
}Stack;
extern void StackInit(Stack* ps); // 1.初始化栈
extern void StackPush(Stack* ps, STDataType x); // 2.入栈
extern void StackPop(Stack* ps); // 3.出栈
extern STDataType StackTop(Stack* ps); // 4.获取栈顶元素
extern int StackSize(Stack* ps); // 5.获取栈中有效元素个数
extern bool StackEmpty(Stack* ps); // 6.检测栈是否为空
extern void StackDestroy(Stack* ps); // 7.销毁栈 #include"Stack.h"
void StackInit(Stack* ps) // 1.初始化栈
{
assert(ps);
ps->data = NULL;
ps->capacity = 0;
ps->top = 0; //初始值是-1或0都可以,但是初始值不同,后期的操作不同
}
void StackPush(Stack* ps, STDataType x) // 2.入栈
{
assert(ps);
if (ps->capacity == ps->top) //扩容
{
int newcapacity = ps->capacity > 0 ? 2 * ps->capacity : 4; //考虑容量为0的情况
STDataType* tmp = (STDataType*)realloc(ps->data, sizeof(STDataType) * newcapacity);
if (tmp == NULL) //考虑扩容失败
{
perror("realloc:");
return;
}
ps->data = tmp;
ps->capacity = newcapacity;
}
ps->data[ps->top] = x;
ps->top++;
}
void StackPop(Stack* ps) // 3.出栈
{
assert(ps);
assert(!StackEmpty(ps)); //考虑栈空
ps->top--;
}
STDataType StackTop(Stack* ps) // 4.获取栈顶元素
{
assert(ps);
assert(!StackEmpty(ps)); //考虑栈空
return ps->data[ps->top - 1];
}
int StackSize(Stack* ps) // 5.获取栈中有效元素个数
{
assert(ps);
return ps->top;
}
bool StackEmpty(Stack* ps) // 6.检测栈是否为空
{
assert(ps);
return ps->top == 0;
}
void StackDestroy(Stack* ps) // 7.销毁栈
{
assert(ps);
free(ps->data);
ps->data = NULL;
ps->capacity = 0;
ps->top = 0;
}#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<windows.h>
#include<string.h>
typedef int dataType;
// 打印
extern void PrintArray(dataType* a, int n);
// 插入排序
extern void InsertSort(dataType* a, int n);
// 希尔排序
extern void ShellSort(dataType* a, int n);
// 选择排序
extern void SelectSort(dataType* a, int n);
// 冒泡排序
extern void BubbleSort(dataType* a, int n);
// 堆排序
extern void HeapSort(dataType* a, int n);
// 快速排序
extern void QuickSort(dataType* a, int left, int right);
// 快速排序非递归
extern void QuickSortNonR(dataType* a, int left, int right);
// 归并排序递归
extern void MergeSort(dataType* a, int n);
// 归并排序非递归
extern void MergeSortNonR(dataType* a, int n);
// 计数排序
extern void CountSort(dataType* a, int n);
#include"Sort.h"
#include"Stack.h"
//交换两个数
void swap(dataType* pa, dataType* pb)
{
int tmp = *pa;
*pa = *pb;
*pb = tmp;
}
// 打印
void PrintArray(dataType* a, int n)
{
assert(a);
for (int i = 0; i < n; ++i)
{
printf("%d ", a[i]);
}
printf("\n");
}
// 插入排序
void InsertSort(dataType* a, int n)
{
assert(a);
for (int i = 0; i < n - 1; ++i)
{
int end = i;
int x = a[end + 1];
while (end >= 0)
{
if (x < a[end])
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = x;
}
}
// 希尔排序
void ShellSort(dataType* a, int n)
{
int gap = n;
//多次预排
while (gap > 1)
{
//确保最后一次gap是1
//gap = gap / 3 + 1;
gap = gap / 2;
//一锅炖,一步到位
for (int i = 0; i < n - gap; i++)
{
int end = i;
int x = a[end + gap];
while (end >= 0)
{
if (x < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = x;
}
}
}
// 选择排序
void SelectSort(dataType* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int iMax = begin;
int iMin = end;
//记录最大和最小的位置
for (int i = begin; i <= end; ++i)
{
if (a[i] > a[iMax])
{
iMax = i;
}
if (a[i] < a[iMin])
{
iMin = i;
}
}
swap(&a[iMin], &a[begin]);
//考虑特殊情况,当最大值在第一个的时候,第一次交换会被换到最小值的位置
if (iMax == begin)
{
iMax = iMin;
}
swap(&a[iMax], &a[end]);
++begin;
--end;
}
}
//向下调整
void adjustDown(dataType* a, int n, int iParent)
{
//假设左孩子大
int iChild = iParent * 2 + 1;
while (iChild < n)
{
//如果右孩子大
if (iChild + 1 < n && a[iChild + 1] > a[iChild])
{
++iChild;
}
if (a[iChild] > a[iParent])
{
swap(&a[iChild], &a[iParent]);
iParent = iChild;
iChild = iParent * 2 + 1;
}
else
{
break;
}
}
}
// 堆排序
void HeapSort(dataType* a, int n)
{
//先建立一个堆
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
adjustDown(a, n, i);
}
//堆顶元素和最后一个元素交换,剩下的继续向下调整
int iEnd = n - 1;
while (iEnd != 0)
{
adjustDown(a, iEnd + 1, 0);
swap(&a[0], &a[iEnd]);
--iEnd;
}
}
// 冒泡排序
void BubbleSort(dataType* a, int n)
{
int end = n;
while (end > 0)
{
int flag = 0;
for (int j = 1; j < end; ++j)
{
if (a[j - 1] > a[j])
{
swap(&a[j - 1], &a[j]);
flag = 1;
}
}
if (flag == 0)
{
break;
}
--end;
}
}
//快排优化,三数取中
int getMidIndex(int* a, int left, int right)
{
int iMid = left + ((right - left) >> 1);
if (a[left] > a[iMid])
{
if (a[right] >= a[left])
{
return left;
}
else
{
return a[right] > a[iMid] ? right : iMid;
}
}
else //a[left] <= a[iMid]
{
if (a[right] >= a[iMid])
{
return iMid;
}
else
{
return a[left] > a[right] ? left : right;
}
}
}
// 一次快排,左右指针法
int partSort1(int* a, int left, int right)
{
//三数取中作为key
int mid = getMidIndex(a, left, right);
int iKey = left;
swap(&a[iKey], &a[mid]);
while (left < right)
{
//先从右边开始找小
while (left < right && a[iKey] <= a[right])
{
--right;
}
//再从左边找大
while (left < right && a[iKey] >= a[left])
{
++left;
}
//交换
swap(&a[left], &a[right]);
}
//最后和iKey位置交换
swap(&a[left], &a[iKey]);
return left;
}
//一次快排,挖坑法
int partSort2(int* a, int left, int right)
{
//三数取中作为key
int mid = getMidIndex(a, left, right);
int dig = left;
swap(&a[dig], &a[mid]);
//保存dig的值
int key = a[dig];
while (left < right)
{
//右边找小,和坑交换,并且作为新的坑
while (left < right && a[right] >= key)
{
--right;
}
a[dig] = a[right];
dig = right;
//左边找大,和坑交换,并且作为新的坑
while (left < right && a[left] <= key)
{
++left;
}
a[dig] = a[left];
dig = left;
}
a[dig] = key;
return dig;
}
//一次快排,前后指针法
int partSort3(int* a, int left, int right)
{
int mid = getMidIndex(a, left, right);
swap(&a[left], &a[mid]);
int cur = left + 1;
int prev = left;
while (cur <= right)
{
//方法1
/*while (cur <= right && a[cur] >= a[left])
{
++cur;
}
if (cur <= right)
{
++prev;
swap(&a[cur], &a[prev]);
++cur;
}*/
//方法2
if (a[cur] < a[left] && ++prev != cur)
{
swap(&a[cur], &a[prev]);
}
++cur;
}
swap(&a[prev], &a[left]);
return prev;
}
// 快速排序
void QuickSort(dataType* a, int left, int right)
{
if (left >= right)
{
return;
}
//小区间优化,使用直接插入排序
if (right - left + 1 < 10)
{
InsertSort(a + left, right - left + 1);
}
//定义中间位置iKey
int iKey = partSort3(a, left, right);
//处理中间位置的左边
QuickSort(a, left, iKey - 1);
QuickSort(a, iKey + 1, right);
}
// 快速排序非递归
void QuickSortNonR(dataType* a, int left, int right)
{
//使用栈存储区间
Stack st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (!StackEmpty(&st))
{
int end = StackTop(&st);
//注意出栈的顺序
StackPop(&st);
int begin = StackTop(&st);
StackPop(&st);
int iKey = partSort3(a, begin, end);
//[begin, iKey - 1] iKey [iKey + 1, end]
if (iKey + 1 < end)
{
StackPush(&st, iKey + 1);
StackPush(&st, end);
}
if (begin < iKey - 1)
{
StackPush(&st, begin);
StackPush(&st, iKey - 1);
}
}
StackDestroy(&st);
}
//归并排序递归法
void _MergeSort(dataType* a, int left, int right, dataType* tmp)
{
if (left >= right)
{
return;
}
int mid = (left + right) / 2;
//[left, mid] [mid + 1, right]
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid + 1, right, tmp);
int begin1 = left;
int end1 = mid;
int begin2 = mid + 1;
int end2 = right;
int i = left;
//比较,将小的放入临时数组中
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i] = a[begin1];
i++;
begin1++;
}
else
{
tmp[i] = a[begin2];
i++;
begin2++;
}
}
//处理尾巴
//以下两个循环只会进一个
while (begin1 <= end1)
{
tmp[i] = a[begin1];
i++;
begin1++;
}
while (begin2 <= end2)
{
tmp[i] = a[begin2];
i++;
begin2++;
}
//将tmp数组中的有序数组拷贝回原数组
for (int j = left; j <= right; j++)
{
a[j] = tmp[j];
}
}
// 归并排序
void MergeSort(dataType* a, int n)
{
dataType* tmp = (dataType*)malloc(sizeof(dataType) * n);
if (tmp == NULL)
{
perror("malloc:");
exit(-1);
}
int left = 0;
int right = n - 1;
_MergeSort(a, left, right, tmp);
free(tmp);
tmp = NULL;
}
// 归并排序非递归
void MergeSortNonR(dataType* a, int n)
{
dataType* tmp = (dataType*)malloc(sizeof(dataType) * n);
if (tmp == NULL)
{
perror("malloc:");
exit(-1);
}
//gap是一个区间的元素个数
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
//[i, i + gap - 1] [i + gap, i + 2 * gap - 1]
int begin1 = i;
int end1 = i + gap - 1;
int begin2 = i + gap;
int end2 = i + 2 * gap - 1;
int j = i;
//三种边界情况处理
//1.end2越界,此时[begin2, end2]区间不存在
if (end1 >= n)
{
end1 = n - 1;
}
//2.begin2和end2越界
//给个不存在的区间,避免重复录入数据
if (begin2 >= n)
{
begin2 = n;
end2 = n - 1;
}
//3.end2越界
if (end2 >= n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[j] = a[begin1];
++j;
++begin1;
}
else
{
tmp[j] = a[begin2];
++j;
++begin2;
}
}//end while
while (begin1 <= end1)
{
tmp[j] = a[begin1];
++j;
++begin1;
}
while (begin2 <= end2)
{
tmp[j] = a[begin2];
++j;
++begin2;
}
}//end for
//拷回原数组
for (int i = 0; i < n; ++i)
{
a[i] = tmp[i];
}
gap *= 2;
}//end while
free(tmp);
tmp = NULL;
}
// 计数排序
void CountSort(dataType* a, int n)
{
//先找到最大值和最小值确定范围
int max = a[0];
int min = a[0];
for (int i = 1; i < n; ++i)
{
if (a[i] > max)
{
max = a[i];
}
if (a[i] < min)
{
min = a[i];
}
}
int count = max - min + 1;
dataType* tmp = (dataType*)malloc(sizeof(dataType) * count);
if (tmp == NULL)
{
perror("malloc:");
exit(-1);
}
//数组全置0
memset(tmp, 0, sizeof(dataType) * count);
//保存数据个数
for (int i = 0; i < n; ++i)
{
tmp[a[i] - min]++;
}
//写入原数组
int j = 0;
for (int i = 0; i < count; ++i)
{
int k = tmp[i];
//写入重复的数据
while (k-- != 0)
{
a[j] = i + min;
++j;
}
}
free(tmp);
tmp = NULL;
}
#include"Sort.h"
void testInsertSort()
{
dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };
InsertSort(arr, sizeof(arr) / sizeof(arr[0]));
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
void testShellSort()
{
dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };
ShellSort(arr, sizeof(arr) / sizeof(arr[0]));
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
void testSelectSort()
{
dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };
SelectSort(arr, sizeof(arr) / sizeof(arr[0]));
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
void testHeapSort()
{
dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };
HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
void testBubbleSort()
{
dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };
BubbleSort(arr, sizeof(arr) / sizeof(arr[0]));
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
void testQuickSort()
{
dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };
int n = sizeof(arr) / sizeof(arr[0]);
QuickSort(arr, 0, n - 1);
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
void testQuickSortNonR()
{
dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };
int n = sizeof(arr) / sizeof(arr[0]);
QuickSortNonR(arr, 0, n - 1);
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
void testMergeSort()
{
dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };
int n = sizeof(arr) / sizeof(arr[0]);
MergeSort(arr, n);
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
void testMergeSortNonR()
{
dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };
int n = sizeof(arr) / sizeof(arr[0]);
MergeSortNonR(arr, n);
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
void testCountSort()
{
dataType arr[14] = { 5, 6, 4, 2, 8, 3, 5, 5, 8, 6, 7, 9, 1, 0 };
int n = sizeof(arr) / sizeof(arr[0]);
CountSort(arr, n);
PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
void test()
{
//testInsertSort();
//testShellSort();
//testSelectSort();
//testHeapSort();
//testBubbleSort();
//testQuickSort();
//testQuickSortNonR();
//testMergeSort();
//testMergeSortNonR();
//testCountSort();
}
//产生随机数
void getRandomNumber(dataType* array, int n)
{
for (int i = 0; i < n; ++i)
{
array[i] = rand();
}
}
//使用随机数测试性能
void testAll(int n)
{
dataType* array = (dataType*)malloc(sizeof(dataType) * n);
double begin = 0;
double end = 0;
/*getRandomNumber(array, n);
begin = GetTickCount();
InsertSort(array, n);
end = GetTickCount();
printf("直接插入排序:%.lfms\n", end - begin);*/
getRandomNumber(array, n);
begin = GetTickCount();
ShellSort(array, n);
end = GetTickCount();
printf("希尔排序:%.lfms\n", end - begin);
/*getRandomNumber(array, n);
begin = GetTickCount();
SelectSort(array, n);
end = GetTickCount();
printf("直接选择排序:%.lfms\n", end - begin);*/
getRandomNumber(array, n);
begin = GetTickCount();
HeapSort(array, n);
end = GetTickCount();
printf("堆排序:%.lfms\n", end - begin);
/*getRandomNumber(array, n);
begin = GetTickCount();
BubbleSort(array, n);
end = GetTickCount();
printf("冒泡排序:%.lfms\n", end - begin);*/
getRandomNumber(array, n);
begin = GetTickCount();
QuickSort(array, 0, n - 1);
end = GetTickCount();
printf("快速排序递归法:%.lfms\n", end - begin);
getRandomNumber(array, n);
begin = GetTickCount();
QuickSortNonR(array, 0, n - 1);
end = GetTickCount();
printf("快速排序非递归:%.lfms\n", end - begin);
getRandomNumber(array, n);
begin = GetTickCount();
MergeSort(array, n);
end = GetTickCount();
printf("归并排序递归:%.lfms\n", end - begin);
getRandomNumber(array, n);
begin = GetTickCount();
MergeSortNonR(array, n);
end = GetTickCount();
printf("归并排序非递归:%.lfms\n", end - begin);
getRandomNumber(array, n);
begin = GetTickCount();
CountSort(array, n);
end = GetTickCount();
printf("计数排序:%.lfms\n", end - begin);
}
int main()
{
//test();
srand((unsigned)time(NULL));
testAll(10000000);
system("pause");
return 0;
}10答案代码:
// 插入排序
void InsertSort(int* a, int n);
// 希尔排序
void ShellSort(int* a, int n);
void InsertSort(int* a, int n)
{
assert(a);
//最后一次,是要把n - 1这个数进行排序,则已经
//排好序的尾部为n - 2
for (int i = 0; i < n-1; ++i)
{
//end表示已经排好序的尾标
int end = i;
//首先保存要排序的数,一会就会被覆盖了
int tmp = a[end + 1];
//只要前面的数大于end + 1,则前面的这些数都向后挪动一个位置
while (end >= 0 && a[end] > tmp)
{
a[end + 1] = a[end];
--end;
}
a[end + 1] = tmp;
}
}
void TestInsertSort()
{
int a[] = { 3, 4, 6, 1, 2, 8, 3, 5, 7 };
InsertSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
void ShellSort(int* a, int n)
{
assert(a);
int gap = n;
//不能写成大于0,因为gap的值始终>=1
while (gap > 1)
{
//只有gap最后为1,才能保证最后有序
//所以这里要加1
gap = gap / 3 + 1;
//这里只是把插入排序的1换成gap即可
//但是这里不是排序完一个分组,再去
//排序另一个分组,而是整体只过一遍
//这样每次对于每组数据只排一部分
//整个循环结束之后,所有组的数据排序完成
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0 && a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
a[end + gap] = tmp;
}
}
}
void TestShellSort()
{
int a[] = { 3, 4, 6, 1, 2, 8, 3, 5, 7 };
ShellSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
// 冒泡排序
void BubbleSort(int* a, int n)
// 快速排序递归实现
// 快速排序hoare版本
int PartSort1(int* a, int left, int right);
// 快速排序挖坑法
int PartSort2(int* a, int left, int right);
// 快速排序前后指针法
int PartSort3(int* a, int left, int right);
void QuickSort(int* a, int left, int right);
// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void BubbleSort(int* a, int n)
{
assert(a);
int end = n;
while (end > 0)
{
/*
加一个标记,如果中间没有发生交换
说明前面的值都比后面的小
即本身就是有序的,最好的情况下,
它的时间复杂度就为N
*/
int flag = 0;
for (int i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
flag = 1;
}
}
if (flag == 0)
{
break;
}
--end;
}
}
void TestBubbleSort()
{
int a[] = { 3, 4, 6, 1, 2, 8, 0, 5, 7 };
BubbleSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
// 三数取中法,三个中取一个中间值
int GetMidIndex(int* a, int begin, int end)
{
int mid = begin + ((end - begin) >> 1);
if (a[begin] < a[mid])
{
if (a[mid] < a[end])
{
return mid;
}
else if (a[begin] > a[end])
{
return begin;
}
else
{
return end;
}
}
else // begin >= mid
{
if (a[mid] > a[end])
{
return mid;
}
else if (a[begin] < a[end])
{
return begin;
}
else
{
return end;
}
}
}
int PartSort1(int* a, int begin, int end)
{
int midindex = GetMidIndex(a, begin, end);
Swap(&a[begin], &a[midindex]);
int key = a[begin];
int start = begin;
/*
这里要从右边走,如果从左边走,
可能最后一步,如果找不到大于
基准值的,会导致begin == end
即相遇,但是右边还没有走,所以
这里的值一定大于基准值,最后交换
就会出问题,所以一定要从右边走,
即使最后一次找不到小于基准值的,
会和左边相遇,而左边此时还没走,
一定比基准值小,最后交换肯定没有问题
*/
while (begin < end)
{
// end 找小
while (begin < end && a[end] >= key)
--end;
// begin找大
while (begin < end && a[begin] <= key)
++begin;
Swap(&a[begin], &a[end]);
}
//最后的交换一定要保证a[begin] < a[start], 所以要从右边走
Swap(&a[begin], &a[start]);
return begin;
}
int PartSort2(int* a, int begin, int end)
{
//begin是坑
int key = a[begin];
while (begin < end)
{
while (begin < end && a[end] >= key)
--end;
// end给begin这个坑,end就变成了新的坑。
a[begin] = a[end];
while (begin < end && a[begin] <= key)
++begin;
// end给begin这个坑,begin就变成了新的坑。
a[end] = a[begin];
}
a[begin] = key;
return begin;
}
/*
前后指针法
*/
int PartSort3(int* a, int begin, int end)
{
int midindex = GetMidIndex(a, begin, end);
Swap(&a[begin], &a[midindex]);
int key = a[begin];
int prev = begin;
int cur = begin + 1;
while (cur <= end)
{
// cur找小,把小的往前翻,大的往后翻
if (a[cur] < key && ++prev != cur)
Swap(&a[cur], &a[prev]);
++cur;
}
Swap(&a[begin], &a[prev]);
return prev;
}
// []
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
if (right - left + 1 < 10)
{
InsertSort(a+left, right - left + 1);
}
else
{
int div = PartSort3(a, left, right);
//[left, div-1]
//[div+1, right]
QuickSort(a, left, div - 1);
QuickSort(a, div + 1, right);
}
}
//用栈模拟递归,用队列也可以实现
void QuickSortR(int* a, int left, int right)
{
Stack st;
StackInit(&st, 10);
//先入大区间
if (left < right)
{
StackPush(&st, right);
StackPush(&st, left);
}
//栈不为空,说明还有没处理的区间
while (StackEmpty(&st) != 0)
{
left = StackTop(&st);
StackPop(&st);
right = StackTop(&st);
StackPop(&st);
//快排单趟排序
int div = PartSort1(a, left, right);
// [left div-1]
// 把大于1个数的区间继续入栈
if (left < div - 1)
{
StackPush(&st, div - 1);
StackPush(&st, left);
}
// [div+1, right]
if (div+1 < right)
{
StackPush(&st, right);
StackPush(&st, div + 1);
}
}
}
void TestQuickSort()
{
int a[] = { 3, 4, 6, 1, 2, 8, 0, 5, 7 };
QuickSortR(a, 0, sizeof(a) / sizeof(int)-1);
PrintArray(a, sizeof(a) / sizeof(int));
}
// 归并排序递归实现
void MergeSort(int* a, int n)
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
// 计数排序
void CountSort(int* a, int n)
void _MergeSort(int* a, int left, int right, int* tmp)
{
if (left >= right)
return;
int mid = left + ((right - left) >> 1);
// [left, mid]
// [mid+1, right]
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid+1, right, tmp);
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
tmp[index++] = a[begin1++];
else
tmp[index++] = a[begin2++];
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
memcpy(a+left, tmp+left, sizeof(int)*(right - left+1));
}
void MergeSort(int* a, int n)
{
assert(a);
int* tmp = (int*)malloc(sizeof(int)*n);
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}
/*
非递归排序与递归排序相反,将一个元素与相邻元素构成有序数组,
再与旁边数组构成有序数组,直至整个数组有序。
要有mid指针传入,因为不足一组数据时,重新计算mid划分会有问题
需要指定mid的位置
*/
void merge(int* a, int left, int mid, int right, int* tmp)
{
// [left, mid]
// [mid+1, right]
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
tmp[index++] = a[begin1++];
else
tmp[index++] = a[begin2++];
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
memcpy(a+left, tmp+left, sizeof(int)*(right - left+1));
}
/*
k用来表示每次k个元素归并
*/
void mergePass(int *arr, int k, int n, int *temp)
{
int i = 0;
//从前往后,将2个长度为k的子序列合并为1个
while(i < n - 2*k + 1)
{
merge(arr, i, i + k - 1, i + 2*k - 1, temp);
i += 2*k;
}
//合并区间[i, n - 1]有序的左半部分[i, i + k - 1]以及不及一个步长的右半部分[i + k, n - 1]
if(i < n - k )
{
merge(arr, i, i + k - 1,n-1, temp);
}
}
// 归并排序非递归版
void MergeSortNonR(int *arr,int length)
{
int k = 1;
int *temp = (int *)malloc(sizeof(int) * length);
while(k < length)
{
mergePass(arr, k, length, temp);
k *= 2;
}
free(temp);
}
void TestMergeSort()
{
int a[] = { 3, 4, 6, 1, 2, 8, 0, 5, 7 };
MergeSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
// O(Max(N, 范围))
// O(N+范围) 时间复杂度
// O(范围) 空间复杂度
void CountSort(int* a, int n)
{
int max = a[0], min = a[0];
for (int i = 0; i < n; ++i)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
//找到数据的范围
int range = max - min + 1;
int* countArray = (int*)malloc(range*sizeof(int));
memset(countArray, 0, sizeof(int)*range);
//存放在相对位置,可以节省空间
for (int i = 0; i < n; ++i)
{
countArray[a[i] - min]++;
}
//可能存在重复的数据,有几个存几个
int index = 0;
for (int i = 0; i < range; ++i)
{
while (countArray[i]--)
{
a[index++] = i+min;
}
}
}
void TestCountSort()
{
int a[] = { 3, 4, 6, 2, 8, 5, 2, 2, 9, 9, 1000000, 99999};
CountSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
void TestSortOP()
{
const int n = 1000000;
int* a1 = (int*)malloc(sizeof(int)*n);
int* a2 = (int*)malloc(sizeof(int)*n);
int* a3 = (int*)malloc(sizeof(int)*n);
int* a4 = (int*)malloc(sizeof(int)*n);
int* a5 = (int*)malloc(sizeof(int)*n);
int* a6 = (int*)malloc(sizeof(int)*n);
int* a7 = (int*)malloc(sizeof(int)*n);
int* a8 = (int*)malloc(sizeof(int)*n);
srand(time(0));
for (int i = 0; i < n; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
a8[i] = a1[i];
}
a8[n] = 100000000;
size_t begin1 = clock();
//InsertSort(a1, n);
size_t end1 = clock();
printf("%u\n", end1 - begin1);
size_t begin2 = clock();
ShellSort(a2, n);
size_t end2 = clock();
printf("%u\n", end2 - begin2);
size_t begin3 = clock();
//SelectSort(a3, n);
size_t end3 = clock();
printf("%u\n", end3 - begin3);
size_t begin4 = clock();
HeapSort(a4, n);
size_t end4 = clock();
printf("%u\n", end4 - begin4);
size_t begin5 = clock();
//BubbleSort(a5, n);
size_t end5 = clock();
printf("%u\n", end5 - begin5);
size_t begin6 = clock();
QuickSort(a6, 0, n-1);
size_t end6 = clock();
printf("%u\n", end6 - begin6);
size_t begin7 = clock();
MergeSort(a7, n);
size_t end7 = clock();
printf("%u\n", end7 - begin7);
size_t begin8 = clock();
CountSort(a8, n);
size_t end8 = clock();
printf("%u\n", end8 - begin8);
}
11.题目:
912. 排序数组
答案








![[架构之路-179]-《软考-系统分析师》-19- 系统可靠性分析与设计 - 故障模型、可靠性模型、可靠性分析](https://img-blog.csdnimg.cn/f38135dbfcce4e41b4ed8df5eb33851f.png)