八大排序算法
文章目录
- 八大排序算法
- 一、插入排序
- 1.代码实现
- 2.思路+图解
- 二、希尔排序
- 1.代码实现
- 2.思路+图解
- 三、选择排序(优化版)
- 1.代码实现
- 2.思路+图解
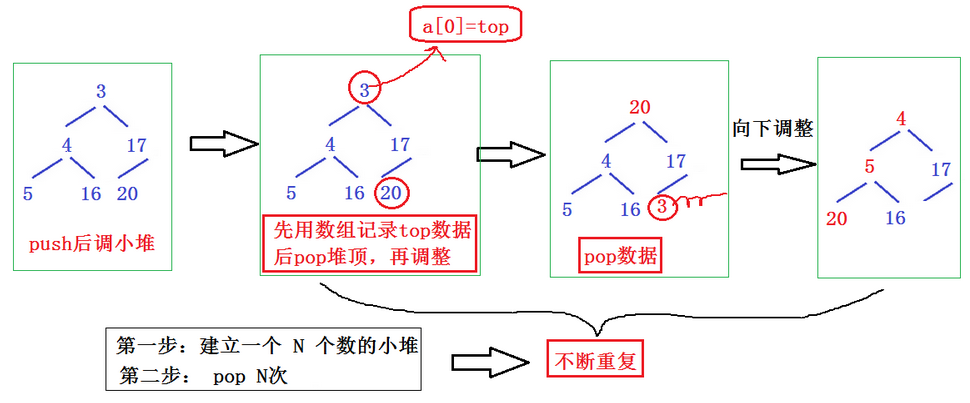
- 四、堆排序
- 1.代码实现
- 2.思路+图解
- 五、冒泡排序
- 1.代码实现
- 2.思路+图解
- 六、快速排序
- 1.递归版本
- 2.非递归版本
- 3.快速排序的两个优化
- 七、归并排序
- 1.递归版本(图解+源码)
- 2.非递归版本(图解+源码)
- 3.数组越界问题以及优化
- 八、计数排序
- 1.代码实现
- 2.思路+图解
- 九、八大排序对比
- 总结
一、插入排序

1.代码实现
代码如下(示例):
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; ++i)
{
// [0,end]有序,把end+1位置的值插入,保持有序
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
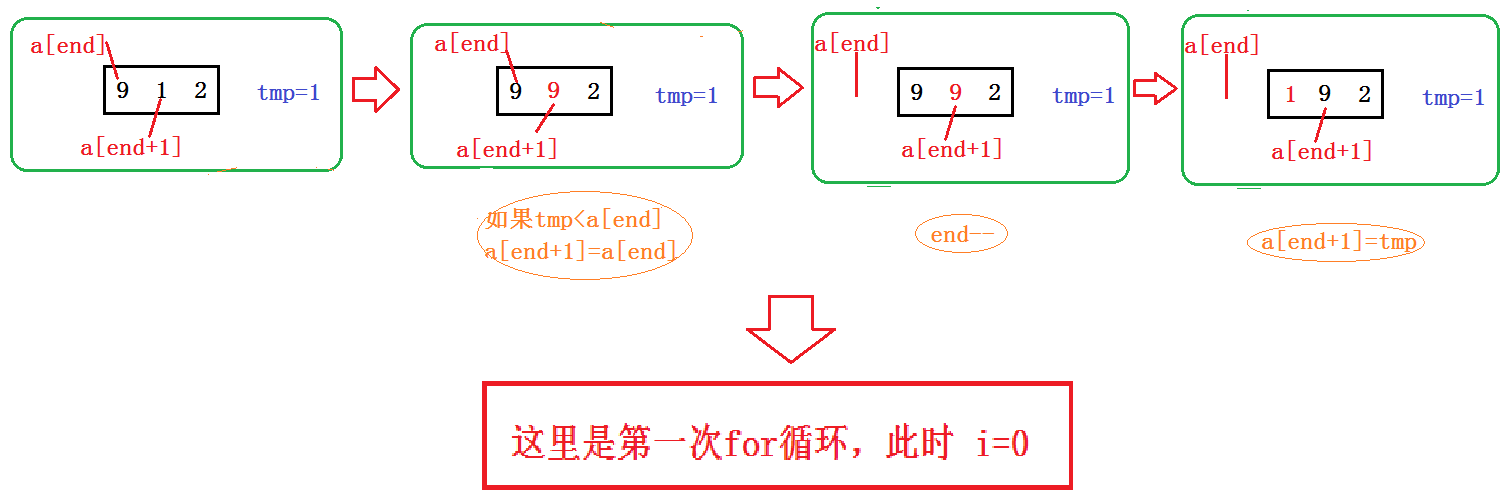
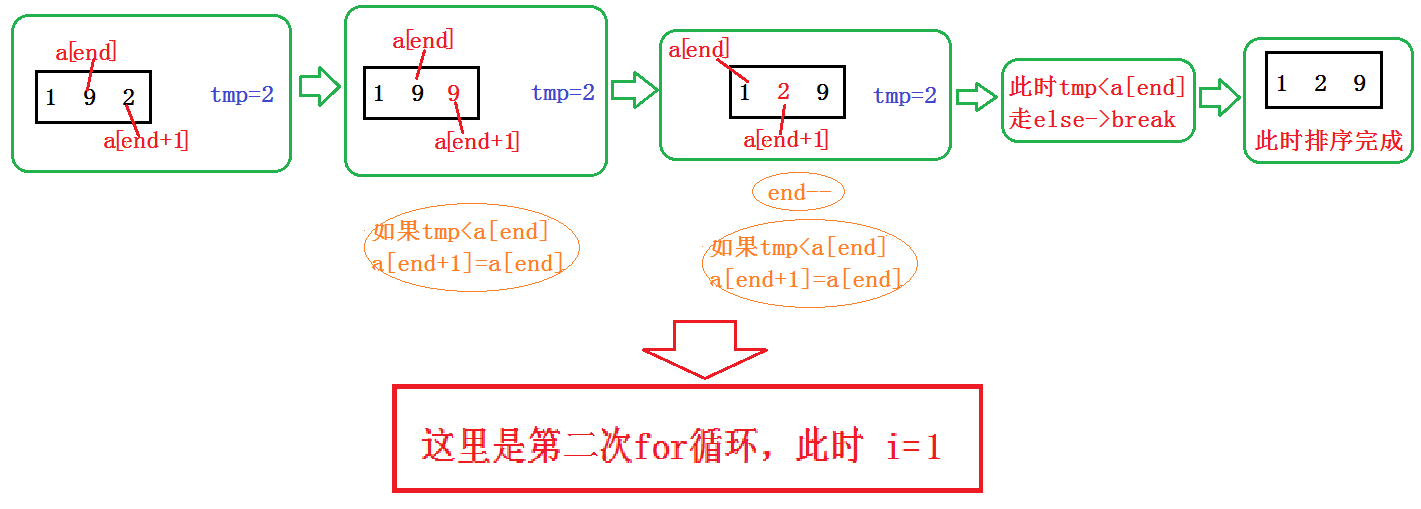
2.思路+图解
为了方便画图解,我们直接来排序 9 1 2 这三个数!


二、希尔排序
1.代码实现
代码如下(示例):
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
//gap = gap / 2;
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
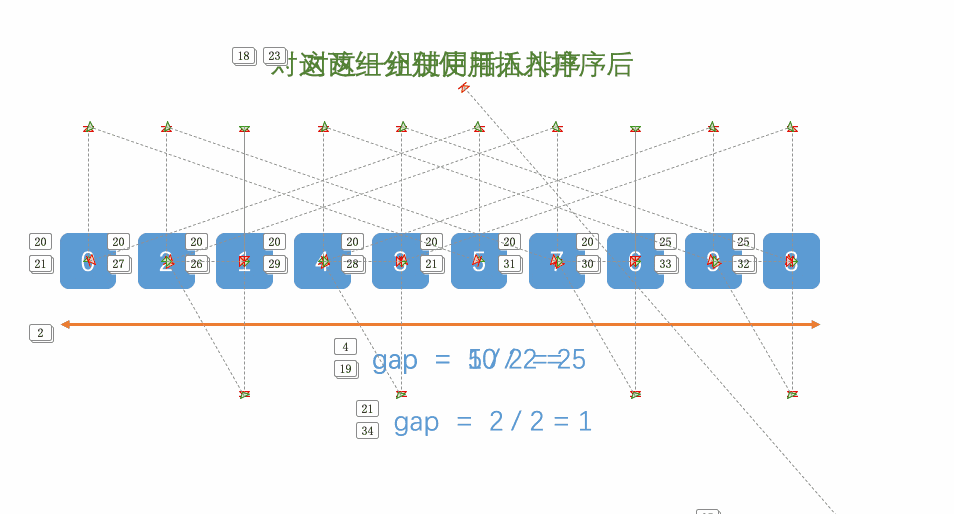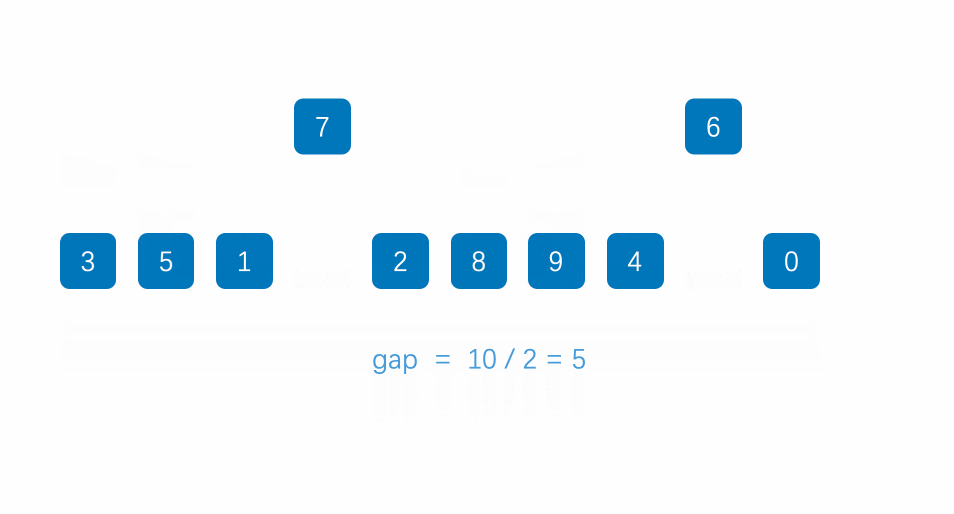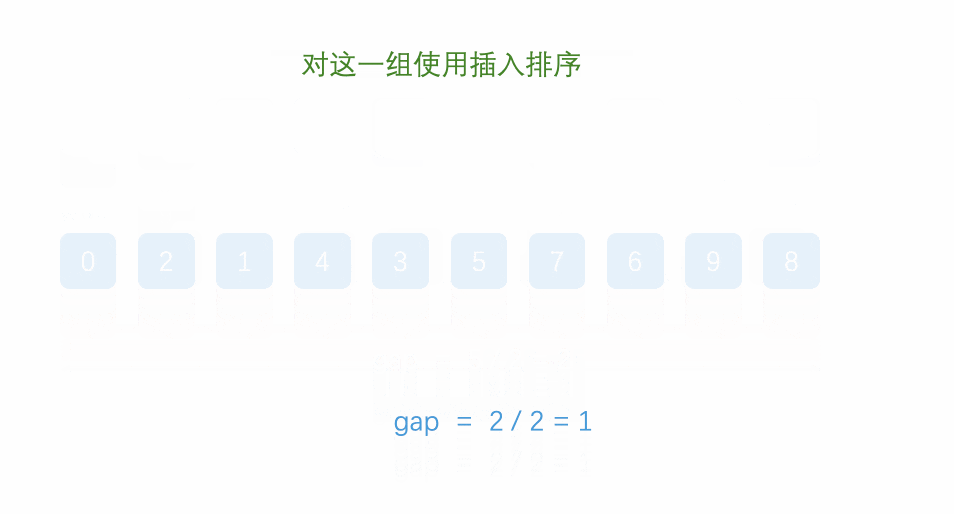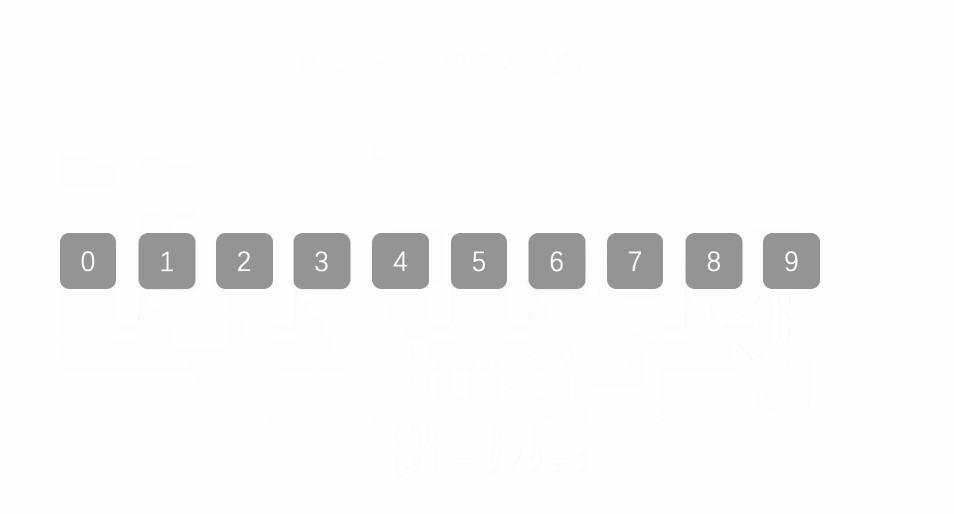
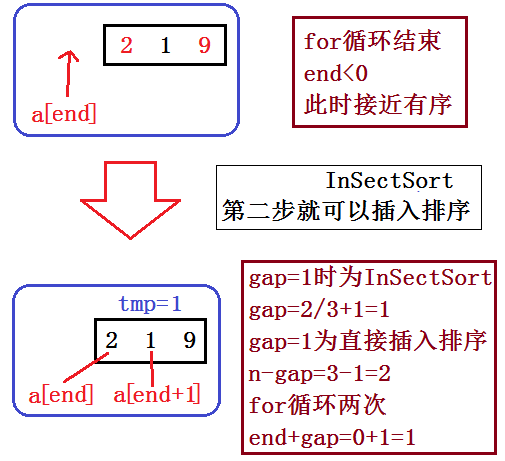
2.思路+图解

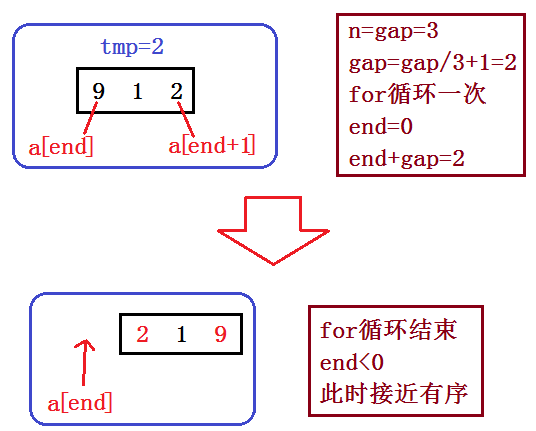
以上为希尔排序的第一步:预排序,以下为希尔排序的第二步:直接插入排序
三、选择排序(优化版)
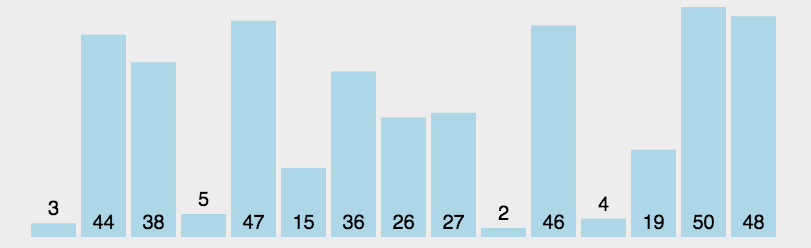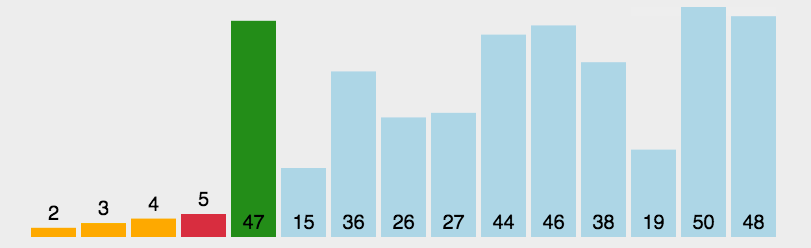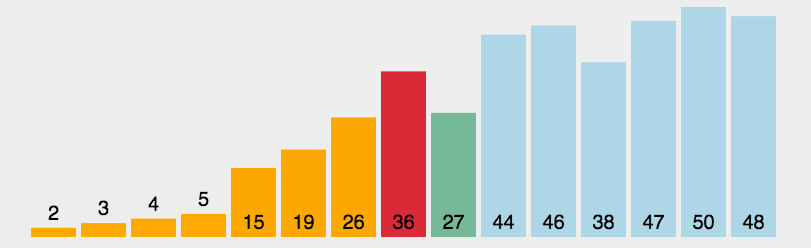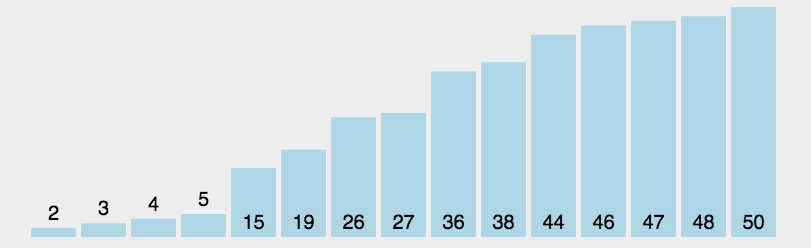
1.代码实现
代码如下(示例):
void SelectSort(int* a, int n)
{
assert(a);
int begin = 0, end = n - 1;
while (begin < end)
{
int mini = begin, maxi = begin;
for (int i = begin + 1; i <= end; ++i)
{
if (a[i] < a[mini])
mini = i;
if (a[i] > a[maxi])
maxi = i;
}
Swap(&a[begin], &a[mini]);
// 如果begin和maxi重叠,那么要修正一下maxi的位置
if (begin == maxi)
{
maxi = mini;
}
Swap(&a[end], &a[maxi]);
++begin;
--end;
}
}
2.思路+图解
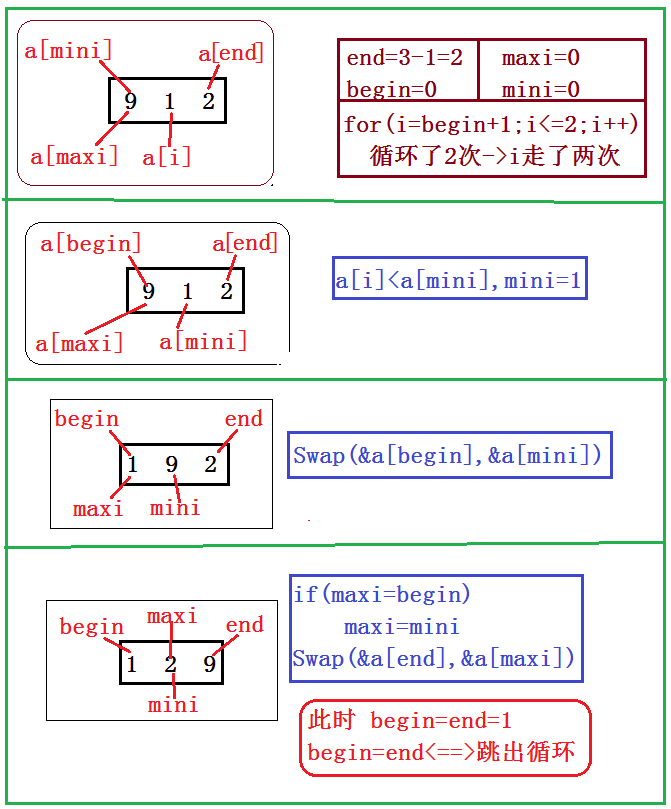
四、堆排序
堆排序详细讲解在这里!!!
1.代码实现
代码如下(示例):
void AdjustDwon(int* a, int size, int parent)
{
int child = parent * 2 + 1;
while (child < size)
{
// 选出左右孩子中小/大的那个
if (child + 1 < size && a[child + 1] > a[child])
{
++child;
}
// 孩子跟父亲比较
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
// 降序 -- 建小堆
// 升序 -- 建大堆
void HeapSort(int* a, int n)
{
// 建堆方式2:O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDwon(a, n, i);
}
// O(N*logN)
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDwon(a, end, 0);
--end;
}
}
2.思路+图解
五、冒泡排序
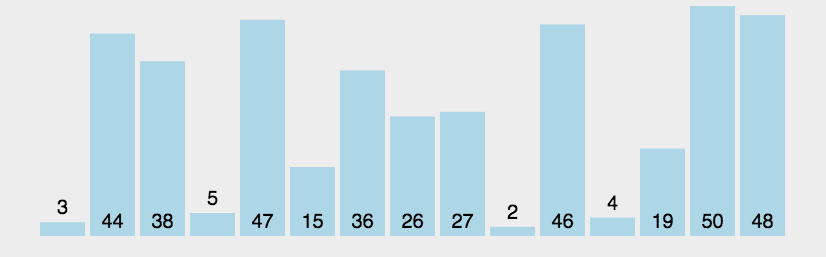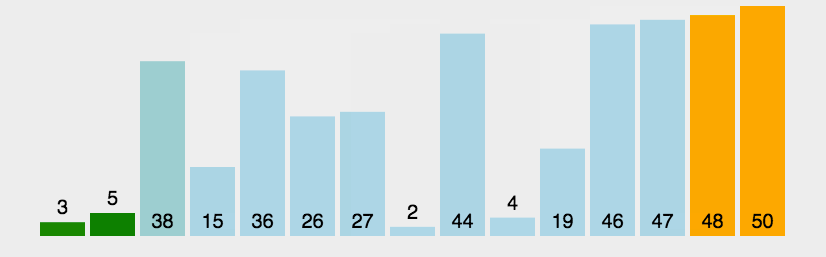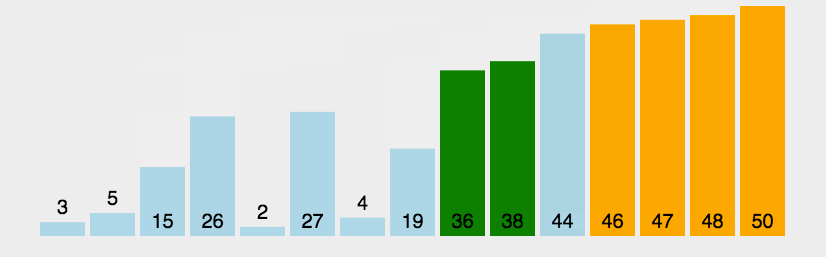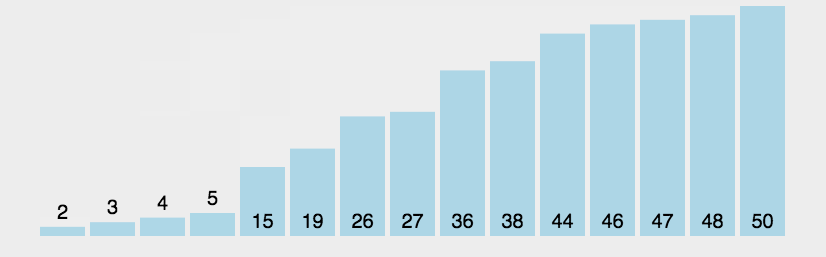
1.代码实现
代码如下(示例):
void BubbleSort(int* a, int n)
{
assert(a);
for (int j = 0; j < n - 1; ++j)
{
int exchange = 0;
for (int i = 1; i < n - j; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
{
break;
}
}
}
2.思路+图解

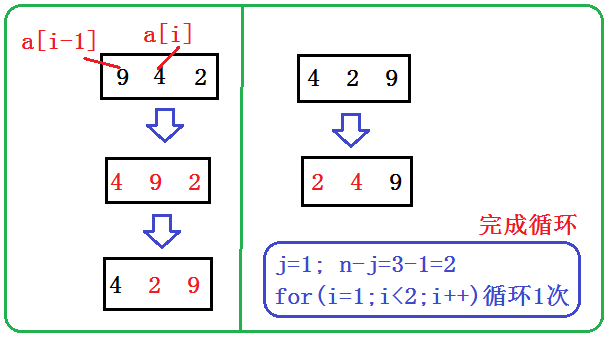
六、快速排序
1.递归版本
(1)Hoare版本

代码如下(示例):
// Hoare
int PartSort1(int* a, int begin, int end)
{
int left = begin, right = end;
int keyi = left;
while (left < right)
{
// 右边先走,找小
while (left < right && a[right] >= a[keyi])
{
--right;
}
// 左边再走,找大
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);
keyi = left;
return keyi;
}

(2)挖坑法

代码如下(示例):
// 挖坑法
int PartSort2(int* a, int begin, int end)
{
int key = a[begin];
int piti = begin;
while (begin < end)
{
// 右边找小,填到左边的坑里面去。这个位置形成新的坑
while (begin < end && a[end] >= key)
{
--end;
}
a[piti] = a[end];
piti = end;
// 左边找大,填到右边的坑里面去。这个位置形成新的坑
while (begin < end && a[begin] <= key)
{
++begin;
}
a[piti] = a[begin];
piti = begin;
}
a[piti] = key;
return piti;
}
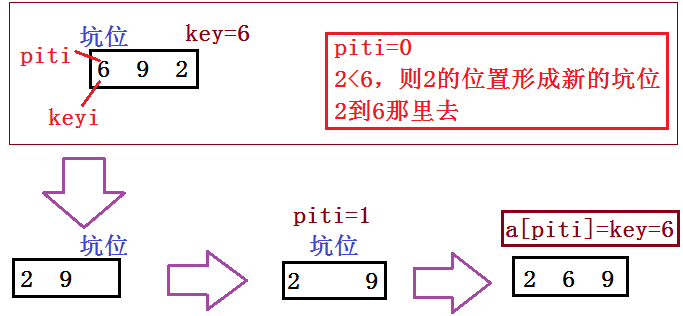
(3)前后指针法

代码如下(示例):
//快速排序(前后指针法)
void QuickSort3(int* a, int begin, int end)
{
if (begin >= end)//当只有一个数据或是序列不存在时,不需要进行操作
return;
//三数取中
int midIndex = GetMidIndex(a, begin, end);
Swap(&a[begin], &a[midIndex]);
int prev = begin;
int cur = begin + 1;
int keyi = begin;
while (cur <= end)//当cur未越界时继续
{
if (a[cur] < a[keyi] && ++prev != cur)//cur指向的内容小于key
{
Swap(&a[prev], &a[cur]);
}
cur++;
}
int meeti = prev;//cur越界时,prev的位置
Swap(&a[keyi], &a[meeti]);//交换key和prev指针指向的内容
QuickSort3(a, begin, meeti - 1);//key的左序列进行此操作
QuickSort3(a, meeti + 1, end);//key的右序列进行此操作
}
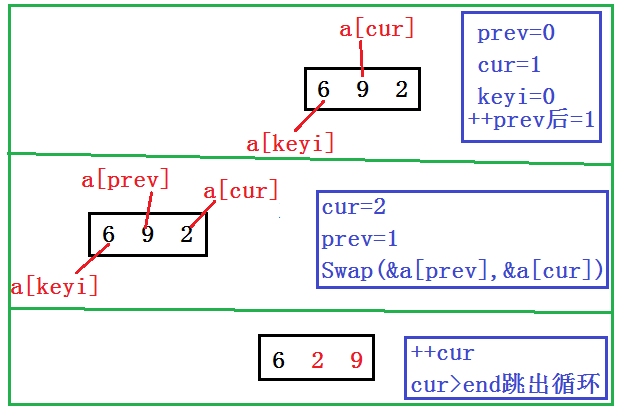
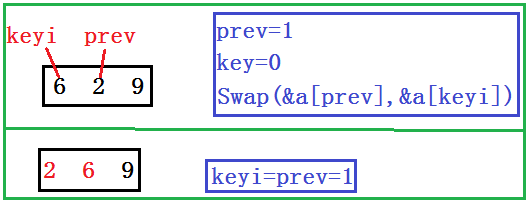
2.非递归版本


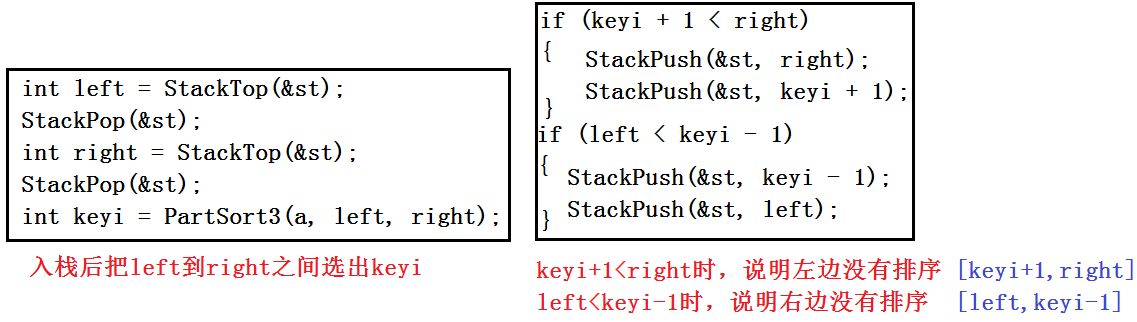
代码如下(示例):
//快速排序(非递归实现)
void QuickSortNonR(int* a, int begin, int end)
{
Stack st;//创建栈
StackInit(&st);//初始化栈
StackPush(&st, begin);//待排序列的L
StackPush(&st, end);//待排序列的R
while (!StackEmpty(&st))
{
int right = StackTop(&st);//读取R
StackPop(&st);//出栈
int left = StackTop(&st);//读取L
StackPop(&st);//出栈
//该处调用的是Hoare版本的单趟排序
int keyi = PartSort1(a, left, right);
if (left < keyi - 1)//该序列的左序列还需要排序
{
StackPush(&st, left);//左序列的L入栈
StackPush(&st, keyi - 1);//左序列的R入栈
}
if (keyi + 1 < right)// 该序列的右序列还需要排序
{
StackPush(&st, keyi + 1);//右序列的L入栈
StackPush(&st, right);//右序列的R入栈
}
}
StackDestroy(&st);//销毁栈
}
3.快速排序的两个优化
优化一:三数取中
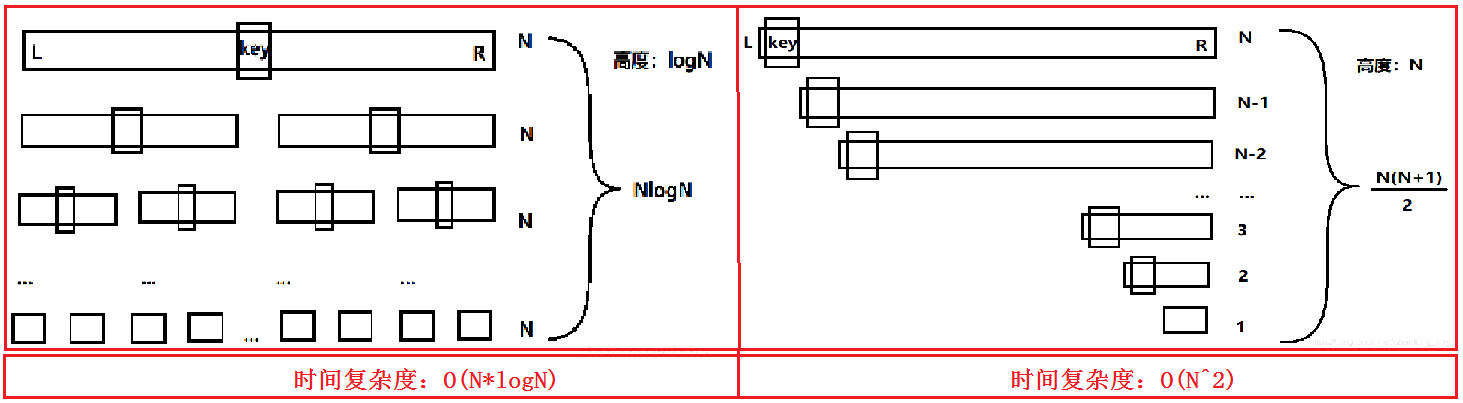

三数取中的核心就是:用 if 和 else语句对数进行判断!!!
代码如下(示例):
int GetMidIndex(int* a, int begin, int end)
{
int mid = (begin + end) / 2;
if (a[begin] < a[mid])
{
if (a[mid] < a[end])
{
return mid;
}
else if (a[begin] < a[end])
{
return end;
}
else
{
return begin;
}
}
else // (a[begin] >= a[mid])
{
if (a[mid] > a[end])
{
return mid;
}
else if (a[begin] < a[end])
{
return begin;
}
else
{
return end;
}
}
}
优化二:小区间优化减少递归次数
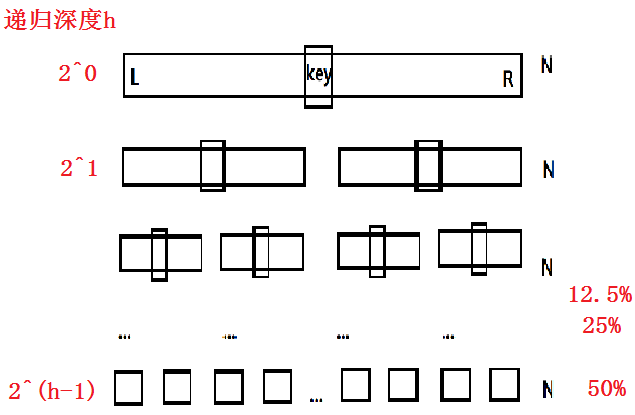

代码如下(示例):
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
if (end - begin > 10)
{
int keyi = PartSort2(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
else
{
InsertSort(a + begin, end - begin + 1);
}
}
七、归并排序

1.递归版本(图解+源码)
代码如下(示例):
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin >= end)
return;
int mid = (begin + end) / 2;
// [begin, mid] [mid+1, end] 分治递归,让子区间有序
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
//归并 [begin, mid] [mid+1, end]
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
// 把归并数据拷贝回原数组
memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}

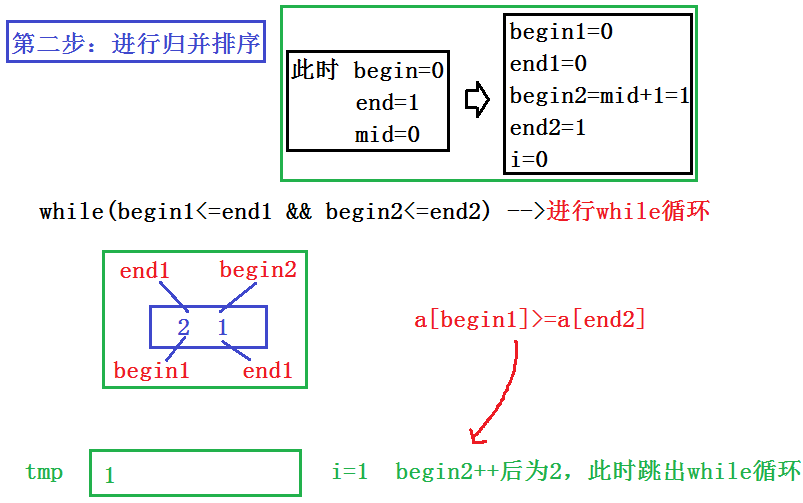


2.非递归版本(图解+源码)
代码如下(示例):
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
// 休息11:48继续
int gap = 1;
while (gap < n)
{
//printf("gap=%d->", gap);
for (int i = 0; i < n; i += 2 * gap)
{
// [i,i+gap-1][i+gap, i+2*gap-1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
// end1越界或者begin2越界,则可以不归并了
if (end1 >= n || begin2 >= n)
{
break;
}
else if (end2 >= n)
{
end2 = n - 1;
}
//printf("[%d,%d] [%d, %d]--", begin1, end1, begin2, end2);
int m = end2 - begin1 + 1;
int j = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * m);
}
gap *= 2;
}
free(tmp);
}





3.数组越界问题以及优化
当归并排序的数组个数是奇数个时,会出现数组越界问题,以致于程序崩溃


代码如下(示例):
// 越界-修正边界
if (end1 >= n)
{
end1 = n - 1;
// [begin2, end2]修正为不存在区间
begin2 = n;
end2 = n - 1;
}
else if (begin2 >= n)
{
// [begin2, end2]修正为不存在区间
begin2 = n;
end2 = n - 1;
}
else if(end2 >= n)
{
end2 = n - 1;
}
八、计数排序
1.代码实现
代码如下(示例):
// 时间复杂度:O(max(range, N))
// 空间复杂度:O(range)
void CountSort(int* a, int n)
{
int min = a[0], max = a[0];
for (int i = 1; i < n; ++i)
{
if (a[i] < min)
min = a[i];
if (a[i] > max)
max = a[i];
}
// 统计次数的数组
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
if (count == NULL)
{
printf("malloc fail\n");
exit(-1);
}
memset(count, 0, sizeof(int) * range);
// 统计次数
for (int i = 0; i < n; ++i)
{
count[a[i] - min]++;
}
// 回写-排序
int j = 0;
for (int i = 0; i < range; ++i)
{
// 出现几次就会回写几个i+min
while (count[i]--)
{
a[j++] = i + min;
}
}
}
2.思路+图解




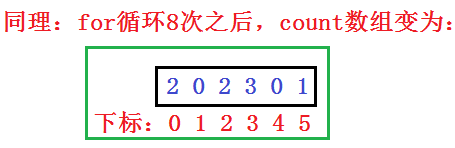


九、八大排序对比
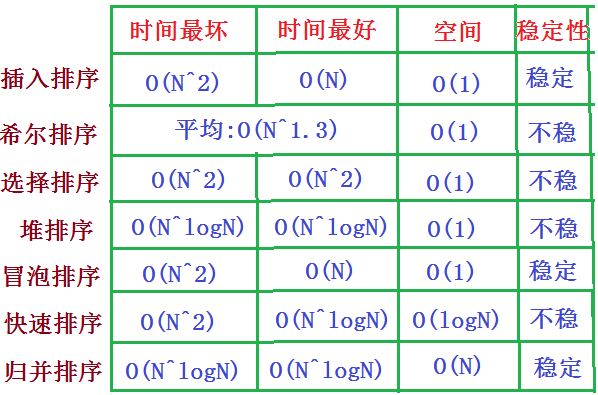
总结
以上就是今天要讲的内容,本文介绍了校招中重点的八大排序,到这里初阶数据结构就结束了,接下来带来c++和Linux的内容,感谢大家的点赞支持!