这是一道 中等难度 的题

题目来自： https://leetcode.cn/problems/subsets/

题目

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3] 
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]] 

示例 2：

输入：nums = [0] 
输出：[[],[0]] 

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10
• nums 中的所有元素 互不相同

题解

因为每个数字都有 不选 和 选 两种方案，所以最终会有 $2^n$ 个答案，n为数组长度。

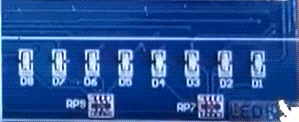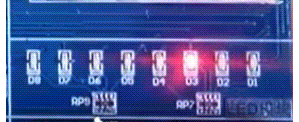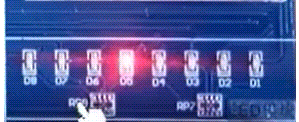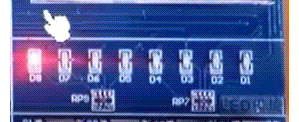
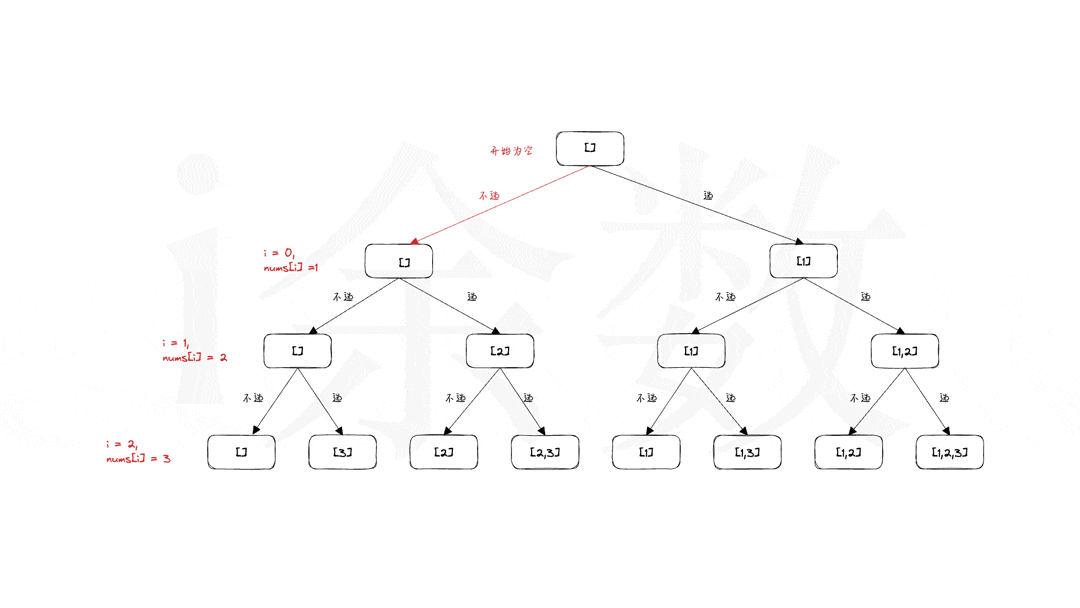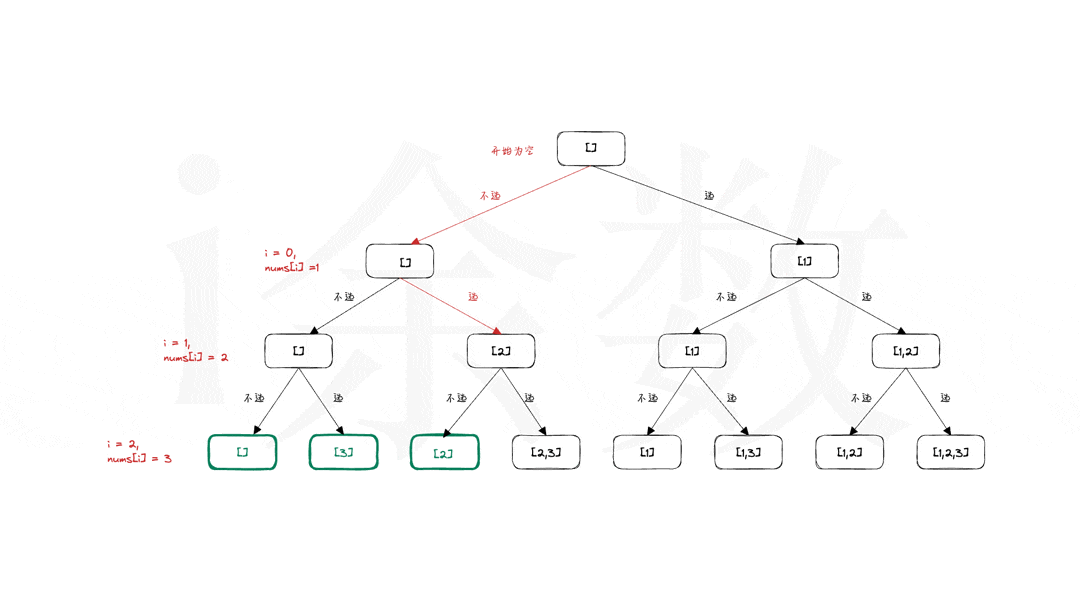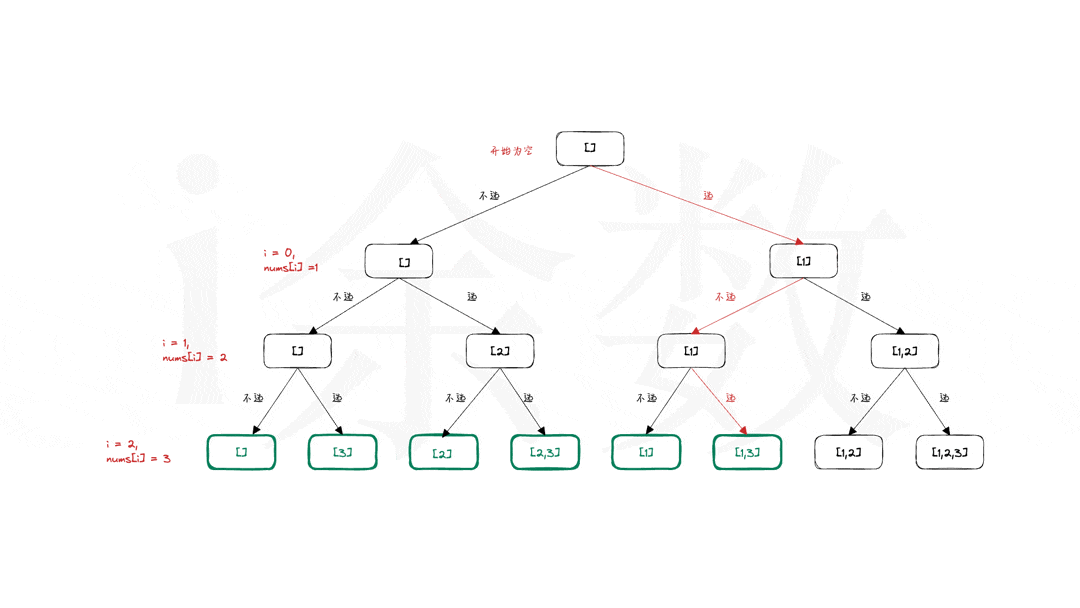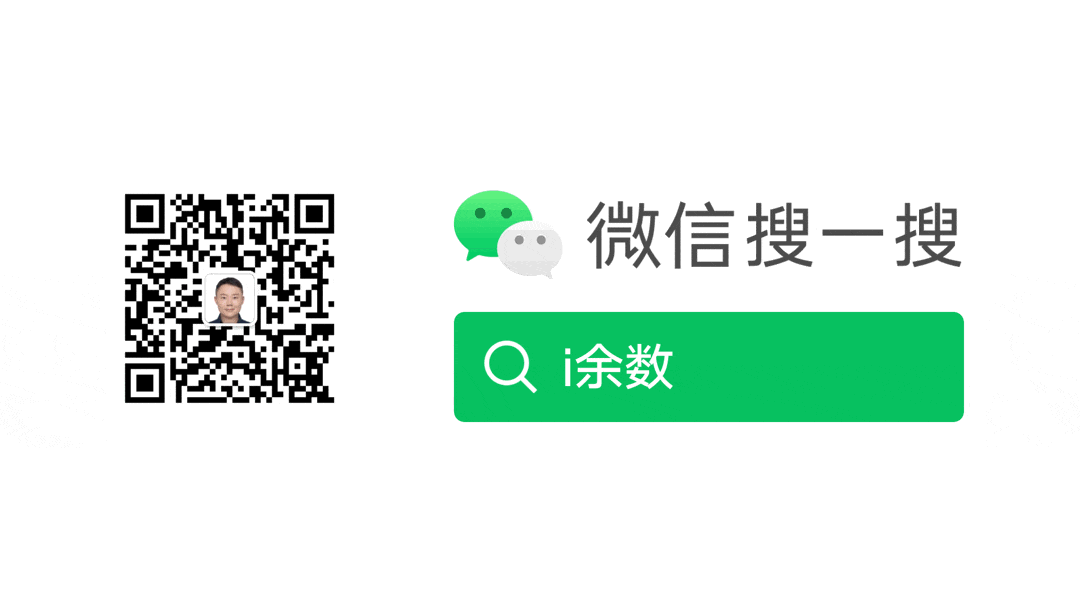
以 nums = [1,2,3] 为例子，共有 $2^3=8$ 个答案。如下图所示：

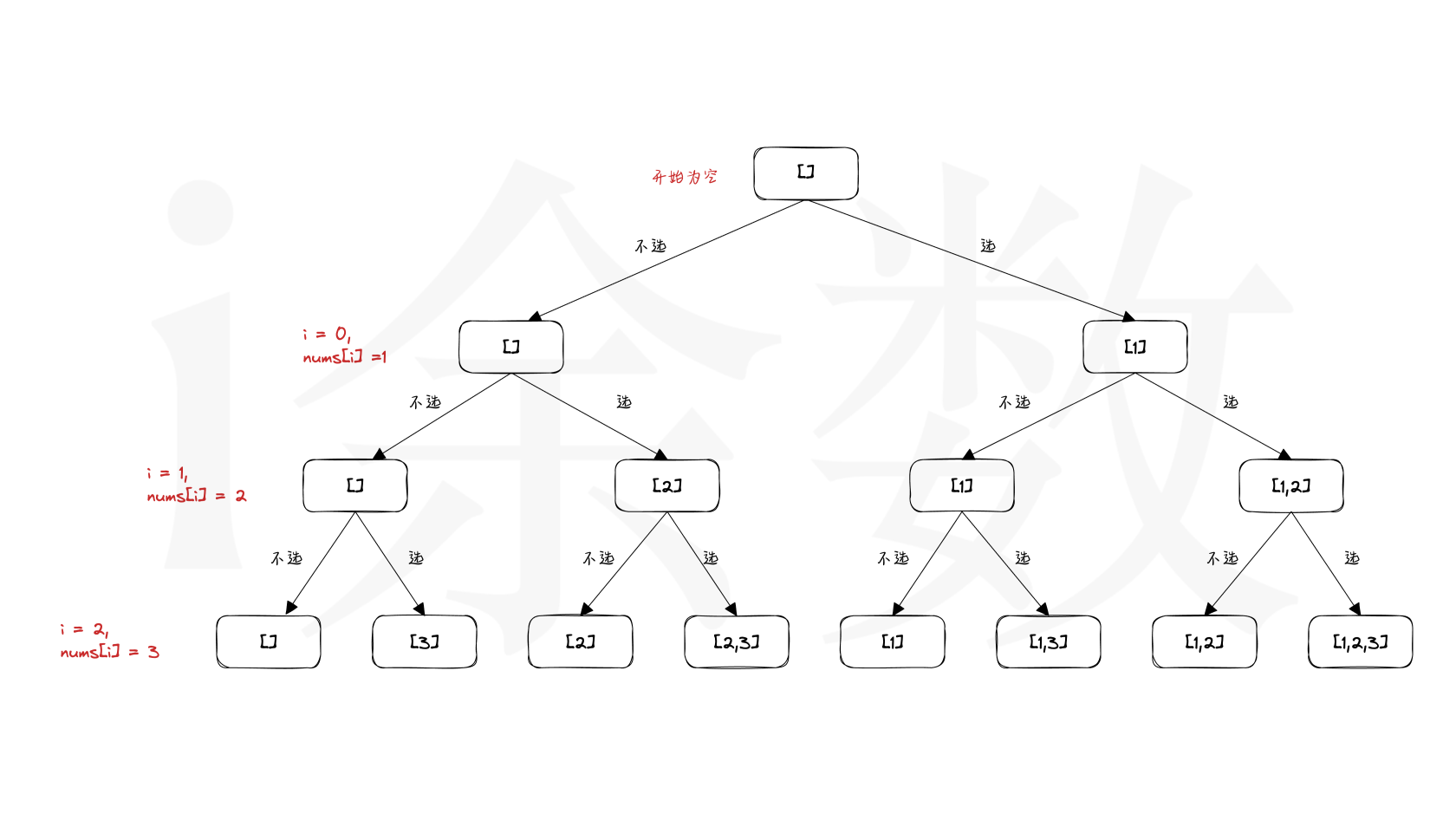
这种树形结构的题，一般都可以使用递归的解法，那么就需要确定递归三要素：

1. 递归函数 recursion: 每次都有选和不选两个操作，并继续往下递归。
2. 边界条件：i == n, 数组nums中的n个数都已经计算完成，记录答案并返回。
3. 还原现场：如动图展示中，箭头由红色回退到黑色的时候，子集subSet中的数字也是要同时回退的。

Java 代码实现

class Solution {
    private int n;
    private List<Integer> subSet = new ArrayList<>();
    private List<List<Integer>> ans = new ArrayList<>();
    public List<List<Integer>> subsets(int[] nums) {
        n = nums.length;
        recursion(0, nums);
        return ans;

    }

    private void recursion(int i, int[] nums){

        if(i == n){
            ans.add(new ArrayList(subSet));
            return;
        }

        // 不选
        recursion(i + 1, nums);

        // 选
        subSet.add(nums[i]);
        recursion(i + 1, nums);
        subSet.remove(subSet.size() - 1);
    }
}

Go代码实现

var ans [][]int
var subSet []int

func subsets(nums []int) [][]int {
    subSet = []int{}
    ans = [][]int{}

    recursion(0, nums)

    return ans
}

func recursion(i int, nums []int) {
    if i == len(nums) {
        temp := make([]int, len(subSet))
        copy(temp, subSet)
        ans = append(ans, temp)
        return
    }

    // 不选
    recursion(i + 1, nums)

    // 选
    subSet = append(subSet, nums[i])
    recursion(i + 1, nums)
    subSet = subSet[:len(subSet) - 1]
}