逻辑回归的损失函数 以及 梯度下降
- 逻辑回归的损失函数
- 逻辑回归的 Loss
- 逻辑回归的 Cost
- 逻辑回归的梯度下降
- 总公式
- 推导公式
- 梯度下降动画效果展示
- Reference
逻辑回归的损失函数
逻辑回归的 Loss
逻辑回归是一种用于二分类问题的监督学习算法,其损失函数采用交叉熵(Cross-Entropy)损失函数。
公式如下:
l
o
s
s
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
,
y
(
i
)
)
=
{
−
log
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
if
y
(
i
)
=
1
−
log
(
1
−
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
if
y
(
i
)
=
0
\begin{equation} loss(f_{\mathbf{\vec{w}},b}(\vec{x}^{(i)}), y^{(i)}) = \begin{cases} - \log\left(f_{\vec{w},b}\left( \vec{x}^{(i)} \right) \right) & \text{if $y^{(i)}=1$}\\ - \log \left( 1 - f_{\vec{w},b}\left( \vec{x}^{(i)} \right) \right) & \text{if $y^{(i)}=0$} \end{cases} \end{equation}
loss(fw,b(x(i)),y(i))={−log(fw,b(x(i)))−log(1−fw,b(x(i)))if y(i)=1if y(i)=0
简化为:
l
o
s
s
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
,
y
(
i
)
)
=
y
(
i
)
∗
(
−
l
o
g
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
)
+
(
1
−
y
(
i
)
)
∗
(
−
l
o
g
(
1
−
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
)
loss(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)})=y^{(i)}*(-log(f_{\vec{w},b}(\vec{x}^{(i)})))+(1-y^{(i)})*(-log(1-f_{\vec{w},b}(\vec{x}^{(i)})))
loss(fw,b(x(i)),y(i))=y(i)∗(−log(fw,b(x(i))))+(1−y(i))∗(−log(1−fw,b(x(i))))
函数图像如下:

Q:为什么逻辑回归函数不使用平方误差损失函数?
A: 由于平方误差损失函数会对预测值和真实值之间的误差进行平方,所以对于偏离目标值较大的预测值具有较大的惩罚,使用平方误差损失函数可能导致训练出来的模型过于敏感,对于偏离目标值较远的预测值可能会出现较大的误差,从而导致出现 “震荡”现象:
震荡现象: 平方误差损失函数的梯度在误差较小时非常小,而在误差较大时则非常大,这导致在误差较小时,模型参数的微小变化可能会导致损失函数的微小变化,而在误差较大时,模型参数的变化则会导致损失函数的大幅变化,从而产生了振荡现象。

震荡现象对于梯度下降来说是致命的,因为振荡现象意味着有着众多“局部最优”;而局部最优明显不是我们想要的解,因为我们希望能够最终抵达“全局最优”。
逻辑回归的 Cost
公式:
J
(
w
⃗
,
b
)
=
1
m
∑
i
=
0
m
−
1
[
l
o
s
s
(
f
w
⃗
,
b
(
x
(
i
)
)
,
y
(
i
)
)
]
J(\vec{w},b)=\frac 1 m \sum ^{m-1} _{i=0} [loss(f_{\vec{w},b}(x^{(i)}),y^{(i)})]
J(w,b)=m1i=0∑m−1[loss(fw,b(x(i)),y(i))]
代码:
def compute_cost_logistic(X, y, w, b):
m = X.shape[0]
cost = 0.0
for i in range(m):
z_i = np.dot(X[i],w) + b
f_wb_i = sigmoid(z_i)
cost += -y[i]*np.log(f_wb_i) - (1-y[i])*np.log(1-f_wb_i)
cost = cost / m
return cost
def sigmoid(z):
f_wb = 1/(1 + np.exp(-z))
return f_wb
逻辑回归的梯度下降
总公式
公式:
repeat until convergence:
{
w
j
=
w
j
−
α
∂
J
(
w
⃗
,
b
)
∂
w
j
for j := 0..n-1
b
=
b
−
α
∂
J
(
w
⃗
,
b
)
∂
b
}
\begin{align*} &\text{repeat until convergence:} \; \lbrace \\ & \; \; \;w_j = w_j - \alpha \frac{\partial J(\vec{w},b)}{\partial w_j} \; & \text{for j := 0..n-1} \\ & \; \; \; \; \;b = b - \alpha \frac{\partial J(\vec{w},b)}{\partial b} \\ &\rbrace \end{align*}
repeat until convergence:{wj=wj−α∂wj∂J(w,b)b=b−α∂b∂J(w,b)}for j := 0..n-1
其中:
∂
J
(
w
⃗
,
b
)
∂
w
j
=
1
m
∑
i
=
0
m
−
1
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
∂
J
(
w
⃗
,
b
)
∂
b
=
1
m
∑
i
=
0
m
−
1
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
−
y
(
i
)
)
\frac {\partial J(\vec{w},b)} {\partial w_j} = \frac 1 m \sum ^{m-1} _{i=0} (f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})x_j^{(i)} \\ \frac {\partial J(\vec{w},b)} {\partial b} = \frac 1 m \sum ^{m-1} _{i=0} (f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})
∂wj∂J(w,b)=m1i=0∑m−1(fw,b(x(i))−y(i))xj(i)∂b∂J(w,b)=m1i=0∑m−1(fw,b(x(i))−y(i))
推导公式
已知:
l
o
s
s
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
,
y
(
i
)
)
=
−
y
(
i
)
l
o
g
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
−
(
1
−
y
(
i
)
)
l
o
g
(
1
−
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
loss(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)}) = -y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)}))-(1-y^{(i)})log(1-f_{\vec{w},b}(\vec{x}^{(i)}))\\
loss(fw,b(x(i)),y(i))=−y(i)log(fw,b(x(i)))−(1−y(i))log(1−fw,b(x(i)))
J
(
w
⃗
,
b
)
=
1
m
∑
i
=
0
m
−
1
[
l
o
s
s
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
,
y
(
i
)
)
]
=
−
1
m
∑
i
=
1
m
−
1
[
(
y
(
i
)
l
o
g
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
+
(
1
−
y
(
i
)
)
l
o
g
(
1
−
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
)
]
J(\vec{w},b)=\frac 1 m \sum ^{m-1} _{i=0}[loss(f_{\vec{w},b}(\vec{x}^{(i)}),y^{(i)})] \\ =-\frac 1 m \sum ^{m-1} _{i=1}[(y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)}))+(1-y^{(i)})log(1-f_{\vec{w},b}(\vec{x}^{(i)})))]
J(w,b)=m1i=0∑m−1[loss(fw,b(x(i)),y(i))]=−m1i=1∑m−1[(y(i)log(fw,b(x(i)))+(1−y(i))log(1−fw,b(x(i))))]
对损失函数中第一项目
y
(
i
)
l
o
g
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)}))
y(i)log(fw,b(x(i))),根据求导法则,有:
∂
∂
w
j
(
y
(
i
)
l
o
g
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
)
=
y
(
i
)
f
w
⃗
,
b
(
x
⃗
(
i
)
)
∂
∂
w
j
(
f
w
⃗
,
b
(
x
(
i
)
)
)
\frac{\partial} {\partial w_j}(y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)})))= \frac {y^{(i)}} {f_{\vec{w},b}(\vec{x}^{(i)})} \frac {\partial} {\partial w_j}(f_{\vec{w},b}(x^{(i)}))
∂wj∂(y(i)log(fw,b(x(i))))=fw,b(x(i))y(i)∂wj∂(fw,b(x(i)))
f
w
⃗
,
b
(
x
(
i
)
)
=
1
1
+
e
w
⃗
x
⃗
+
b
f_{\vec{w},b}(x^{(i)})=\frac {1} {1+e^{\vec{w}\vec{x}+b}}
fw,b(x(i))=1+ewx+b1
∂
∂
w
j
(
f
w
⃗
,
b
(
x
(
i
)
)
)
=
∂
∂
w
j
u
(
−
1
)
=
−
u
(
−
2
)
∂
u
∂
w
j
=
−
1
(
1
+
e
w
⃗
x
⃗
+
b
)
2
∂
∂
w
j
(
1
+
e
w
⃗
x
⃗
+
b
)
=
.
.
.
\frac {\partial} {\partial w_j}(f_{\vec{w},b}(x^{(i)})) = \frac {\partial} {\partial w_j}u^{(-1)}=-u^{(-2)}\frac {\partial u} {\partial w_j}=-\frac {1} {(1+e^{\vec{w}\vec{x}+b})^2} \frac {\partial} {\partial w_j}(1+e^{\vec{w}\vec{x}+b})=...
∂wj∂(fw,b(x(i)))=∂wj∂u(−1)=−u(−2)∂wj∂u=−(1+ewx+b)21∂wj∂(1+ewx+b)=...
∂
∂
w
j
(
y
(
i
)
l
o
g
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
)
=
y
(
i
)
(
1
−
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
x
j
(
i
)
∂
∂
w
j
(
(
1
−
y
(
i
)
)
l
o
g
(
1
−
f
w
⃗
,
b
(
x
⃗
(
i
)
)
)
)
=
−
y
(
i
)
f
w
⃗
,
b
(
x
⃗
(
i
)
)
x
j
(
i
)
\frac{\partial} {\partial w_j}(y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)})))=y^{(i)}(1-f_{\vec{w},b}(\vec{x}^{(i)}))x_j^{(i)}\\ \frac{\partial} {\partial w_j}((1-y^{(i)})log(1-f_{\vec{w},b}(\vec{x}^{(i)})))=-y^{(i)}f_{\vec{w},b}(\vec{x}^{(i)})x_j^{(i)}
∂wj∂(y(i)log(fw,b(x(i))))=y(i)(1−fw,b(x(i)))xj(i)∂wj∂((1−y(i))log(1−fw,b(x(i))))=−y(i)fw,b(x(i))xj(i)
最终得到:
∂
J
(
w
⃗
,
b
)
∂
w
j
=
1
m
∑
i
=
0
m
−
1
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
∂
J
(
w
⃗
,
b
)
∂
b
=
1
m
∑
i
=
0
m
−
1
(
f
w
⃗
,
b
(
x
⃗
(
i
)
)
−
y
(
i
)
)
\frac {\partial J(\vec{w},b)} {\partial w_j} =\frac 1 m \sum ^{m-1} _{i=0} (f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})x_j^{(i)} \\ \frac {\partial J(\vec{w},b)} {\partial b} = \frac 1 m \sum ^{m-1} _{i=0} (f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})
∂wj∂J(w,b)=m1i=0∑m−1(fw,b(x(i))−y(i))xj(i)∂b∂J(w,b)=m1i=0∑m−1(fw,b(x(i))−y(i))
代码实现:
计算
∂
J
∂
w
j
\frac {\partial J} {\partial w_j}
∂wj∂J,
∂
J
∂
b
\frac {\partial J} {\partial b}
∂b∂J
def compute_gradient_logistic(X, y, w, b):
m,n = X.shape
dj_dw = np.zeros((n,))
dj_db = 0.
for i in range(m):
f_wb_i = sigmoid(np.dot(w,X[i]) + b)
err_i = f_wb_i - y[i]
dj_dw = dj_dw + err_i * X[i]
# for j in range(n):
# dj_dw[j] = dj_dw[j] + err_i * X[i,j]
dj_db = dj_db + err_i
dj_dw = dj_dw/m
dj_db = dj_db/m
return dj_db, dj_dw
梯度下降:
def gradient_descent(X, y, w_in, b_in, alpha, num_iters):
J_history = []
w = copy.deepcopy(w_in)
b = b_in
for i in range(num_iters):
dj_db, dj_dw = compute_gradient_logistic(X, y, w, b)
w = w - alpha * dj_dw
b = b - alpha * dj_db
if i<100000:
J_history.append( compute_cost_logistic(X, y, w, b) )
if i% math.ceil(num_iters / 10) == 0:
print(f"Iteration {i:4d}: Cost {J_history[-1]} ")
return w, b, J_history
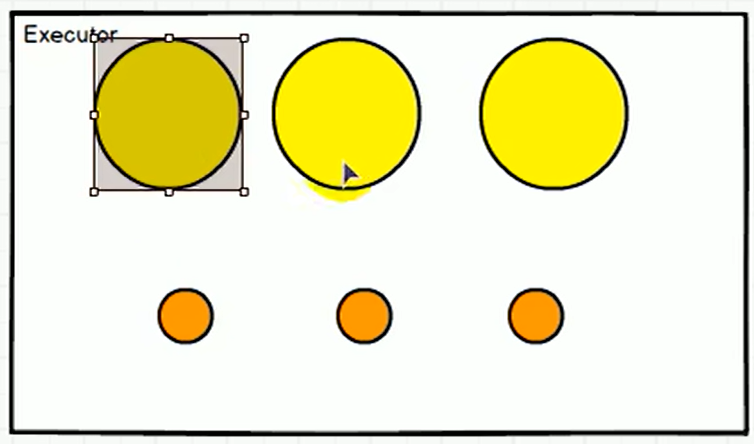
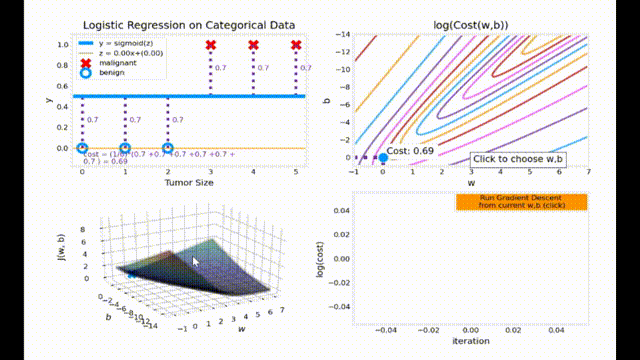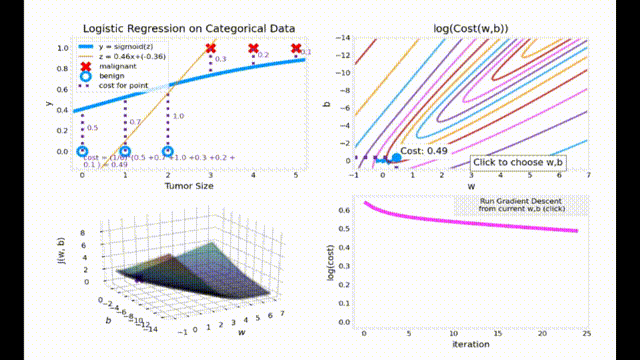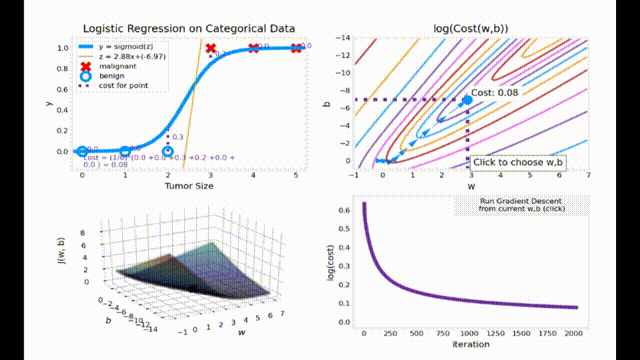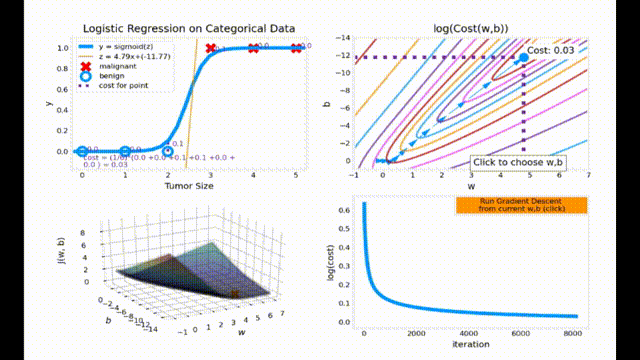
梯度下降动画效果展示
动画代码来源于 Ng. A. Machine Learning
Reference
Ng, A. (2017). Machine Learning [Coursera course]. Retrieved from https://www.coursera.org/learn/machine-learning/
Ng, A. (2017). Machine Learning [Coursera course]. Retrieved from https://www.coursera.org/learn/machine-learning/
Ng, A. (2017). Module 3: Gradient Descent Implementation [Video file]. Retrieved from https://www.coursera.org/learn/machine-learning/lecture/Ha1RP/gradient-descent-implementation