本章介绍正演的基础知识. 本贴的目的是进行内部培训, 错误之处较多, 希望不要误导读者.
2.1 弦线波动基本原理
波动方程是正演的基础.
最简单的模型是在一根弦上的波动, 假设如下:
- 横震动. 例如拨动吉他弦;
- 微小震动. 满足 u ( x + Δ x , t ) − u ( x , t ) ≪ Δ x u(x + \Delta x, t) - u(x, t) \ll \Delta x u(x+Δx,t)−u(x,t)≪Δx;
- 弦是柔软的. 张力沿着切线方向;
- 弦是均匀的. 密度均匀为 ρ \rho ρ.
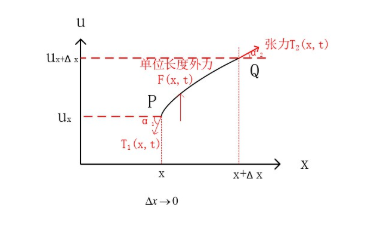
利用牛顿第二定律和上述假设条件可以推出一维非齐次波动方程的解:
∂
2
u
(
x
,
t
)
∂
t
2
=
c
2
∂
2
u
(
x
,
t
)
∂
x
2
+
f
(
x
,
t
)
(2.1)
\frac{\partial^2 u(x, t)}{\partial t^2} = c^2 \frac{\partial^2 u(x, t)}{\partial x^2} + f(x, t) \tag{2.1}
∂t2∂2u(x,t)=c2∂x2∂2u(x,t)+f(x,t)(2.1)
其中
c
2
=
T
/
ρ
c^2 = T / \rho
c2=T/ρ,
f
(
x
,
t
)
=
F
(
x
,
t
)
/
ρ
f(x, t) = F(x, t) / \rho
f(x,t)=F(x,t)/ρ.
进一步忽略重力
F
(
x
,
t
)
F(x, t)
F(x,t) 的作用, 可以推出一维齐次波动方程的解:
∂
2
u
(
x
,
t
)
∂
x
2
=
1
c
2
∂
2
u
(
x
,
t
)
∂
t
2
(2.2)
\frac{\partial^2 u(x, t)}{\partial x^2} = \frac{1}{c^2} \frac{\partial^2 u(x, t)}{\partial t^2} \tag{2.2}
∂x2∂2u(x,t)=c21∂t2∂2u(x,t)(2.2)
更多内容参见 弦线上的波动方程推导
疑问:
- T T T 是什么?
- 式 (2.1) 与 (2.2) 的物理意义是什么? 为什么要求二阶偏微分?
2.2 阻尼波动基本原理
阻尼标量波动方程
p
u
≡
∇
2
u
(
x
,
t
)
−
h
(
x
)
∂
2
u
(
x
,
t
)
∂
t
2
−
g
(
x
)
∂
u
(
x
,
t
)
∂
t
=
f
(
x
,
t
)
(2.1)
pu \equiv \nabla^2 u(x, t) - h(x) \frac{\partial^2 u(x, t)}{\partial t^2} - g(x) \frac{\partial u(x, t)}{\partial t} = f(x, t) \tag{2.1}
pu≡∇2u(x,t)−h(x)∂t2∂2u(x,t)−g(x)∂t∂u(x,t)=f(x,t)(2.1)
式中,
- u u u 表示地球物理场的一种, 如声场, 电磁场的某一分量等;
- f ( x , t ) f(x, t) f(x,t) 为源函数;
- x x x 为空间的一个点;
- t t t 为时间;
- 系数 h h h 和 g g g 对不同场有不同的物理意义.
2.2 有限差分法
2.1 波的分类
2.1.1 声波
2.1.2 弹性波
P波
S波