顺序表的定义

线性表的顺序存储又称顺序表。顺序表是在计算机内存中以数组的形式保存的线性表，线性表的顺序存储时指用一组地址连续的存储单元，依次存储线性表中的各个元素。因此线性表中任一数据元素都可以随机存取，所以线性表的顺序存储结构是一种随机存取的存储结构。

第一个元素存储在线性表的起始位置，数组下标为0，第i个元素存储在数组下标为i-1的位置。顺序表中元素的逻辑顺序与其物理顺序相同，且物理地址的相差为【数组下标的差 * sizeof(单个元素)】，例如：第一个数组的类型是char类型的数据，这个数组的第一个元素[下标为0]和第3个元素[下标为2]的物理地址相差为（2-0）* sizeof(char)。

一堆数组可以是静态分配的，也可以是动态分配的。在静态分配的时候，由于数组的大小和空间事先已经固定，一旦空间占满，再加入新的数据就会产生溢出，进而导致程序崩溃。在动态分配时，存储数组的空间是在程序执行过程中通过动态存储分配的，一旦数组空间占满，就另外开辟一块更大的存储空间，用以替换原来的存储空间，从而达到扩充存储数组空间的目的，而不需要为线性表一次性地划分所有空间。

顺序表的特点：

• 最主要的特点是随机访问，即通过首地址和元素序号可在时间O(1)内找到，即一次就可以找到。
• 存储密度高，每个结点只存储数据元素
• 逻辑上相邻的元素物理上也相邻，所以插入和删除操作需要移动大量的元素。

顺序表的基本操作

1）插入操作

逻辑：

• 判断插入的位置是否合法
• 判断顺序表是否满了，如果满了则不能插入
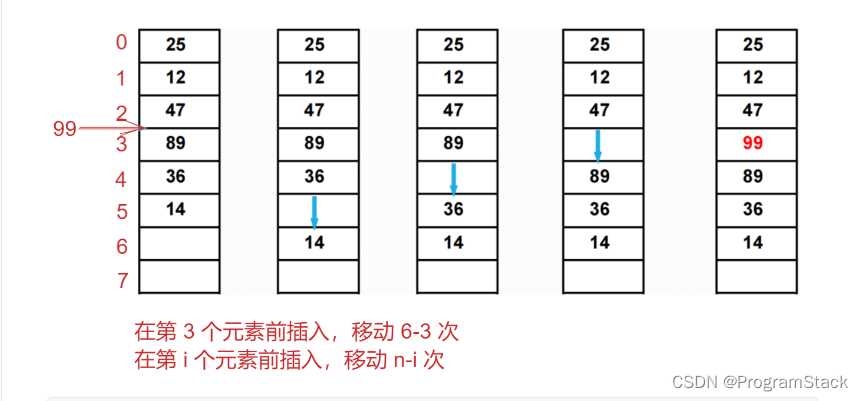
• 根据插入的位置计算需要移动的元素个数/次数
• 将指定位置开始的所有元素整体往后移动一个位置（从最后一个位置开始往后移动）
• 将需要插入的元素放置到插入的位置
• 顺序表长度+1

线性表的插入算法的平均时间复杂度为$O(n)$

# define ERROR 0
# define OK 1

typedef int ElemType;
typedef unsigned int uint;
typedef struct {
	ElemType *elem; //顺序表中存储数据的空间
    uint length;  //当前存储数据的个数
    uint listSize; //顺序表的容量
}SqList;

int elem_insert(SqList *t, uint index, ElemType elem)
{
    if (NULL == t)
    {
        printf("[%s %d] SqList is NULL\n", __FUNCTION__ , __LINE__);
        return ERROR;
    }
    //判断插入的位置是否合法
    if (index > t->length)
        return ERROR;

    //判断顺序表是否满了
    if (t->length == t->listSize)
        return ERROR;
    

    int i;
    for (i = 0; i < t->length - index; i++)
    {
        //从最后一个元素开始移动    t->elem[t->length+i] =  t->elem[t->length-1+i]
        t->elem[t->length+i] =  t->elem[t->length-1+i];
    }

    //将需要插入的元素放置到插入的位置
    t->elem[index] = elem;
    t->length++;

    return OK;
}

2）删除元素
逻辑：

• 遍历整个顺序表
• 判断遍历到得元素是否为需要删除的元素，如果不是则继续往后遍历
• 如果相等则将该元素后面得所有元素往前移动一个位置

删除元素的平均时间复杂度为$O(n)$

//删除元素

int delete_designated_elem(SqList *t, ElemType elem)
{
    if (NULL == t)
    {
        printf("[%s %d] SqList is NULL\n", __FUNCTION__ , __LINE__);
        return ERROR;
    }

    //元素遍历

    int i = 0;
    while (i != t->length)
    {
        //先找到需要删除的元素
        if (t->elem[i] != elem)
        {
            i++;
            continue;
        }
        //记录其位置
        int p = i;
        int j;
        //将后面的元素往前移动一个位置
        for (j = 0; j < t->length - (p + 1); j++)
        {
            //将 第 index + i + 1 个元素 覆盖掉 第 index + i个元素
            t->elem[p + j] = t->elem[p + j + 1];
        }
        t->length--;
    }
    return OK;
}