思维导图:

学习目标:
学习不定积分,我会采取以下几个步骤:
1.学习基本的积分表:首先,我会学习基本的积分公式,例如幂函数、指数函数、三角函数、反三角函数等的积分公式。这些公式是不定积分计算的基础,掌握它们是十分重要的。
2.理解积分的定义和性质:其次,我会学习积分的定义和基本性质,例如线性性、积分中值定理、换元积分法等。这些概念和性质是理解不定积分的基础。
3.多做练习:在掌握了基本积分公式和积分的定义和性质之后,我会多做一些练习题,以巩固所学知识。我会选择一些难度适中的练习题,不断提高自己的解题能力。
4.学习高级的积分技巧:在掌握了基本的积分技巧之后,我会学习一些高级的积分技巧,例如分部积分法、三角代换法、有理函数积分法等。这些技巧可以帮助我解决更复杂的积分问题。
5.学习应用:最后,我会学习不定积分在实际应用中的应用,例如面积、弧长、旋转体体积等。学习这些应用可以帮助我更好地理解不定积分的概念和性质,并且能够应用所学知识解决实际问题。
总之,学习不定积分需要建立在扎实的基础之上,需要掌握基本的积分公式和积分的定义和性质。在此基础之上,需要不断地做练习,提高自己的解题能力,并学习高级的积分技巧和应用。

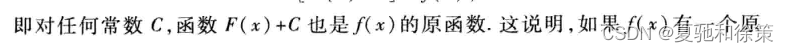





 我的理解:
我的理解:
原函数和不定积分是微积分中的两个重要概念,它们经常被一起提到,但并不完全相同。
-
原函数:一个函数f(x)的原函数,是指它的导函数F(x),即 f(x) = F'(x)。也就是说,如果对一个函数求导,得到的导数函数的反过来求导,就可以得到原来的函数。不过,原函数不是唯一的,因为在求导过程中,常数项会被忽略掉,所以任何两个不同的原函数只相差一个常数。
-
不定积分:给定一个函数f(x),它的不定积分是指所有的原函数构成的集合。表示为 ∫f(x) dx,其中 ∫ 代表积分符号,f(x) 为被积函数,dx 代表自变量x的微小增量。不定积分没有上下限,它的意义是求函数f(x)的所有原函数,因为原函数不是唯一的,所以不定积分结果一般会带上常数项。
需要注意的是,原函数和不定积分的概念是密切相关的,但并不完全相同。求解不定积分,其实就是在寻找一个函数的原函数。而对于同一个函数,它有多个不同的原函数,它们之间的关系是通过常数项联系在一起的。因此,在计算不定积分时,需要加上常数项,以表示不同的原函数。
在实际应用中,原函数和不定积分经常被用于求解曲线下的面积、求解物理学中的位移、速度、加速度等问题,它们是微积分中非常基础和重要的概念。



怎么记忆积分表:
记忆积分表需要一定的时间和精力,但是可以通过以下几个方法来加快记忆速度和提高效果:
-
理解积分公式的意义和应用场景。掌握积分公式的基本意义和应用场景,可以帮助记忆和应用积分公式。
-
将积分公式分类整理。积分公式有很多种,将其按照不同的类型分类整理,可以帮助记忆和区分各种积分公式。
-
经常练习和应用。积分公式的记忆需要经常的练习和应用,可以通过做题、模拟考试等方式,不断加深对积分公式的理解和记忆。
-
制作记忆卡片或手册。可以将积分公式写在卡片或手册上,方便随时查看和记忆。
-
利用联想和记忆法。可以将积分公式和一些易记的事物、图形、单词等进行联想和联系,形成印象深刻的记忆。
-
利用数学软件和工具。可以利用数学软件和工具来帮助记忆和应用积分公式,如Wolfram Alpha、Mathematica等。
总之,记忆积分表需要付出一定的时间和精力,但是通过科学有效的方法和不断的练习,可以提高记忆和应用积分公式的能力。





总结:
不定积分是微积分中的一个重要概念,是求解函数原函数的过程。下面是不定积分的概念及其性质的重点难点和易错点的总结:
概念:
- 不定积分可以理解为对函数进行反导的过程,即找到一个函数的导函数为给定的函数。
- 不定积分的符号为 ∫,下面没有上下限,表示对函数进行求和的过程。
- 不定积分的结果不唯一,因为一个函数的原函数可以加上任意常数而得到另一个原函数。
性质:
- 不定积分的线性性:对于任意实数 a,b,有 ∫(af(x) + bg(x))dx = a∫f(x)dx + b∫g(x)dx。
- 常数函数的不定积分为常数:∫kdx = kx + C。
- 幂函数的不定积分:∫x^n dx = (x^(n+1))/(n+1) + C,其中n不等于-1。
- 指数函数的不定积分:∫e^x dx = e^x + C。
- 对数函数的不定积分:∫1/x dx = ln|x| + C。
- 三角函数的不定积分:∫sin(x)dx = -cos(x) + C,∫cos(x)dx = sin(x) + C。
重点难点和易错点:
- 不定积分是求原函数,需要注意常数项的存在。
- 不同的函数可能有相同的导函数,但原函数可能不同。
- 在计算不定积分时,需要注意指数函数和对数函数的变化,避免遗漏常数项。
- 对于复杂的函数,可能需要使用分部积分法或换元积分法来求解不定积分。
总而言之,掌握不定积分的概念和性质,需要进行多次的练习和实践,注意理解和记忆重点难点和易错点,才能够熟练掌握不定积分的应用。