１、基本概念
dfs全称为Depth First Search,即深度优先搜索。它的思想是沿着每一条可能的路径一个节点一个节点地往下搜索,搜到了路径的到终点再回溯,一直到所有路径搜索完为止。
bfsbfs全称为Breath First Search,即广度(宽度)优先搜索。它的思想是将每一层的结搜素完成后在搜索下一层,一直到最后一层搜完为止。
２、搜索与遍历
通过遍历所有的可能情况，达到搜索的目的。
树的深度优先遍历和图的深度优先遍历
树的深度优先遍历已经很熟悉了，前中后序遍历，用递归或者栈都可以。
图的深度优先遍历
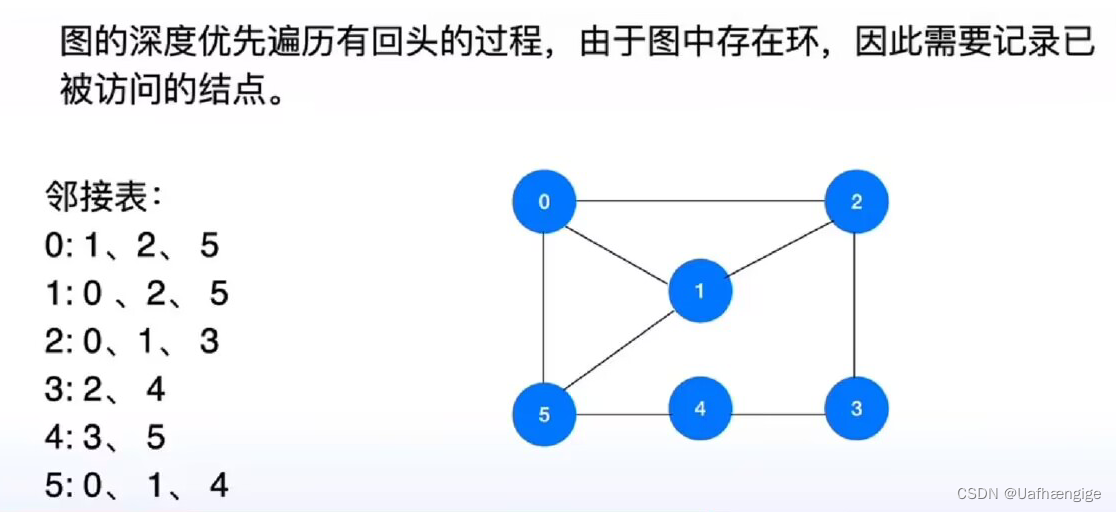
３、图的深度优先遍历基础
基本概念
图的定义
图(Graph)是由非空的顶点集合和一个描述顶点之间关系——边(或者弧)的集合组成，其形式化定义如下：
G=(V，E)
V={vi|vi∈dataObject}
E={(vi,vj)|vi,vj∈V∧P(vi,vj)}
其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合，集合E中P(vi,vj)表示顶点vi和顶点vj之间有一条直接连线，即偶对(vi,vj)表示一条边。
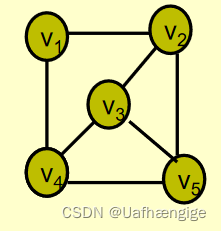
在这里插入图片描述
图G中：V(G)={v1,v2,v3,v4,v5}
E(G)={(v1,v2), (v1,v4), (v2,v3), (v2,v5),(v3,v4), (v3,v5), (v4,v5)}
在线性表中，元素个数可以为零，称为空表；
在树中，结点个数可以为零，称为空树；
在图中，顶点个数不能为零，但可以没有边。
顶点的度
依附于该顶点的边数，通常记为TD(v)。
顶点的入度
在有向图中，顶点v的入度是指以该顶点为弧头的弧的数目，记为ID(v)；
顶点的出度
在有向图中，顶点v的出度是指以该顶点为弧尾的弧的数目，记为OD(v)。
弧、弧头、弧尾
有向图的边称为弧。无向图叫做边。有序偶对<v，w>表示有向图从v到w的一条弧，v称为弧尾或始点，w称为弧头或终点
＜ｘ，ｙ＞表示从节点ｘ到节点ｙ
邻接矩阵
如图：说明ｖ１指向ｖ２， ｖ３，但是并不指向ｖ１，ｖ４
邻接表（用得多）
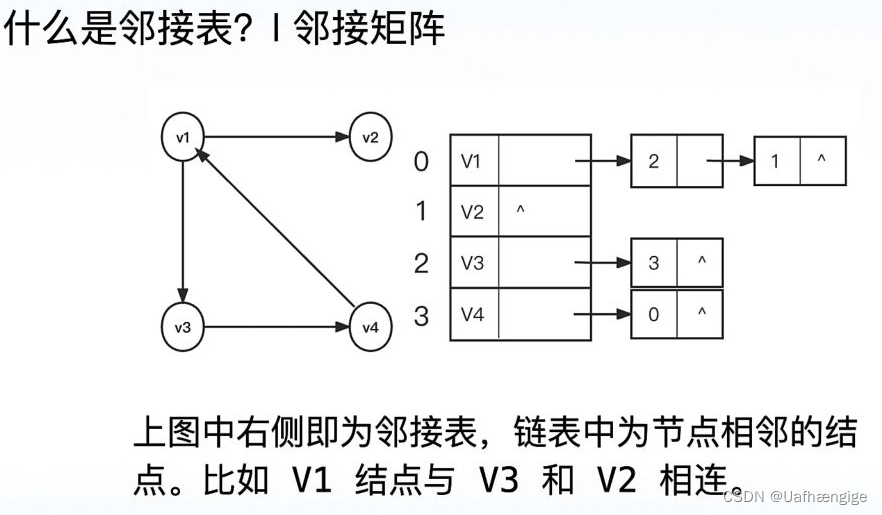邻接表有两种结点结构：顶点表结点和边表结点。
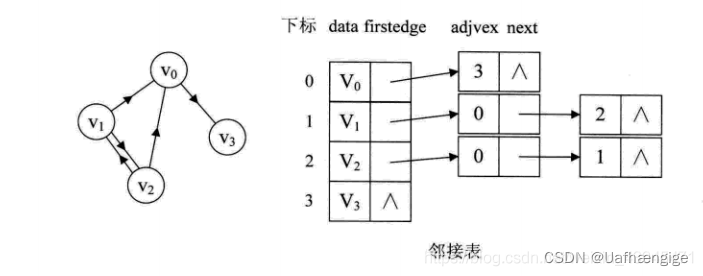
１、无向图：
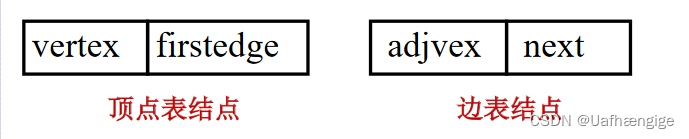
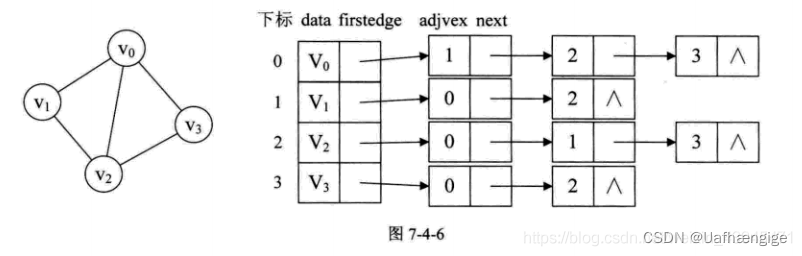从图中我们知道，顶点表的各个结点由data和 firstedge两个域表示，data是数据域，存储顶点的信息，firstedge是指针域，指向边表的第一个结点，即此顶点的第-一个邻接点。边表结点由adjvex 和 next两个域组成。adjvex是邻接点域，存储某顶点的邻接点在顶点表中的下标（是下标！！！），next则存储指向边表中下一个结点的指针。比如v顶点与vo、vz互为邻接点，则在v1的边表中，adjvex 分别为vo的0和v的2。
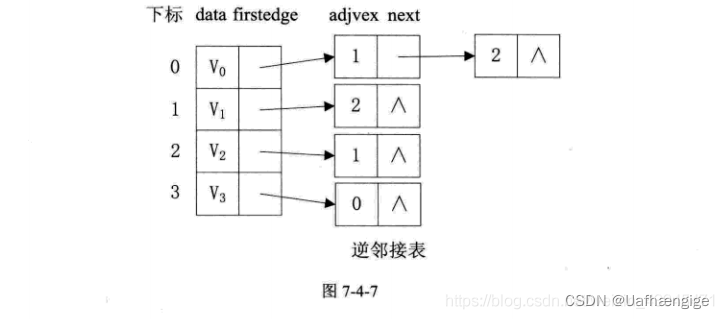
２、有向图
邻接表结构是类似的，比如图7-4-7中第一幅图的邻接表就是第二幅图。但要注意的是有向图由于有方向，我们是以顶点为弧尾来存储边表的，这样很容易就可以得到每个顶点的出度。但也有时为了便于确定顶点的入度或以顶点为弧头的弧，我们可以建立一个有向图的逆邻接表，即对每个顶点v都建立一个链接为v为弧头的表。如图7-4-7的第三幅图所示。
